LDA主题模型评估方法–Perplexity

在LDA主题模型之后，需要对模型的好坏进行评估，以此依据，判断改进的参数或者算法的建模能力。

Blei先生在论文《Latent Dirichlet Allocation》实验中用的是Perplexity值作为评判标准。

一、Perplexity定义

源于wiki：http://en.wikipedia.org/wiki/Perplexity

perplexity是一种信息理论的测量方法，b的perplexity值定义为基于b的熵的能量（b可以是一个概率分布，或者概率模型），通常用于概率模型的比较

wiki上列举了三种perplexity的计算：

1.1 概率分布的perplexity

公式：  

其中H(p)就是该概率分布的熵。当概率P的K平均分布的时候，带入上式可以得到P的perplexity值=K。

1.2 概率模型的perplexity

公式： 

公式中的Xi为测试局，可以是句子或者文本，N是测试集的大小（用来归一化），对于未知分布q，perplexity的值越小，说明模型越好。

指数部分也可以用交叉熵来计算，略过不表。

1.3单词的perplexity

perplexity经常用于语言模型的评估，物理意义是单词的编码大小。例如，如果在某个测试语句上，语言模型的perplexity值为2^190，说明该句子的编码需要190bits

二、如何对LDA建模的主题模型

Blei先生在论文里只列出了perplexity的计算公式，并没有做过多的解释。

在摸索过得知，M代表测试语料集的文本数量（即多少篇文本），Nd代表第d篇文本的大小（即单词的个数），P(Wd)代表文本的概率，文本的概率是怎么算出来的呢？

在解决这个问题的时候，看到rickjin这样解释的：

p(z)表示的是文本d在该主题z上的分布，应该是p(z|d)

这里有个误区需要注意：Blei是从每篇文本的角度来计算perplexity的，而rickjin是从单词的角度计算perplexity的，不要弄混了。

总结一下：

测试文本集中有M篇文本，对词袋模型里的任意一个单词w，P(w)=∑z p(z|d)*p(w|z)，即该词在所有主题分布值和该词所在文本的主题分布乘积。

模型的perplexity就是exp^{ – (∑log(p(w))) / (N) }，∑log(p(w))是对所有单词取log（直接相乘一般都转化成指数和对数的计算形式），N的测试集的单词数量（不排重）

评估LDA主题模型-perflexity

LDA主题模型好坏的评估，判断改进的参数或者算法的建模能力。

perplexity is only a crude measure, it's helpful (when using LDA) to get 'close' to the appropriate number of topics in a corpus. 

Blei先生在论文《Latent Dirichlet Allocation》实验中用的是Perplexity值作为评判标准，并在论文里只列出了perplexity的计算公式。

Note:M代表测试语料集的文本数量，Nd代表第d篇文本的大小（即单词的个数），P(Wd)代表文本的概率

文本的概率的计算：

p(z)表示的是文本d在该主题z上的分布，应该是p(z|d)

Note：

1. Blei是从每篇文本的角度来计算perplexity的，而上面是从单词的角度计算perplexity。

2. 测试文本集中有M篇文本，对词袋模型里的任意一个单词w，P(w)=∑z p(z|d)*p(w|z)，即该词在所有主题分布值和该词所在文本的主题分布乘积。

3. 模型的perplexity就是exp^{ - (∑log(p(w))) / (N) }，∑log(p(w))是对所有单词取log（直接相乘一般都转化成指数和对数的计算形式），N的测试集的单词数量（不排重）

4. P(w)=∑z p(z|d)*p(w|z)这个w是测试集上的词汇

[http://blog.csdn.net/pipisorry/article/details/42460023]

[http://faculty.cs.byu.edu/~ringger/CS601R/papers/Heinrich-GibbsLDA.pdf - 29页]

Estimate the perplexity within gensim

The `LdaModel.bound()` method computes a lower bound on perplexity, based on a supplied corpus (~of held-out documents).
This is the method used in Hoffman&Blei&Bach in their "Online Learning for LDA" NIPS article.

[https://groups.google.com/forum/#!topic/gensim/LM619SB57zM]

you can also use model.log_perplexity(heldout), which is a convenience wrapper.

[Questions find in : the mailing list of gensim]

皮皮blog

评价一个语言模型Evaluating Language

假设我们有一些测试数据，test data.测试数据中有m个句子;s1,s2,s3…,sm

我们可以查看在某个模型下面的概率：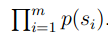

我们也知道，如果计算相乘是非常麻烦的，可以在此基础上，以另一种形式来计算模型的好坏程度。

在相乘的基础上，运用Log，来把乘法转换成加法来计算。

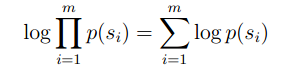
补充一下，在这里的p(Si)其实就等于我们前面所介绍的q(the|*,*)*q(dog|*,the)*q(…)…

有了上面的式子，评价一个模型是否好坏的原理在于：

a good model should assign as high probability as possible to these test data sentences.

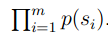,this value as being a measure of how well the alleviate to make sth less painful or difficult to deal with language model predict these test data sentences.

The higher the better.

上面的意思也就是说，如果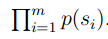的值越大，那么这个模型就越好。

• 实际上，普遍的评价的指标是perplexity

其中，M的值是测试数据test data中的所有的数量。

那么从公式当中查看，可以知道。perplexity的值越小越好。

为了更好的理解perplexity，看下面这个例子：

• 我们现在有一个单词集V，N=|V|+1

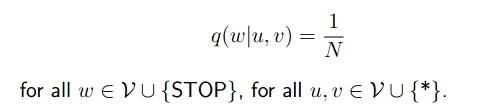
有了上面的条件，可以很容易的计算出：

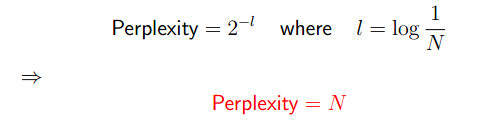
Perplexity是测试branching factor的数值。

branching factor又是什么呢？有的翻译为分叉率。如果branching factor高，计算起来代价会越大。也可以理解成，分叉率越高，可能性就越多，需要计算的量就越大。

上面的例子q=1/N只是一个举例，再看看下面这些真实的数据：

• Goodman的结果，其中|V|=50000，在trigram model的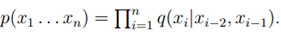中，Perplexity=74
• 在bigram model中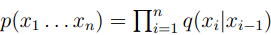，，Perplexity=137
• 在unigram model中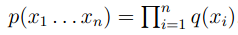，，perplexity=955

在这里也看到了，几个模型的perplexity的值是不同的，这也就表明了三元模型一般是性能良好的。

[评价一个语言模型Evaluating Language Models:Perplexity]

皮皮blog

Topic Coherence

一种可能更好的主题模型评价标准

[Optimizing semantic coherence in topic models.]

from:http://blog.csdn.net/pipisorry/article/details/42460023

ref:Topic models evaluation in Gensim

http://stackoverflow.com/questions/19615951/topic-models-evaluation-in-gensim

http://www.52ml.net/14623.html

Ngram model and perplexity in NLTK

http://www.researchgate.net/publication/221484800_Improving_language_model_perplexity_and_recognition_accuracy_for_medical_dictations_via_within-domain_interpolation_with_literal_and_semi-literal_corpora

Investigating the relationship between language model perplexity and IR precision-recall measures.

LDA/NMF/LSA多模型/多主题一致性评价方法《Exploring topic coherence over many models and many topics》K Stevens, P Kegelmeyer, D Andrzejewski... [University of California Los Angeles] (2012)  GITHUB

论文:(概率)生成模型评价方法研究《A note on the evaluation of generative models》Lucas Theis, Aäron van den Oord, Matthias Bethge (2015)

Notes on A note on the evaluation of generative models by Hugo Larochelle