[注：这一节是在学习东南大学廖力老师的公开课时，所记录的一些知识点截屏，谢谢廖力老师的辛劳付出]

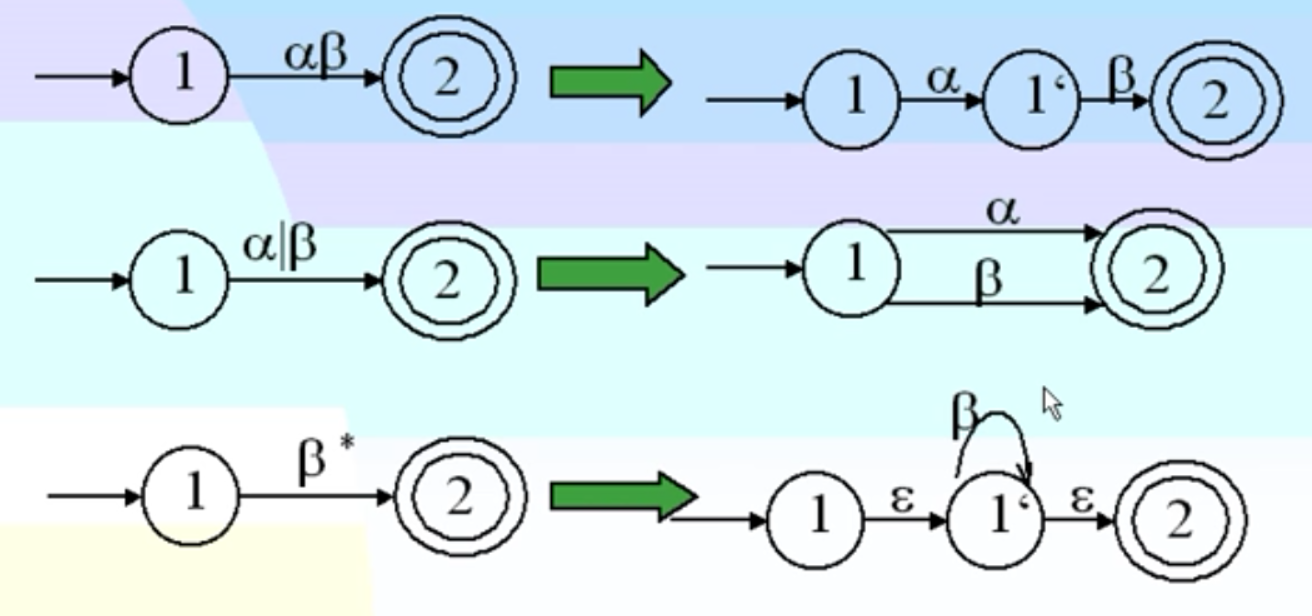
引入3条正规式分裂规则来分裂α，所得到的是NFA  M（因为包含ε弧，之后进行确定化就是所需要求得DFA）：

对含有ε弧的NFA进行确定化（）采用子集法,含有ε边的状态，将直接加入进子状态,如下图中，初态x，经由ε弧可直接到达5,1，所以初态集变更为{x,5,1}

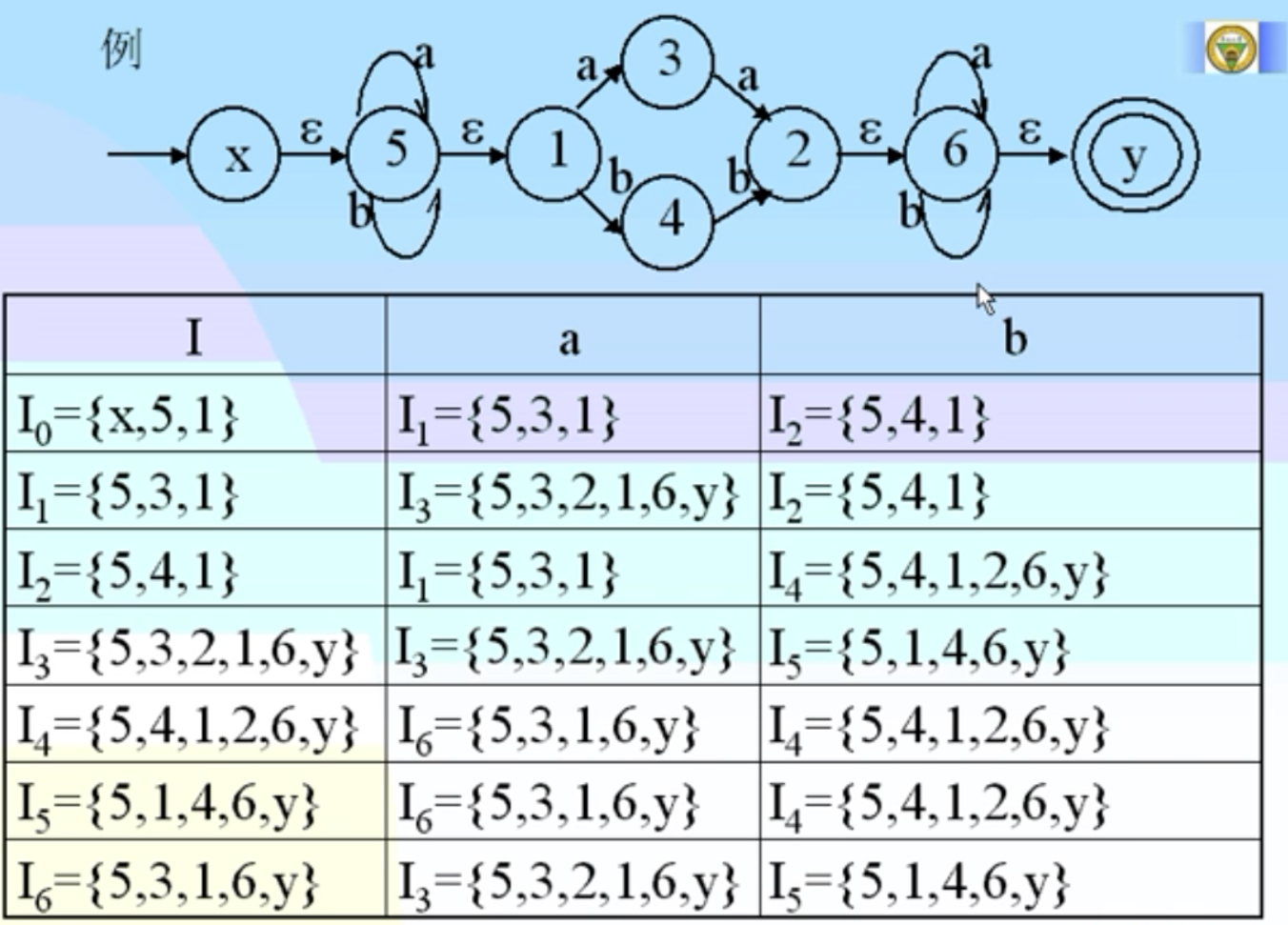
接下来就是按表构造DFA接着化简了，具体方法可以跳转到

如何将不确定的有穷自动机确定化，并将其化简为最简DFA

正规式α向有限自动机M的转换的更多相关文章

  1. 正规表达式与有限自动机和LEX

    正规式与有限自动机的等价性 一个正规式r与一个有限自动机M等价, L(r)=L(M) FA ->正规式,对任何FA M,都存在一个正规式r,使得L(r)=L(M). 正规式 -> FA, ...

  2. 自动构造词法分析器的步骤——正规式转换为最小化DFA

    正规式-->最小化DFA 1.先把正则式-->NFA(非确定有穷自动机) 涉及一系列分解规则 2.再把NFA通过"子集构造法"-->DFA 通过子集构造法将NFA ...

  3. 编译原理：正规式转变成DFA算法

    //将正规式转变成NFApackage hjzgg.formal_ceremony_to_dfa; import java.util.ArrayList; class Edge{ public int ...

  4. 正规式->最小化DFA说明

      整体的步骤是三步: 一,先把正规式转换为NFA(非确定有穷自动机), 二,在把NFA通过"子集构造法"转化为DFA, 三,在把DFA通过"分割法"进行最小化 ...

  5. 《编译原理》构造与正规式 (0|1)*01 等价的 DFA - 例题解析

    <编译原理>构造与正规式 (0|1)*01 等价的 DFA - 例题解析 解题步骤: NFA 状态转换图 子集法 DFA 的状态转换矩阵 DFA 的状态转图 解: 已给正规式:(0|1)* ...

  6. 正规式与正规集，DFA与NFA

    词法分析器的设计 词法分析器的功能:输入源程序.输出单词符号 词法分析器的设计:给出程序设计语言的单词规范--单词表, 对照单词表设计识别该语言所有单词的状态转换图, 根据状态转换图编写词法分析程序 ...

  7. 编译原理课后习题答案令A,B和C是任意正规式,证明以下关系成立(A|B)*=(A*B*)*=(A*|B*)*

    题目: 令A.B和C是任意正规式,证明以下关系成立: A∣A=A (A*)*= A*         A*=ε∣A A*        (AB)*A=A(BA)*        (A∣B)*=(A*B ...

  8. 有穷自动机（NFA、DFA）&正规文法&正规式之间的相互转化构造方法

    在编译原理(第三版清华大学出版社出版)中第三章的词法分析中,3.4.3.5.3.6小节中分别讲解了 1.什么是NFA(不确定的有穷自动机)和DFA(确定的有穷自动机) 2.如何将  不确定的有穷自动机 ...

  9. 学习响应式编程 Reactor (4) - reactor 转换类操作符（1）

    Reactor 操作符 数据在响应式流中的处理,就像流过一条装配流水线.Reactor 既是传送带,又是一个个的装配工或机器人.原材料从源头(最初的 Publisher )流出,经过一个个的装配线中装 ...

随机推荐

  1. 六、SpringBoot配置@ConfigurationProperties与@Value区别

    1.@Value的使用 三种用法 // ${key} 从环境变量.配置文件中取值 @Value("${person.last-name}") private String last ...

  2. poj 1144 割点模板题

    题目大意: 求割点: 基本思路: tarjan算法,套板子 代码如下: #include<iostream> #include<string> #include<vect ...

  3. maven打包出现 Error assembling JAR: java.lang.reflect.InvocationTargetException

    如果项目的包名使用中文,会反射找不到,idea设置Editor->File Encodings 改utf-8试试

  4. 4K超清，2500万人在线，猫晚直播技术全解读

    摘要: 作为双11的必备节目,今年的猫晚通过优酷.浙江卫视.东方卫视进行了全程网络直播和电视直播,吸引了超过全球超过2.4亿人收看.猫晚期间,优酷基于阿里云最新的广播级高可靠直播方案,为近2500万的 ...

  5. qt学习（三）：鼠标图标改变

    qt学习 (三):鼠标图标改变 当你进入一个美好的qt软件场景,比如游戏,电脑的黑白图标会让程序逊色不少, 1改图标要加光标的头文件, 2 载入光标图, 3 再设置改光标就可以了 1在头文件中加 #i ...

  6. 【Beta阶段】第十一次Scrum Meeting!

    第十一周会议记录 [Beta阶段]第十一次Scrum Meeting! 一.每日任务内容 本次会议为第十一次Scrum Meeting会议~ 本次会议主要探讨了各自进展以及后续要继续开展的工作. 小组 ...

  7. [NOIP模拟测试38]题解

    来自达哥的问候…… A.金 显然本题的考察点在于高精而不是裴蜀定理 根据裴蜀定理易得答案为Yes当且仅当$gcd(n,m)=1$,那么考虑怎么在高精度下判互质. 如果$n,m$都能被2整除,那么显然不 ...

  8. (61)C# 可枚举类型和迭代器

    一.可枚举类型 枚举器-Enumerator  是一个只读且只能在值序列向前移动的游标 枚举器需要实现下列接口之一 System.Collections.IEnumerator System.Coll ...

  9. RHEL6.1 安装 Oracle10gr2 (图文、解析)

    目录 目录 软件环境 前言 初始化RHEL61 硬件检测 预安装软件包 安装oratoolkit 创建Oracle用户 修改配置文件 系统版本伪装 解压并运行Oracle10gr2安装包 安装rlwr ...

  10. P3203 [HNOI2010]弹飞绵羊(LCT)

    弹飞绵羊 题目传送门 解题思路 LCT. 将每个节点的权值设为\(1\),连接\(i\)和\(i+ki\),被弹飞就连上\(n\),维护权值和\(sum[]\).从\(j\)弹飞需要的次数就是\(sp ...