【统计】Causal Inference

【统计】Causal Inference

原文传送门

http://www.stat.cmu.edu/~larry/=sml/Causation.pdf

过程

一、Prediction 和 causation 的区别

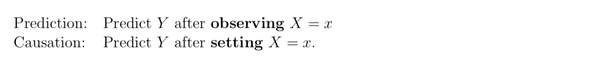
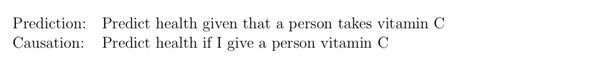
现实中遇到的很多问题实际上是因果问题，而不是预测。

因果问题分为两种：一种是 causal inference，比如给定两个变量 X、Y，希望找到一个衡量它们之间因果关系的参数 theta；另一种是 causal discovery，即给定一组变量，找到他们之间的因果关系。对于后面这种 causal discovery，notes 里面说它在统计上是不可能的。

数据有两种产生途径：一种是通过有意控制、随机化的实验得到的；一种是通过观测数据得到的。前一种方式能够直接做 causal inference；后一种方式需要另外知道一些先验知识，才能在上面做 causal inference。

对因果关系描述的数学语言：一种是 counterfactuals，一种是 causal graph；还有一种和 causal graph 相近的 structural equation models。

Correlation is not causation

预测问题可以写为

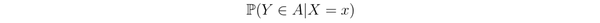
它表示的是，如果我们观察到 X=x，预测 Y。而因果推断关系的是

它表示我们如果把某个变量 X 设置为 x，那么 Y 会是多少。数学上表示出来就是

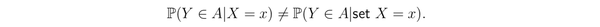
一个简单的例子『睡眠超过 7 小时的人』（X）『生病少』（Y)，只是代表 X 和 Y 之间有关联性，并不代表如果强制一个人睡眠超过 7 小时，ta 就能够生病少。因为可能『身体好的人』容易『睡眠超过 7 小时』，同时 ta 也『生病少』；但是一个本来身体不好的人，强制 ta 睡眠多，ta 可能也生病不会少。

Notes 里面想要说明的结论是：因果关系可以从随机化的实验中得到；但是很难从观察到的数据中得到。

另外一个例子说明 correlation 和 causation 的区别

考虑数据是由一段程序生成的：

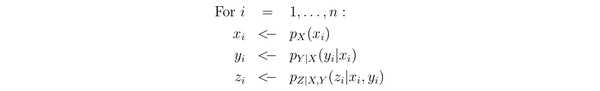
估计 correlation 时，我们会统计 Z=z & Y=y 的样本占 Y=y 样本的多大比例，它等价于

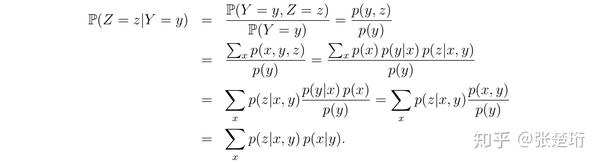
当我们研究因果关系的时候，我们是想知道，如果『设置』Y=y，会怎样引起 Z 的分布；该过程可以用如下程序模拟

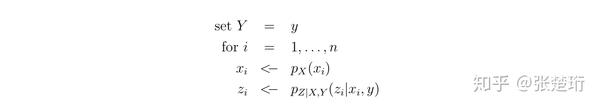
在这种情况下，我们再统计 Z=z 占总体样本的比例，即

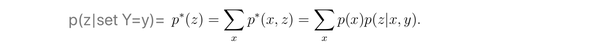
二、Counterfactuals

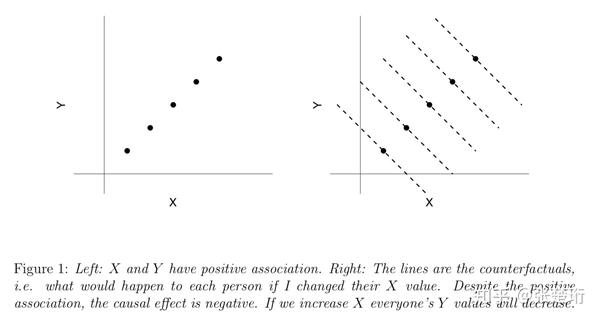
考虑一个 treatment X，和一个 outcome Y。我们能观察到的是一些数据 ，但是我们无法知道如果对于某一个数据点 ，如果改变 X 的值，Y 会怎么变。这件事情就叫做 counterfactual。Notes 里面给了一个图（下图），从数据上看，X 和 Y 是正相关的，但其实对于每一个 样本来说，如果增大 X，会引起 Y 的减小。这一点最开始看的时候并不好理解。举一个例子。研究航空公司票价（X）对销量（Y）的影响，显然，对于某一个客户来说，增加票价（X 变大）会降低客户购买意愿，即使得销量将达（Y 变小）。但是实际中的情况是，在节假日人们出行意愿大导致销量高（Y 大），定价也会相应变高（X 大），从而从数据上看，形成左边图的情形。

假设 X 取值 0 或者 1，Y 也取值 0 或者 1。引入变量 ，认为

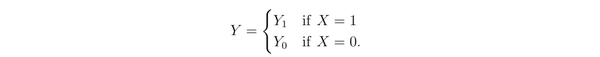
这两个变量也叫做 potential outcome 或者 counterfactuals，因为如果在数据中观察到 X=0，就只能观察到 ，而此时的 就没法观察到了。比如，一个观察到的数据集长这样：

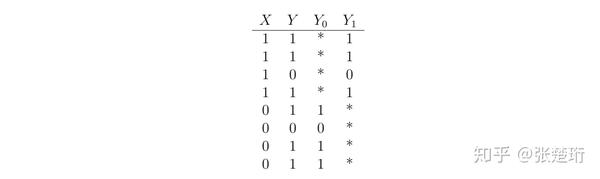
而我们关心的 ， 。而由于这些未知的 * 的存在，使得我们没有办法估计到它们。但是，显然有

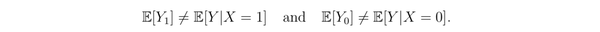
定义

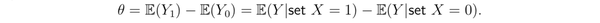
为 mean treatment effect，它可以被看做是一个衡量因果关系的参数；如果它大于零，表示我们设置 X=1 会在期望上增大 Y（这是一个因果推断）。

文章下面给出了一个定理，说明不可能从数据里面估计出 。

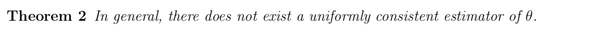
其中 uniformly consistent estimator 的定义是

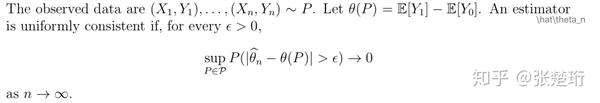
其实这很好理解，可以构造两个数据集，它们有不同的 分布，使得它们 不同，但是形成的数据 是一样的。这可以通过任意设置前面例子中的 * 来实现。

那么应该如何估计 呢？下面介绍两种方法：一种方法就是使用 randomization，另一种方法叫做 adjusting for confounding。

三、用随机化来估计因果关系

如果我们能够随机设定 X 的值，使得 X 和 相互独立，就能有办法估计 ，即

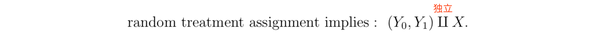
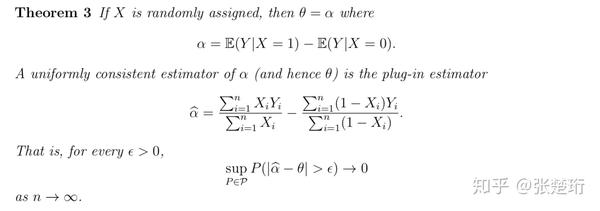
可以这么做最主要的原因就是当 X 和 相互独立时， ，因此， ，即

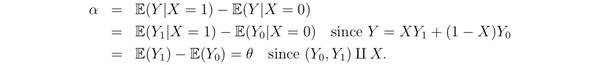
总结来说，在完全随机的情况下（X 和 相互独立），correlation=causation。

【注】Randomization 并不意味着 X 的选取要是 uniformly random（比如一半选 0，一半选 1），可以令 X 为任意分布，只要它和 相互独立即可。

四、Adjusting for Confounders

有些时候我们没法做实验，只能从可以观察的数据中来估计。比如，研究抽烟（X）和肺癌（Y）之间的因果关系，不可能故意选人去让他抽烟或者不抽烟。那么应该如何找到其中的因果关系呢？

Causal inference in observational studies is not possible without subject matter knowledge

注意到，观察到的数据中不能假设 X 和 相互独立。这里考虑一个例子，服用 VC（X）对于健康与否（Y）的关系。一个健康的人不论吃不吃 VC，理应都是健康的，但是健康的人喜欢吃 VC；一个不健康的人无论吃不吃 VC，他都不健康。因此，我们可能观察到如下数据（X=1 表示吃 VC，Y=1 表示健康）。

因此，实际情况是吃 VC 和健康之间没有因果关系，即 ；但是从数据中的估计来看，这二者之间有很强的关联，即 。

Use confounding variables

虽然在数据中 X 和 不相互独立，但是如果我们能够找到共同影响 X 和 Y 的因素，并把它通过某种统计方式排除的话，也可以可以做因果推断的。这里的共同因素就是 confounding variables Z，即希望找到一个 ，使得 there is no unmeasured confoundings or ignorability holds。

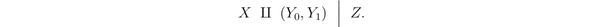
下面的定理就是说，如果 能够观察到这样的 confounding variable，那么也能够做因果推断。

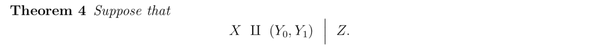
证明过程也比较好理解，因为在 Z 给定之后 X 和 是相互独立的（箭头标注的那一步）。

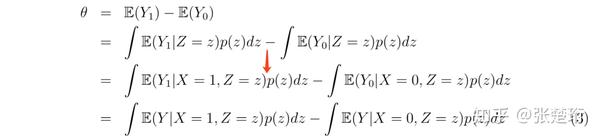
这个方法叫做 adjusting for confounders，同时也把这上面的 叫做 adjusted treatment effect。

Intuitive 地来说，拿航空公司票价（X）和销量（Y）的例子来说，它们可能受到节假日（Z）的影响，节假日的时候（Z=1）票价高，销量也大。要搞清楚其中的因果关系，就需要分别在是节假日（Z=1）和非节假日的时候（Z=0）统计 X、Y 的关系。

The usual bias-variance tradeoff does not apply

Notes 里面提到，在估计 的时候要特别小心，在因果推断里面 bias 的危害会更大，因此拟合的时候会尽量更『平滑』。这一块有特别的一些方法来解决该问题，叫 semiparametric inference 以及后面会讲的 matching。

对于前面这个离散的例子来说，可以对 做线性拟合，即 。我们可以看到，这种情况下，线性回归中 x 前面的系数就代表了 x 的 causal effect。

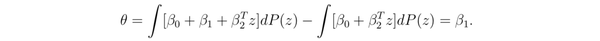
对于连续的情形类似地，有

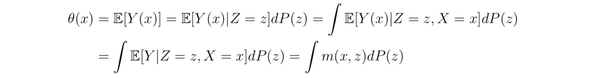
总结：如果 1）线性模型正确；2）所有的 confounding variables 都包含到回归方程中了，那么 x 前面的系数就表示 x 的 causal effect。

五、Causal Graphs

Causal graph 是一个有向无环图（DAG），表明了各个变量之间的联合概率分布

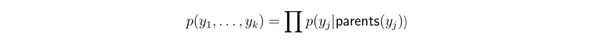
下面举例说明，在给定一个 causal graph 之后，如何做因果推断。考虑下面一个 causal graph，目标是求 。

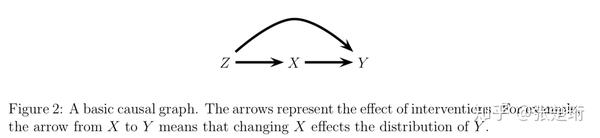
首先，可以看出该 causal graph 提供的信息为 。

接下来，由于考虑的是设定 X 的数值的影响，因此构建一个新图 ，移除掉所有指向 X 的边，得到新的联合概率分布 。

最后，该概率分布下的数值就是因果推断的结果

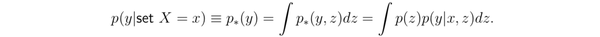
在 情形下，

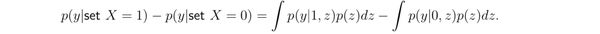
和 adjusting for confounder 方法的等价性

比如还是在 情形下，从上述方法出发计算

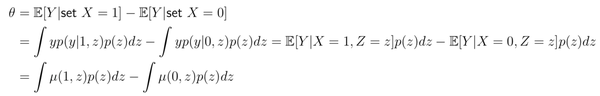
其结果和 adjusting for confounder 方法一致。

和 randomized experiment 方法的等价性

当 X 的选取是随机时，就没有从 Z 到 X 的箭头了，因此直接在概率图上计算可以得到 ，和这里得到的一致。

Causal graph 和 probability graph 的区别

举例说明，比如下雨（Rain，R）和湿草坪（Wet Lawn，W）是不相互独立的， 即 。

对于下两种 DAG，它们都是合理的 probability graph，即对于任意的联合概率分布 ，都可以写成 或者 。但显然下雨是因、草坪湿是果，只有左边的图才是正确的 causal graph。

分析 ，按照应该关系，把草坪弄湿不会影响是否下雨。对左边的图推断 ，先把指向 W 的边去掉，形成如下图

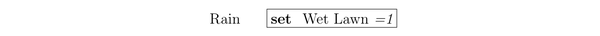
因此得到 ，由此得出结论 ，即草坪弄湿不引起下雨。

六、Causal Discovery 是不可能的

下面想说明的是在不做 randomized experiment 并且也观察不到所有 confounders 时，研究两个变量之间是否有因果关系是不可能的。

考虑一个最简单的情形，就是研究『 X 是否引起 Y（X、Y 之间是否有因果关系）』；同时能够肯定地排除掉『Y 引起 X 』的情形（比如，时间先后关系，发生在后面的不可能引起发生在前面的）。考虑可能的 confounding variable U，它们之间可能的关系有如下八种。

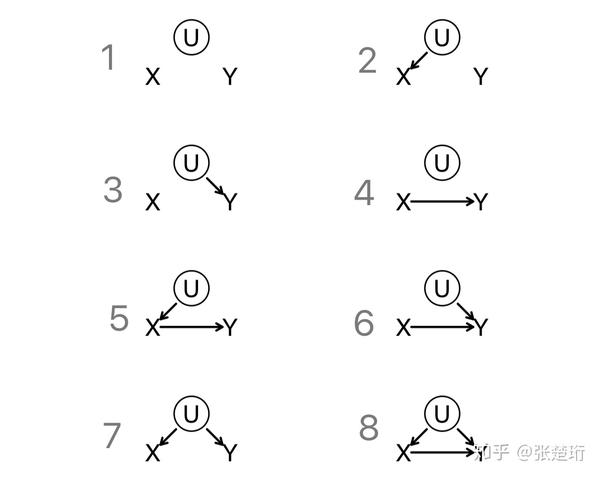
如果我们只能观察到 X、Y 的数据，能做的是估计 。如果 说明 X、Y 之间有关联，因此可能的情况是 4-8，这里面有些情况下 X->Y，有些是没有，因此无法得出什么有效的结论；如果 ，基本上锁定是 1-3 中的情况，我们发现这三种情况中 X 都不引起 Y，于是我们能得出结论 X 和 Y 之间没有因果关系。这是错的！

情况 8 也能够引起 ！比如 X->Y 的影响可能会被 U->Y 的影响抵消，这称作 unfaithfulness，这样的情形记做 。举一个粗俗的例子，比如情况 8 中的关系都是确定性的，Y|U = -U, Y|X,U = X+U，于是乎，按照这样的模型生成的 Y 全部等于零，显然估计出来的 。

因此，要想得出结论得出结论 X 和 Y 之间没有因果关系，还必须限定 faithfulness。

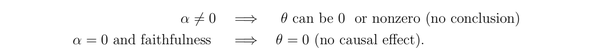
Notes 后面还讲了，总存在一个 faithful 的分布使得在样本足够多的时候，产生足够大的 type I error。