05-转置-置换-向量空间R

一、置换矩阵

　一个矩阵的行或者列交换，可以借助另外一个矩阵相乘来实现

　首先是行交换：

$\underbrace{\left[\begin{array}{ccc}{1} & {1} & {1} \\ {2} & {2} & {2} \\ {3} & {3} & {3}\end{array}\right]}_{A} \stackrel{S_{12}}{\rightarrow} \underbrace{\left[\begin{array}{ccc}{2} & {2} & {2} \\ {1} & {1} & {1} \\ {3} & {3} & {3}\end{array}\right]}_{A_{2}}$

也就是矩阵的第一行和第二行进行了互换

　　对于$A_2$的第一行，相当于从$A$中拿出了0个第一行，1个第二行，0个第三行进行加和

　　对于$A_2$的第二行，相当于从$A$中拿出了1个第一行，0个第二行，0个第三行进行加和

　　对于$A_2$的第三行，相当于从$A$中拿出了0个第一行，0个第二行，1个第三行进行加和

　　之前我们讲过，行向量乘以一个矩阵，结果等于矩阵的每行的线性组合

　　上面的$P_{12}$称为行置换矩阵。可以看出置换矩阵是行重新排列了的单位矩阵，它的一个特性是：$\mathrm{P}^{-1}=\mathrm{P}^{\mathrm{T}}$

　列交换与行交换类似，但是向量变为右变列向量（左行右列就是这个意思）

$\underbrace{\left[\begin{array}{lll}{1} & {2} & {3} \\ {1} & {2} & {3} \\ {1} & {2} & {3}\end{array}\right]}_{A} \stackrel{C_{12}}{\longrightarrow} \underbrace{\left[\begin{array}{ccc}{2} & {1} & {3} \\ {2} & {1} & {3} \\ {2} & {1} & {3}\end{array}\right]}_{A_{2}}$

也就是矩阵的第一列和第二列进行了互换

　　对于$A_2$的第一列，相当于从$A$中拿出了0个第一列，1个第二列，0个第三列进行加和

　　对于$A_2$的第二列，相当于从$A$中拿出了1个第一列，0个第二列，0个第三列进行加和

　　对于$A_2$的第三列，相当于从$A$中拿出了0个第一列，0个第二列，1个第三列进行加和

　　之前我们已经讲过：矩阵乘以一个列向量，得到一个列向量-也就是原矩阵得各列得线性组合

　　上面得$C_{12}$称为列置换矩阵。注意列置换矩阵的结果，是按照列构成的

　总结：置换矩阵就是行或者列重新排列了的单位矩阵，置换矩阵可以用在消元过程中防止主元为0

二、转置矩阵

　即原始矩阵得行变成列，列变成行，用$A^T$表示：

$\left[\begin{array}{ll}{1} & {1} \\ {4} & {5} \\ {0} & {3}\end{array}\right]$的转置是$\left[\begin{array}{lll}{1} & {4} & {0} \\ {1} & {5} & {3}\end{array}\right]$

　注：一个矩阵与转置矩阵相乘可以得到对称矩阵，证明如下

　$(R^TR)^T = R^T(R^T)^T=R^TR$，所以一个矩阵$R^TR$的转置与自身相等，那么他就是对称的

 

三、向量空间

　向量有两个最基本的运算：相加$v_a + v_b$和数乘$num * v$

　$R^2$是个二维的向量空间，$R^3$是个三维的向量空间，是所有三维向量组成的向量空间，同理$R^n$是所有$n$维向量组成的向量空间

　所有向量空间必须包含0向量

　我们从$R^2$出发，取二维坐标系的第一象限，那么该区域是向量空间吗？显然不是，因为该区域的向量乘以一个负数的话就跑出该区域空间了，不在该区域内了，所以第一象限显然不是一个向量空间

　那么既然第一象限不是一个向量空间，$R^2$向量空间内是否存在其他向量空间呢（其实也叫向量子空间）？当然存在，如$R^2$向量空间内过原点的某条直线

　　由于该直线过原点，所以该直线上的任意一个向量进行数乘或者该直线上的任意向量进行相加，结果仍然落在该直线上，所以该直线就是$R^2$向量空间的子空间

　　但要注意并不是所有直线都是$R^2$向量空间的子空间，比如某条直线如果不过原点，那么该直线上的向量数乘0之后结果为0向量，0向量则不在该直线上，所以该不过原点的直线不是$R^2$向量空间的子空间

　既然讲了$R^2$向量空间，那么其子空间有哪些呢？

　　a）其$R^2$本身，即整个$R^2$向量空间

　　b）直线：确切的说是穿过0点的直线

　　c）点：即0点，通常记为$Z$

　同理，$R^3$向量空间，那么其子空间有哪些呢？

　　a）其$R^3$本身，即整个$R^3$向量空间

　　b）平面：确切的说是穿过0点的平面

　　c）直线：确切的说是穿过0点的直线

　　d）点：即0点，通常记为$Z$

　下面我们来看看矩阵是如何构成子空间的，也就是我们从一个矩阵构造出子空间：

　　1）通过列向量来构造，如

$A=\left[\begin{array}{ll}{1} & {3} \\ {2} & {3} \\ {4} & {1}\end{array}\right]$各列属于$R^3$

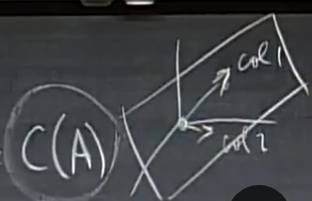
我们想用其各列来构成$R^3$的子空间：方法就是矩阵各列的线性组合，记作$C(A)$，C代表列空间

针对上面的矩阵$A$，其列空间就是穿过各列和原点的平面