核型SVM

（本文内容和图片来自林轩田老师《机器学习技法》）

1. 核技巧引入

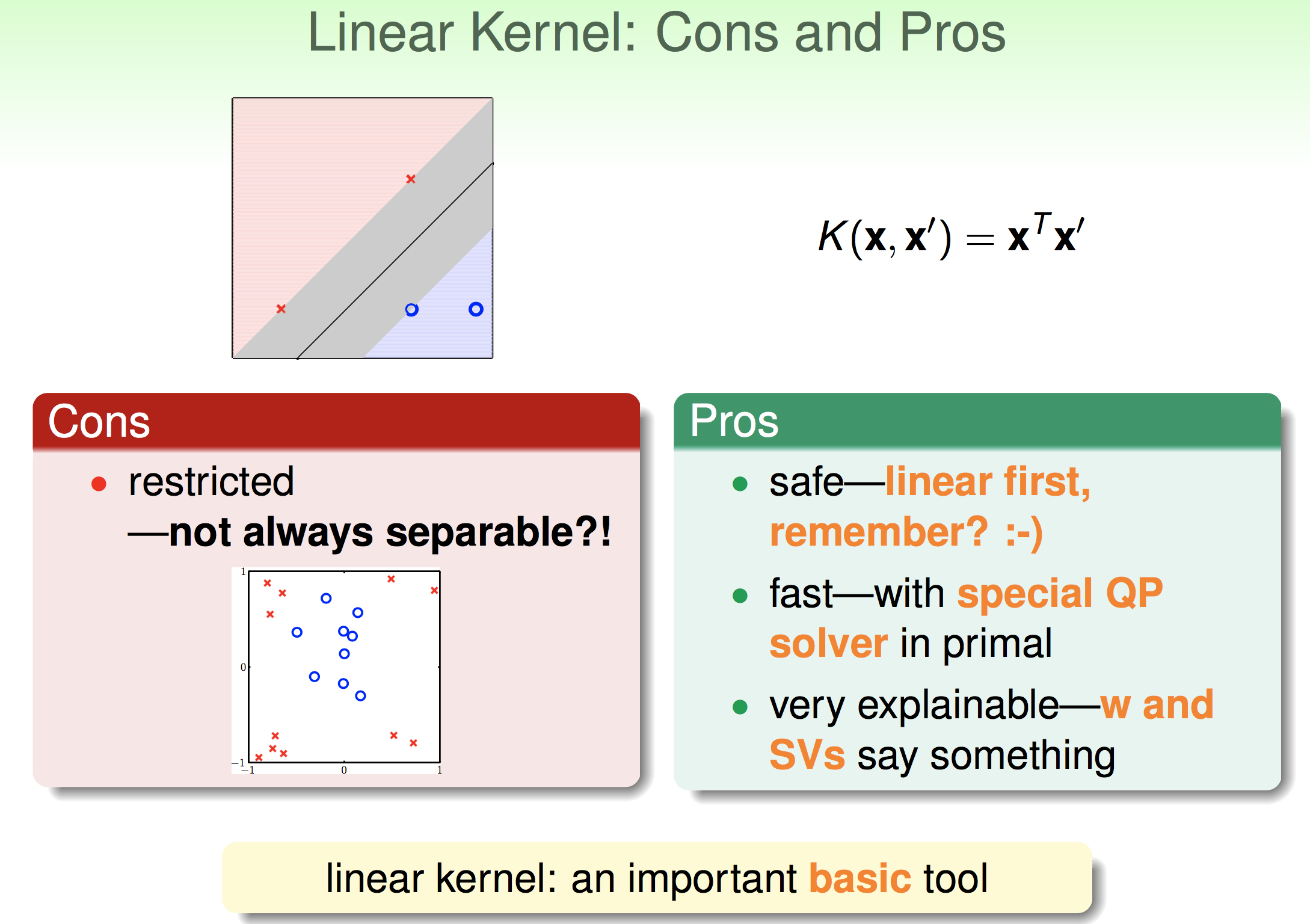
　　如果要用SVM来做非线性的分类，我们采用的方法是将原来的特征空间映射到另一个更高维的空间，在这个更高维的空间做线性的SVM。即：

在这里我们计算这个向量内积有两种方法：一种是对Φ(x)给出明确的定义，分别算出两个高维向量，再做内积；另一种就是利用核函数，直接算出高维的内积。我们以一个例子来看这两种方法，定义一个二次转化：

我们可以直接计算出内积：

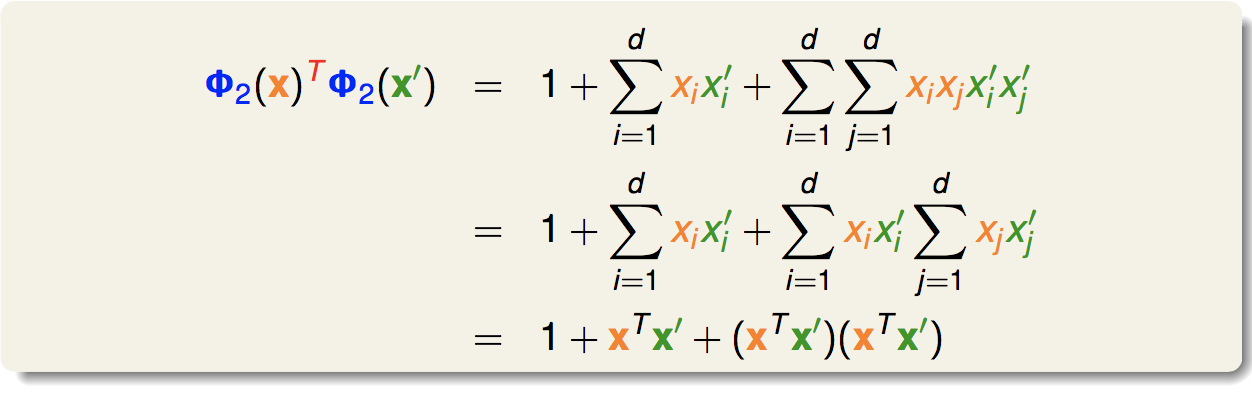
可以看出，最后的结果能够用x和x一撇表示出来，这就是一个核函数：

在这里，我们是给出了一个Φ(x)来推出它的核函数。但事实上，我们可以直接给一个核函数（只要我们能证明它是一个核函数），而不用知道它对应的Φ(x)是什么。这样做的一个好处就是我们不用求出高维向量在做内积，可以通过形式简单的核函数直接计算内积，计算复杂度降低了，到后面我们用核函数甚至可以引入无限维的转换。

我们的b值就是：

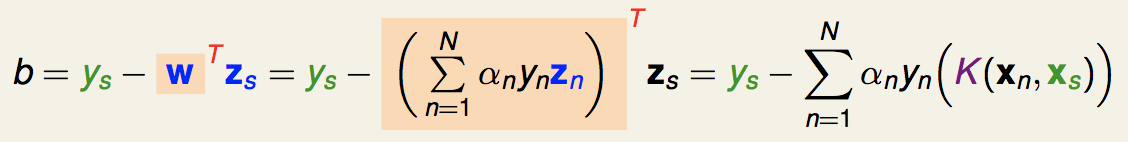
最终得到的分离超平面就是：

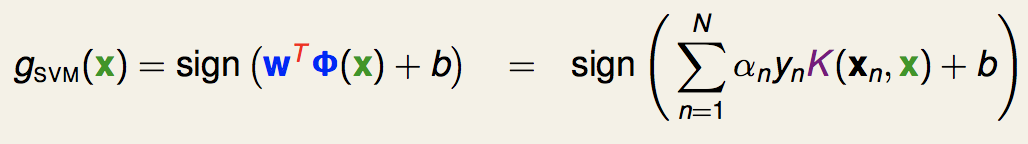
可以看出，不管是求解的优化问题还是最后的模型，我们都可以用核函数来表示。（这里我们不用知道w是什么）

因此，通过核函数的引入，我们相当于隐式的在高维空间进行线性SVM，而不用知道低维到高维的具体映射是什么。

关于使用核函数后的时间复杂度的优化，如下：

2 .多项式核函数

首先对一个常用的核函数——二次多项式核函数做导出：

对于不同的二次核，我们产生的决策边界是不同的：

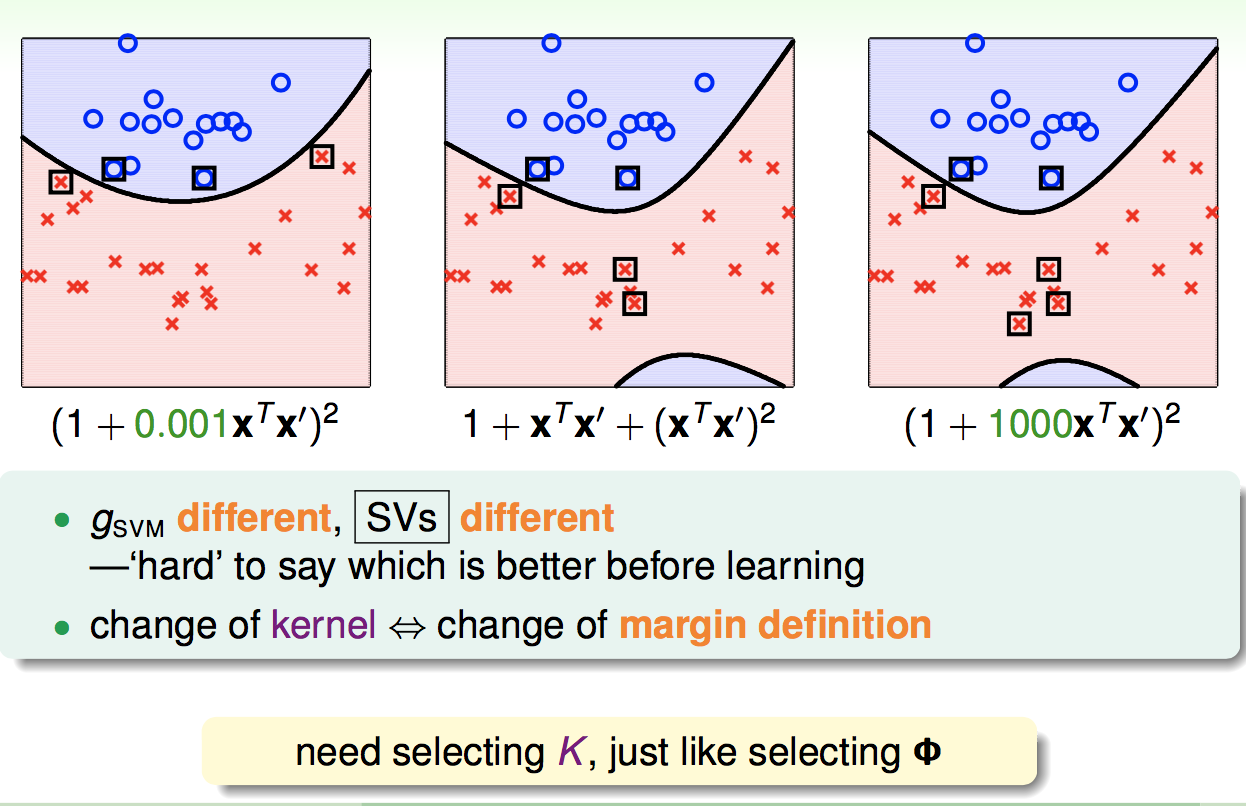
之后我们可以推广出通用的多项式核函数：

3. 高斯核函数

我们可以证明高斯核函数是一个核函数，并且它对应一个到无限维的映射：

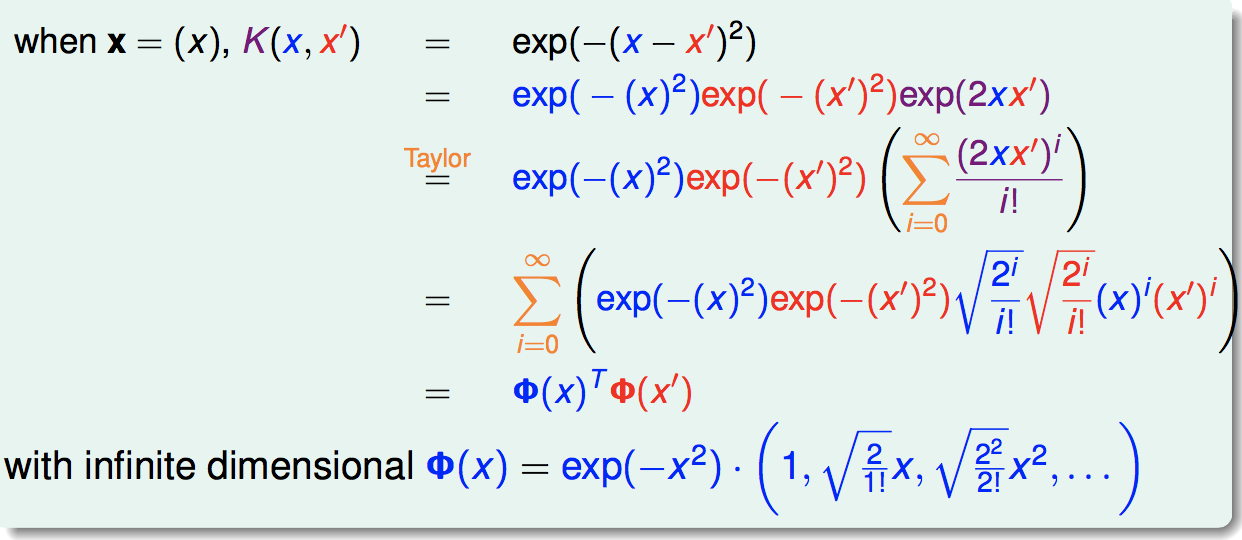
更通用的高斯核函数为：

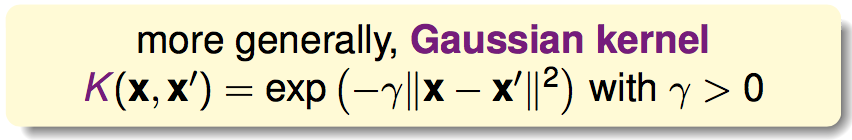
高斯核SVM的分离超平面就是：

可以看出，模型是一堆中心在支撑向量上的高斯函数的线性组合，因此高斯核SVM也被称为RBF。

总结一下，SVM可以做的事情：

首先是有分离超平面，然后引入了的高维度转换（使得我们可以做非线性分类），然后使用了核技巧（使得我们降低了复杂度并且可以引入无限维的转换），在这些基础上，SVM有它的large-margin机制来确保我们的模型复杂度比较小（泛化能力）。

最后存储模型的时候，我们不用存储高维度的w，存储的是支持向量以及它们对应的阿尔法值。

接下来我们看看不同的高斯核svm产生的边界：

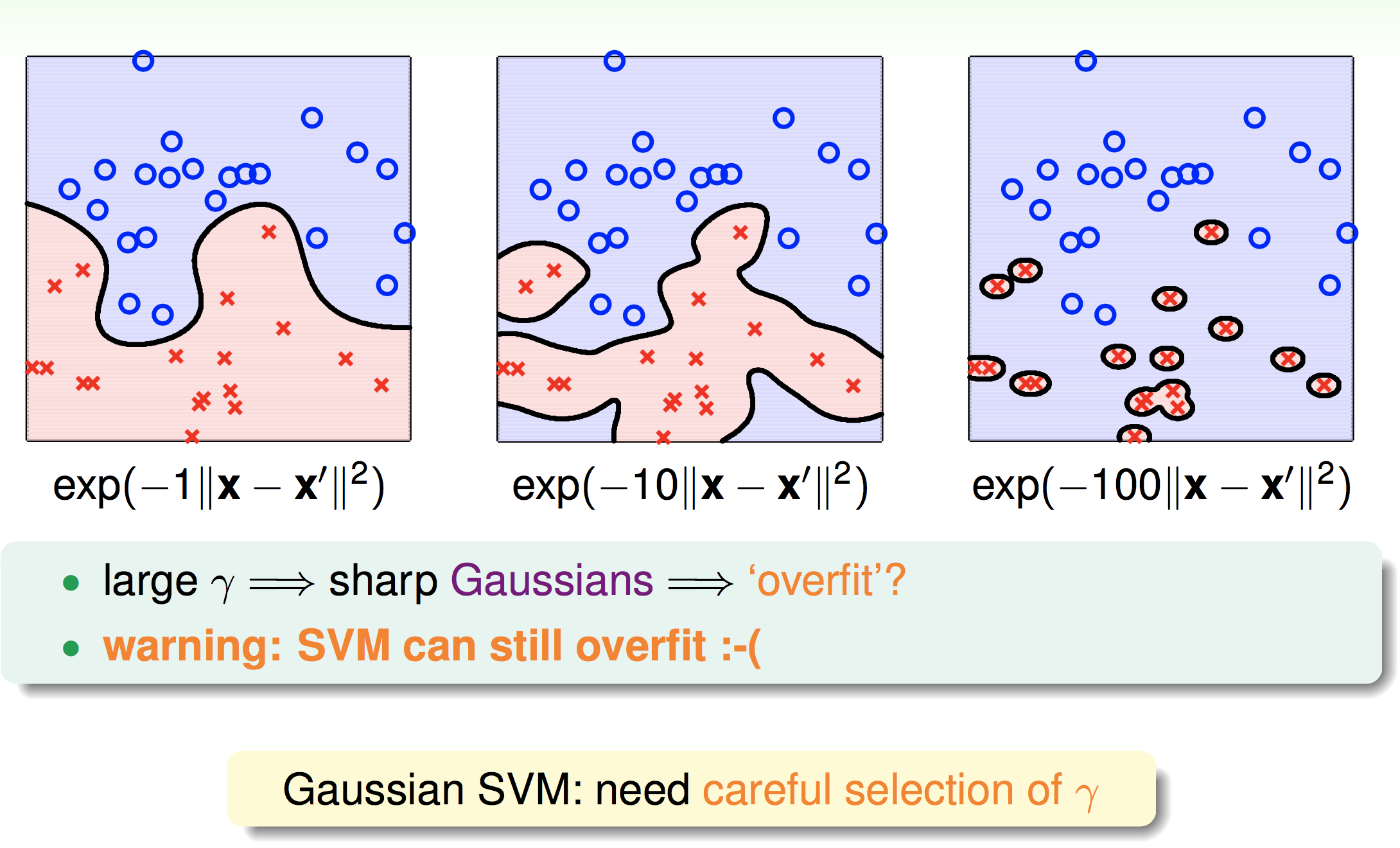
因此，即使SVM有large-margin的保护，但是还是要慎选伽马的值，否则仍然会过拟合。

4.几种核函数的比较