POJ 3436 ACM Computer Factory

题意:

 

为了追求ACM比赛的公平性，所有用作ACM比赛的电脑性能是一样的，而ACM董事会专门有一条生产线来生产这样的电脑，随着比赛规模的越来越大，生产线的生产能力不能满足需要，所以说ACM董事会想要重新建造一条生产线。

        生产线是全自动化的，所以需要机器来组成生产线，给定有多少中种机器，标准ACM用电脑有多少部份，每种机器将什么样的ACM电脑半成品处理成什么样的电脑半成品(对于输入的电脑半成品，每部分有0，1，2三种状态：代表着 0、这部分必须没有我才能处理，1、这部分必须有我才能处理，2、这部分有没有我都能处理。对于输出的电脑半成品有0，1两种状态：代表着0，处理完后的电脑半成品里没有这部分，1、处理完的电脑半成品有这部分)，每一个机器每小时可以处理Q个半成品（输入数据中的Qi）。

        求组装好的成产线的最大工作效率（每小时最多生成多少成品，成品的定义就是所有部分的状态都是“1”）

 

第一行输入两个数：一个P代表有P个零件， 一个 N代表有N台机器。

接下来N行，每行第一个数字有Qi，代表 第i个零件每小时能加工的半成品零件个数。然后是2*P个数字，前P个数字是加工前半成品需要满足的条件，后P个数表示加工后的半成品的数量。

===========================================================================

思路： 

首先要把点分割开，把点分开成两部分的意义在于，不能让最大流量超过本身的生产量。

 

==============================================================================================================

由第一副图可知，假如我们不拆分点，那么到达F的流量就是30， 主要原因是流经C点的时候，我们的总流量是超过C可以处理的最大流量的，但是每一个自流量是小于C能处理的最大流量的，但是我们又无法加以限制。因此会出现这样的问题。第二幅图我们就将拆点了，将C到C' 之间的流量加以限制。这样就不会超过最大流量。

==============================================================================================

最后我们这道题目处理出来的模型是这样的（和二分匹配可）：

============================================================================================================

最后一个点就是如何输出路径。

路径的输出是要保存两个图，保存原图，和做完Dinic之后的残余网路图。

然后用原图减去残余网路图如果边权值大于0，说明这个边上曾经有过流量。

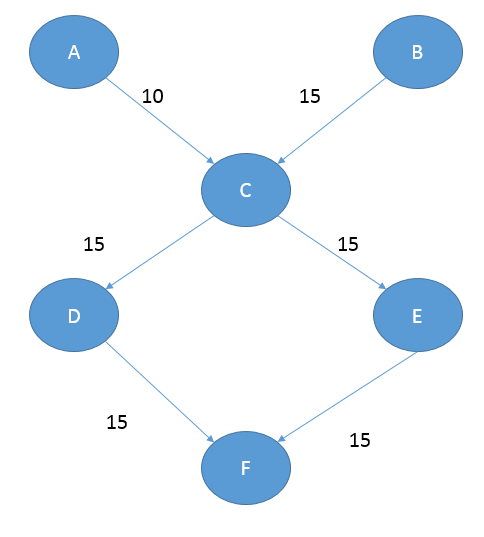
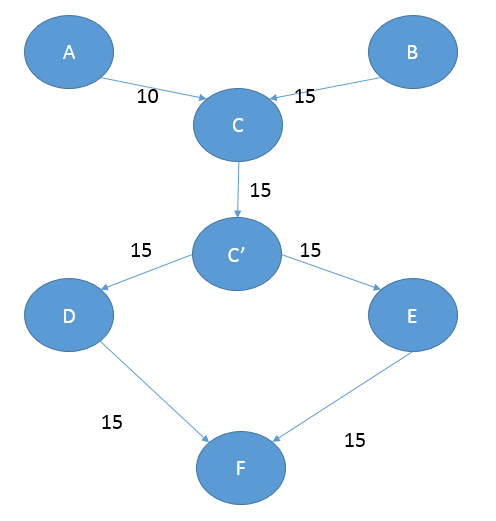
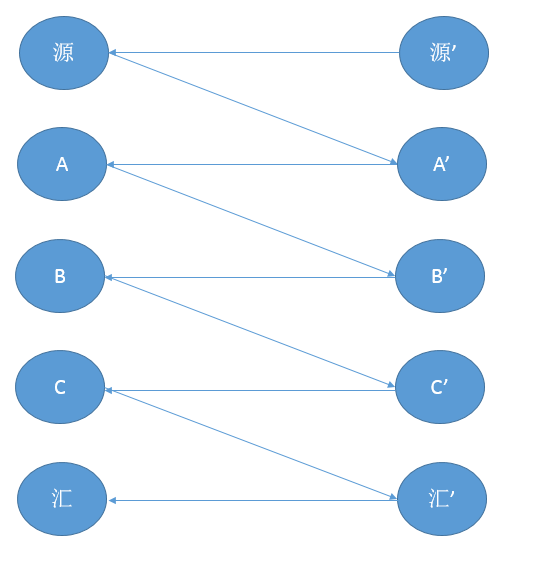
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
using namespace std;
typedef long long LL;
const int INF = 1e9+;
const int maxn = ;
const int MOD = 1e9+;

int G[maxn][maxn], Layer[maxn], G2[maxn][maxn];
struct node
{
    int in[], out[];///第i台机器的输入输出规格
    int flow;///第i台机器能放出的最大流量
} P[maxn];
int n, m;///n台机器，每台机器需要m个零件

bool OK(int a,int b)
{
    for(int i=; i<=m; i++)
    {
        if( !(P[a].out[i] == P[b].in[i] || P[b].in[i] == ) )
            return false;
    }
    return true;
}

bool BFS(int Star,int End)
{
    memset(Layer, , sizeof(Layer));
    Layer[Star] = ;
    queue<int> Q;
    Q.push(Star);

    while( Q.size() )
    {
        int s = Q.front();
        Q.pop();

        if(s == End) return true;

        for(int i=; i<= End; i++)
        {
            if(G[s][i] && !Layer[i])
            {
                Layer[i] = Layer[s] + ;
                Q.push(i);
            }
        }
    }
    return false;
}
int DFS(int s,int End, int MaxFlow)
{
    if(s == End) return MaxFlow;

    int sFlow = ;///从s出发到达汇点的最大流量

    for(int i=; i<=End; i++)
    {
        int flow = G[s][i];

        if( G[s][i]== || Layer[s]+ != Layer[i] ) continue;

        flow = min(MaxFlow-sFlow, flow);
        flow = DFS(i, End, flow);
        G[s][i] -= flow;
        G[i][s] += flow;
        sFlow += flow;
        if(sFlow == MaxFlow)
            break ;
    }
    if(sFlow == )
        Layer[s] = ;
    return sFlow;
}

int Dinic(int Star,int End)
{
    int ans = ;
    while( BFS(Star, End) )
    {
        ans += DFS(Star, End, INF);
    }
    return ans;
}

int main()
{

    while(scanf("%d %d", &m, &n) != EOF)
    {
        memset(G, , sizeof(G));
        memset(P, , sizeof(P));
        for(int i=; i<=n; i++)
        {
            scanf("%d", &P[i].flow);
            for(int j=; j<=m; j++)
                scanf("%d", &P[i].in[j]);

            for(int j=; j<=m; j++)
                scanf("%d", &P[i].out[j]);
        }
        for(int i=; i<=m; i++)
        {
            P[].in[i] = P[].out[i] = ;
            P[n+].in[i] = P[n+].out[i] = ;
        }
        P[].flow = P[n+].flow = INF;
        n ++;

        for(int i=; i<=n; i++)
        for(int j=; j<=n; j++)
        {
            if(i == j)
                G[j+n][i] = P[i].flow;
            else if( OK(i, j) )
                G[i][j+n] = P[i].flow;
        }
        memcpy(G2, G,  sizeof(G));
        int MaxFlow = Dinic(, n*);
        int num = , a[maxn], b[maxn], c[maxn];

        for(int i=; i<n; i++)
        for(int j=; j<n; j++)
        {
            if(i == j)continue;

            if(G2[i][j+n] > G[i][j+n])
            {
                a[num] = i, b[num] = j;
                c[num++] = G2[i][j+n] - G[i][j+n];
            }
        }

        printf("%d %d\n", MaxFlow, num);

        for(int i=; i<num; i++)
            printf("%d %d %d\n", a[i], b[i], c[i]);

    }
    return ;
}
/*
3 5
5   0 0 0  0 1 0
100 0 1 0  1 0 1
3   0 1 0  1 1 0
1   1 0 1  1 1 0
300 1 1 2  1 1 1
*/