bzoj2067: [Poi2004]SZN

Description

String-Toys joint-stock 公司需要你帮他们解决一个问题. 他们想制造一个没有环的连通图模型. 每个图都是由一些顶点和特定数量的边构成. 每个顶点都可以连向许多的其他顶点.一个图是连通且无环的. 图是由许多的线做成的.一条线是一条连接图中两个顶点之间的路径.由于一些技术原因,两条线之间不能有重叠的部分,要保证图中任意一条边都被且仅被一条线所覆盖.由于一些技术原因,做一个这样的图的模型的费用取决于用了多少条线以及最长的那条的长度. (每条边的长度都为1.),给出对应的图,求出最少能用多少条线以及在用最少线的情况下最长的那根线最短可以为多少.

Input

第一行仅包含一个数n – 顶点的总数, 2 <= n <= 10 000. 顶点从1 到 n进行编号. 接下来的n - 1 行描述这些边, 每行两个数a 和 b, 1 <= a, b <= n, a <> b. 表示顶点a和顶点b之间有一条边.

Output

输出两个数,最少用多少条线以及在用最少线的情况下最长线最短可以为多少.

Sample Input

9
7 8
4 5
5 6
1 2
3
2
9 8
2 5
5 8

Sample Output

4 2

HINT

 

考虑从1开始dfs，每次对于子树两个两个合并，多出来的往上合，第一问答案就是1+Σ(deg[x]-1)>>1

第二问答案显然具有可二分性，现在只需要判断答案x合不合法

对于每个点，把它子树所有点向上需要的答案统计出来到list[]中。

如果子树个数是偶数且这个点不是1号点，则额外加一个a[i]=0(因为有可能将一支向上连会更优，例子在后面)

然后对a排序，二分删掉a中的一个元素，从大到小匹配判断是否合法，如果任何方案都不合法，则是不合法的直接退出

如果弄到最后都合法，这个答案就合法，不过要注意判断根的时候如果子树是偶数个不能额外加元素，也不能二分判断，而要直接判断合法性

例子：

19

3 6

11 14

14 19

12 7

8 5

10 4

3 11

7 18

17 2

6 12

3 10

11 1

11 8

9 16

1 9

16 15

15 13

4 17

图：

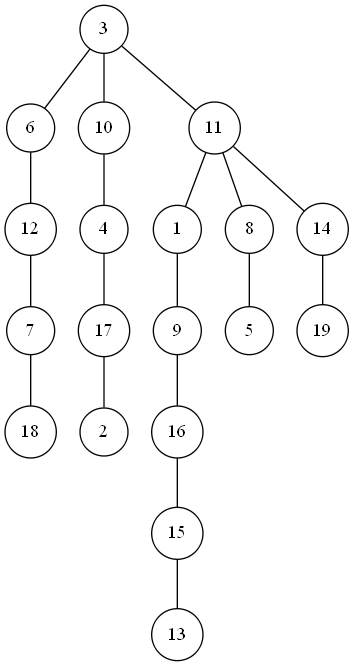
code：

 #include<cstdio>
 #include<iostream>
 #include<cmath>
 #include<cstring>
 #include<algorithm>
 #define maxn 10005
 #define inf 1061109567
 using namespace std;
 char ch;
 int n,a,b,tot,ans,now[maxn],son[maxn<<],pre[maxn<<],deg[maxn],cnt,up[maxn],list[maxn];
 bool ok;
 void read(int &x){
     for (ok=,ch=getchar();!isdigit(ch);ch=getchar()) if (ch=='-') ok=;
     for (x=;isdigit(ch);x=x*+ch-'',ch=getchar());
     if (ok) x=-x;
 }
 void put(int a,int b){pre[++tot]=now[a],now[a]=tot,son[tot]=b,deg[a]++;}
 bool check(int x,int lim){
     for (int i=,j=cnt;i<j;i++,j--){
         if (i==x) i++; if (j==x) j--;
         if (list[i]+list[j]>lim) return false;
     }
     return true;
 }
 bool dfs(int u,int fa,int lim){
     for (int p=now[u],v=son[p];p;p=pre[p],v=son[p])
         if (v!=fa) if (!dfs(v,u,lim)) return false;
     cnt=;
     for (int p=now[u],v=son[p];p;p=pre[p],v=son[p])
         if (v!=fa) list[++cnt]=up[v]+;
     if (!cnt) return true;
     if (u!=&&!(cnt&)) list[++cnt]=;
     sort(list+,list+cnt+);
     if (u==&&!(cnt&)) return check(,lim);
     int l=,r=cnt,m;
     while (l!=r){
         m=(l+r)>>;
         if (check(m,lim)) r=m; else l=m+;
     }
     if (check(l,lim)) up[u]=list[l];
     else up[u]=inf;
     return up[u]<=lim;
 }
 int calc(){
     int l=,r=n-,m;
     while (l<r){
         m=(l+r)>>;
         if (dfs(,,m)) r=m;
         else l=m+;
     }
     return l;
 }
 int main(){
     while (~scanf("%d",&n)){
         tot=;
         memset(now,,sizeof(now));
         memset(deg,,sizeof(deg));
         memset(up,,sizeof(up));
         for (int i=;i<n;i++) read(a),read(b),put(a,b),put(b,a);
         ans=;
         for (int i=;i<=n;i++) ans+=(deg[i]-)>>;
         printf("%d %d\n",ans,calc());
     }
     return ;
 }