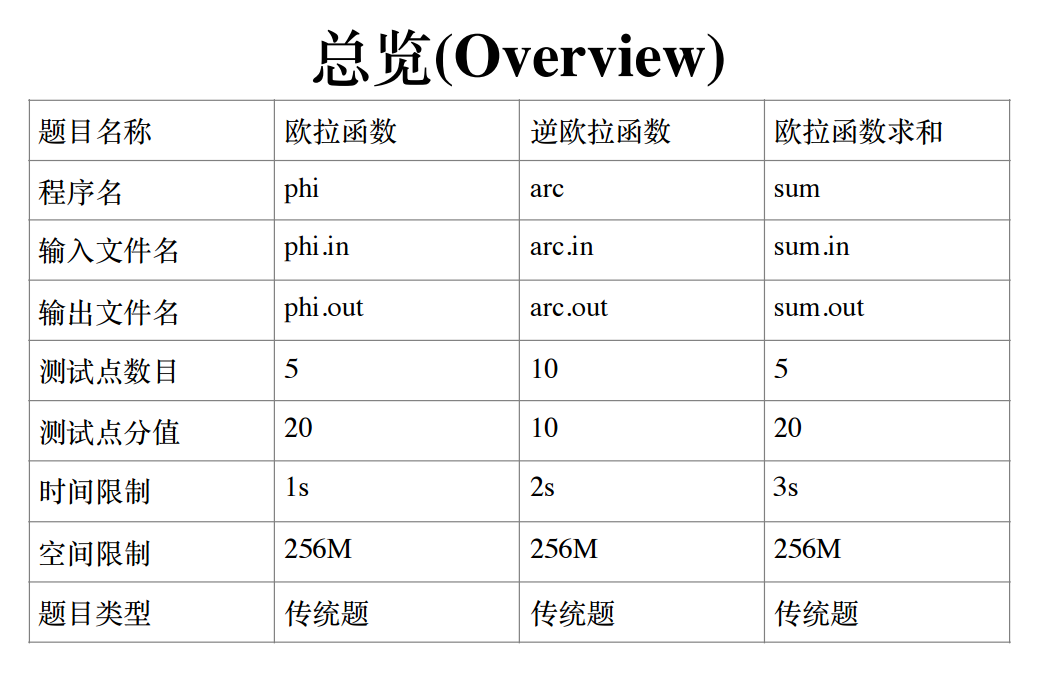
11.2 afternoon

#include<iostream>
#include<cstdio>
#define ll long long
using namespace std;
ll n,ans;
int main()
{
    freopen("phi.in","r",stdin);
    freopen("phi.out","w",stdout);
    cin>>n;ans=n;
    for(ll i=;i*i<=n;i++){
        if(n%i==){
            while(n%i==)n/=i;
            ans=ans/i*(i-);
        }
    }
    if(n>)ans=ans/n*(n-);
    cout<<ans<<endl;
    fclose(stdin);fclose(stdout);
    return ;
}

暴力40不粘了

正解很好的思路

/*
公式变形 F[n]=p1^(a1-1)*(p1-1) + p2^(a2-1)*(p2-1) + ....
Dfs 每个 p a
如果剩下一项 p-1 p是素数 就不用再分解了
可以特判掉 判断比较大的数是不是素数 这里用的 Miller Rabin 或者 Fermat
这不是重点 说不定sqrt暴力判常熟写的小一点也能过 没试过233 

还有一点就是 为什么 x+1>prime[num]的时候才直接放进去
一开始认为的是防止小的多次统计 但是去重之后答案还是不对
似乎还有什么没有想到的 如果有大神想到了为什么 欢迎留言
*/
#include<cstdio>
#include<ctime>
#include<iostream>
#include<cstdlib>
#include<algorithm>
#define ll long long
#define maxn 100010
#define C 10000000
using namespace std;
ll n,k,prime[C/],num,ans[maxn];
bool f[C+];
void Get(){
    int x=min((ll)C,n*);
    for(int i=;i<=x;i++){
        if(f[i]==)prime[++num]=i;
        for(int j=;j<=num;j++){
            if(i*prime[j]>x)break;
            f[i*prime[j]]=;
            if(i%prime[j]==)break;
        }
    }
}
ll mul(ll x,ll y,ll z){
    ll r=;
    while(y){
        if(y&){
            r+=x;r%=z;y--;
        }
        x<<=;x%=z;y>>=;
    }
    return r;
}
ll Qc(ll x,ll y,ll z){
    ll r=;
    while(y){
        if(y&)r=mul(r,x,z);
        y>>=;x=mul(x,x,z);
    }
    return r;
}
/*
bool Is_prime(ll x){
    for(ll i=1;i<=10;i++){
        ll y=rand()%C+1;
        if(y<0)y=-y;
        ll z=Qc(y,x-1,x);
        if(z!=1)return 0;
    }
    return 1;
}*/
bool Is_prime(ll n)
{
    if(n<)return ;
    if(n==)return ;
    if(n%==)return ;
    ll m=n-,j=;
    while(m%==) {
          j++;
          m >>=;
    }
    for(int i=;i<=;i++){
        ll a=rand()%(n-)+;
        ll x=Qc(a,m,n);
        ll y;
        for(int k=;k<=j;k++){
            y=mul(x,x,n);
            if(y==&&x!=&&x!=n-)return ;
            x=y;
        }
        if(x!=)return ;
    }
    return ;
}
void Dfs(ll x,ll y,int z){
    if(x==){
        ans[++ans[]]=y;return;
    }
    if(z<=)return;
    if(x+>prime[num]&&Is_prime(x+))// ?????
        ans[++ans[]]=y*(x+);
    for(int i=z;i>=;i--)
        if(x%(prime[i]-)==){
            ll a=x/(prime[i]-),b=y,c=;
            while(a%c==){
                b*=prime[i];Dfs(a/c,b,i-);c*=prime[i];
            }
        }
}
int main()
{
    freopen("arc.in","r",stdin);
    freopen("arc.out","w",stdout);
    cin>>n>>k;srand(time());
    Get();Dfs(n,,num);
    sort(ans+,ans++ans[]);
    for(int i=;i<=k;i++)
        cout<<ans[i]<<" ";
    return ;
}

暴力筛法60

#include<iostream>
#include<cstdio>
#define ll long long
#define maxn 10000010
using namespace std;
int n;
ll ans,f[maxn];
void X(ll x)
{
    for(int i=;i<=x;i++)f[i]=i;
    for(int i=;i<=x/;i++){
        if(f[i]==i){
            for(int j=i;j<=x;j+=i){
                f[j]=f[j]*(i-)/i;
            }
        }
    }
}
int main()
{
    freopen("sum.in","r",stdin);
    freopen("sum.out","w",stdout);
    cin>>n;
    if(n==){
        cout<<""<<endl;return ;
    }
    X(n);ans=;
    for(int i=;i<=n;i++){
        if(f[i]==i)f[i]--;
        ans+=f[i];
    }
    cout<<ans<<endl;
    fclose(stdin);fclose(stdout);
    return ;
}