Trie和Ternary Search Tree介绍

Trie树

Trie树，又称字典树，单词查找树或者前缀树，是一种用于快速检索的多叉树结构，如英文字母的字典树是一个26叉树，数字的字典树是一个10叉树。

Trie树与二叉搜索树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀（prefix），也就是这个节点对应的字符串，而根节点对应空字符串。一般情况下，不是所有的节点都有对应的值，只有叶子节点和部分内部节点所对应的键才有相关的值。

个节点保存了8个字符串tea，ted，ten，to，A，i，in，inn。

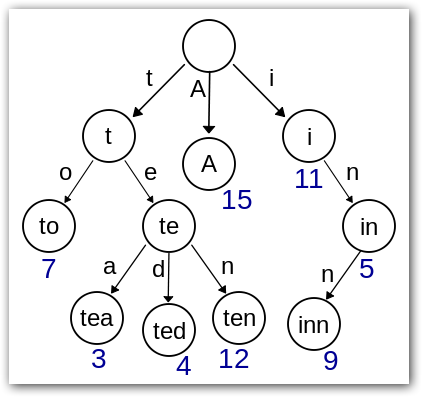
我们注意到Trie树中，字符串tea，ted和ten的相同的前缀（prefix）为"te"，如果我们要存储的字符串大部分都具有相同的前缀（prefix），那么该Trie树结构可以节省大量内存空间，因为Trie树中每个单词都是通过character by character方法进行存储，所以具有相同前缀单词是共享前缀节点的。

当然，如果Trie树中存在大量字符串，并且这些字符串基本上没有公共前缀，那么相应的Trie树将非常消耗内存空间，Trie的缺点是空指针耗费内存空间。

Trie树的基本性质可以归纳为：

）根节点不包含字符，除根节点外的每个节点只包含一个字符。

）从根节点到某一个节点，路径上经过的字符连接起来，为该节点对应的字符串。

）每个节点的所有子节点包含的字符串不相同。

三分搜索树：

个英文字母，每个节点就要保存26个指针，假若我们还要支持国际字符、标点符号、区分大小写，内存用量就会急剧上升，以至于不可行。

由于节点数组中保存的空指针占用了太多内存，我们遇到的困难与此有关，因此可以考虑改用其他数据结构去代替，比如用hash map。然而，管理成千上万个hash map肯定也不是什么好主意，而且它使数据的相对顺序信息丢失，所以我们还是去看看另一种更好解法吧——Ternary Tree。

接下来，我们将介绍三叉搜索树，它结合字典树的时间效率和二叉搜索树的空间效率优点。

和Trie类似，由于三叉搜索树每个节点只有三个叉，所以我们在进行节点插入操作时，只需判断插入的字符与当前节点的关系（少于，等于或大于）插入到相应的节点就OK了。

我们使用之前的例子，把字符串AB，ABBA，ABCD和BCD插入到三叉搜索树中，首先往树中插入了字符串AB，接着我们插入字符串ABCD，由于ABCD与AB有相同的前缀AB，所以C节点都是存储到B的CenterChild中，D存储到C的CenterChild中；当插入ABBA时，由于ABBA与AB有相同的前缀AB，而B字符少于字符C，所以B存储到C的LeftChild中；当插入BCD时，由于字符B大于字符A，所以B存储到C的RightChild中。

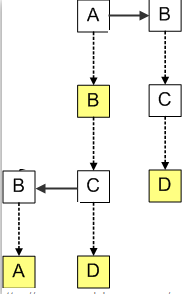
我们注意到插入字符串的顺序会影响三叉搜索树的结构，为了取得最佳性能，字符串应该以随机的顺序插入到三叉树搜索树中，尤其不应该按字母顺序插入，否则对应于单个Trie

节点的子树会退化成链表，极大地增加查找成本。当然我们还可以采用一些方法来实现自平衡的三叉树。

由于树是否平衡取决于单词的读入顺序，如果按排序后的顺序插入，则该方式生成的树是最不平衡的。单词的读入顺序对于创建平衡的三叉搜索树很重要，所以我们通过选择一个排序后数据集合的中间值，并把它作为开始节点，通过不断折半插入中间值，我们就可以创建一棵平衡的三叉树。