poj 2125(最小割)

题目链接：http://poj.org/problem?id=2125

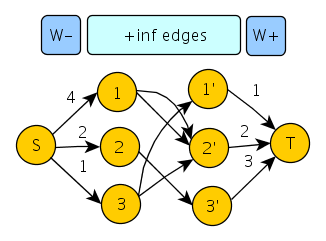
思路：将最小点权覆盖转化为最小割模型，于是拆点建图，将点i拆成i,i+n，其中vs与i相连，边容量为w[i]-,i+n与vt相连，边容量为w[i]+,如果i,j有边相连，则i与j+n连边inf.从而跑最大流求解。对于输出解决放案，我们可以在残余网络中进行dfs,从vs出发，对于那些i<=n没有遍历到的点，说明被取走了，输出‘-’，对于那些i>n遍历到的点,说明之前有j->i的边（j<=n),vs->j不是最小割中的边，i是最小割中的点，输出‘+’。

copy一张图：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<queue>
 using namespace std;
 #define MAXN 222
 #define MAXM 2222222
 #define inf 1<<30

 struct Edge{
     int v,cap,next;
 }edge[MAXM];

 int n,m,NE,vs,vt,NV;
 int head[MAXN];

 void Insert(int u,int v,int cap)
 {
     edge[NE].v=v;
     edge[NE].cap=cap;
     edge[NE].next=head[u];
     head[u]=NE++;

     edge[NE].v=u;
     edge[NE].cap=;
     edge[NE].next=head[v];
     head[v]=NE++;
 }

 int from[MAXN],to[MAXN];
 bool map[MAXN][MAXN];

 void Build()
 {
     NE=;
     memset(head,-,sizeof(head));
     vs=,vt=*n+,NV=*n+;
     for(int i=;i<=n;i++){
         Insert(vs,i,to[i]);
         Insert(i+n,vt,from[i]);
         for(int j=;j<=n;j++){
             if(map[i][j])Insert(i,j+n,inf);
         }
     }
 }

 int level[MAXN],gap[MAXN];
 void bfs(int vt)
 {
     memset(level,-,sizeof(level));
     memset(gap,,sizeof(gap));
     level[vt]=;
     gap[level[vt]]++;
     queue<int>que;
     que.push(vt);
     while(!que.empty()){
         int u=que.front();
         que.pop();
         for(int i=head[u];i!=-;i=edge[i].next){
             int v=edge[i].v;
             if(level[v]<){
                 level[v]=level[u]+;
                 gap[level[v]]++;
                 que.push(v);
             }
         }
     }
 }

 int cur[MAXN],pre[MAXN];

 int SAP(int vs,int vt)
 {
     bfs(vt);
     memset(pre,-,sizeof(pre));
     memcpy(cur,head,sizeof(head));
     int maxflow=,aug=inf;
     int u=pre[vs]=vs;
     gap[]=NV;
     while(level[vs]<NV){
         bool flag=false;
         for(int &i=cur[u];i!=-;i=edge[i].next){
             int v=edge[i].v;
             if(edge[i].cap>&&level[u]==level[v]+){
                 flag=true;
                 pre[v]=u;
                 u=v;
                 aug=min(aug,edge[i].cap);
                 if(v==vt){
                     maxflow+=aug;
                     for(u=pre[v];v!=vs;v=u,u=pre[u]){
                         edge[cur[u]].cap-=aug;
                         edge[cur[u]^].cap+=aug;
                     }
                     aug=inf;
                 }
                 break;
             }
         }
         if(flag)continue;
         int minlevel=NV;
         for(int i=head[u];i!=-;i=edge[i].next){
             int v=edge[i].v;
             if(edge[i].cap>&&level[v]<minlevel){
                 minlevel=level[v];
                 cur[u]=i;
             }
         }
         if(--gap[level[u]]==)break;
         level[u]=minlevel+;
         gap[level[u]]++;
         u=pre[u];
     }
     return maxflow;
 }

 bool mark[MAXN];
 void dfs(int u)
 {
     mark[u]=true;
     for(int i=head[u];i!=-;i=edge[i].next){
         int v=edge[i].v;
         if(!mark[v]&&edge[i].cap>)dfs(v);
     }
 }

 int main()
 {
 //   freopen("1.txt","r",stdin);
     int u,v,cnt;
     while(~scanf("%d%d",&n,&m)){
         for(int i=;i<=n;i++)scanf("%d",&from[i]);
         for(int i=;i<=n;i++)scanf("%d",&to[i]);
         memset(map,false,sizeof(map));
         while(m--){
             scanf("%d%d",&u,&v);
             map[u][v]=true;
         }
         Build();
         printf("%d\n",SAP(vs,vt));
         memset(mark,false,sizeof(mark));
         dfs(vs);
         cnt=;
         for(int i=;i<=*n;i++){
             if(!mark[i]&&i<=n)cnt++;
             else if(mark[i]&&i>n)cnt++;
         }
         printf("%d\n",cnt);
         for(int i=;i<=*n;i++){
             if(!mark[i]&&i<=n)printf("%d -\n",i);
             else if(mark[i]&&i>n)printf("%d +\n",i-n);
         }
     }
     return ;
 }