几何+暴力【p1959】 遗址[NOI导刊2009普及(6)]

题目描述--> P1959 遗址_NOI导刊2009普及（6）

普通方法分析：

因为题目要求是找最大正方形(如果是长方形更麻烦.

讲真,题目不难,耗时间!

根据题目要求,我们要找的是正方形.

我们可以根据已知两点去判断其他两点是否存在

然后就到了画图课讲解法的时候.

下面所有的dely代表纵坐标差值,delx代表横坐标差值.

(记得在输入的时候,标记圆柱坐标.

当我们枚举的两个点所在直线平行于x轴或y轴的时候↓.

直线两侧均可能有正方形

(即横坐标差值为0或纵坐标差值为0的时候.)

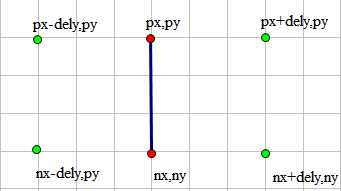
纵坐标相同的话,加减横坐标差值即可.

这时只需要判断其他位置点是否存在即可.

我们的难点在于如何判断两个点是倾斜的情况.

容易发现一个将一个倾斜正方形围起来之后,四个三角形是相等的. 像这样↓

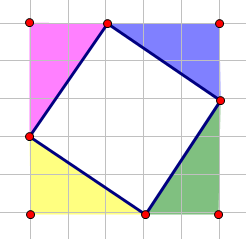
很明显全等吧!证明过程略

然后我们需要考虑的是两个点所在直线斜率是正还是负的问题

(亲测只考虑一种情况,不能AC此题.)

求斜率的公式： k=Δy/Δx

分母不能为0!

然后我们又开始画图 emmm

斜率为负有两种情况.我们可以画图如下↓

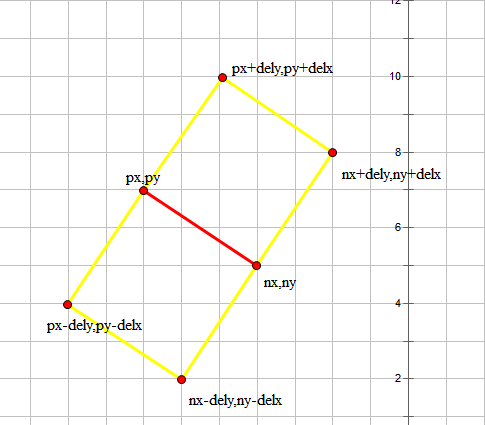
斜率为正.同样有两种情况如下↓

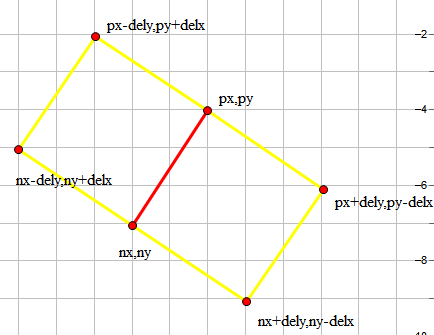
按照图片去写代码即可.

--------------------代码---------------------

#include<bits/stdc++.h>
#define IL inline
#define RI register int
IL void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(s>'9' or s<'0'){if(s=='-')f=-1;s=getchar();}
	while(s<='9' and s>='0'){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,x[30008],y[30008];
bool res[6008][6008];
int ans;
IL int dis(int a,int b){return abs(a-b);}
IL bool ok(int x,int y)
{
	if(x<0 || y<0 || x>5000 || y>5000 || !res[x][y])return false;
	return true;
}
IL void search(int px,int py,int nx,int ny)
{
	int delx=dis(px,nx),dely=dis(py,ny);
	if(delx==0)
	{
		if(ok(px+dely,py) && ok(nx+dely,ny))
			ans=std::max(ans,dely*dely);
		else if(ok(px-dely,py) && ok(nx-dely,ny))
			ans=std::max(ans,dely*dely);
	}
	else if(dely==0)
	{
		if(ok(px,py+delx) && ok(nx,ny+delx))
			 ans=std::max(ans,delx*delx);
		else if(ok(px,py-delx) && ok(nx,ny-delx))
			ans=std::max(ans,delx*delx);
	}
	else if(((ny-py)/(nx-px))<0 && nx-px!=0)
	{
		if(ok(px+dely,py-delx) && ok(nx-dely,ny-delx))
			ans=std::max(delx*delx+dely*dely,ans);
		else if(ok(px+dely,py+delx) && ok(nx+dely,ny+delx))
			ans=std::max(delx*delx+dely*dely,ans);
	}
	else if(((ny-py)/(nx-px))>0 && nx-px!=0)
	{
		if(ok(px+dely,py-delx) && ok(nx+dely,ny-delx))
			ans=std::max(delx*delx+dely*dely,ans);
		else if(ok(px-dely,py+delx) && ok(nx-dely,ny+delx))
			ans=std::max(delx*delx+dely*dely,ans);
	}
}
int main(void)
{
	in(n);
	for(RI i=1;i<=n;i++)
		in(x[i]),in(y[i]),res[x[i]][y[i]]=true;
	for(RI i=1;i<=n;i++)
		for(RI j=1;j<=n;j++)
			if(i!=j)search(x[i],y[i],x[j],y[j]);
	printf("%d",ans);
}

如果RE的话记得判边界,还要判断是否有标记.

可能会有些麻烦,但个人感觉较好理解.

更简单的方法

通过我们的画图.(如果你不知道请向上看图 qwq

我们很容易发现

新点的横坐标,只与dely有关.

新点的纵坐标,只与delx有关.

无论直线如何摆放都是如此.

且对应坐标为一个加一个减.

因此我们可以精简代码成下面这样：

--------------------代码--------------------

#include<bits/stdc++.h>
#define IL inline
#define RI register int
IL void in(int &x)
{
	int f=1;x=0;char s=getchar();
	while(s>'9' or s<'0'){if(s=='-')f=-1;s=getchar();}
	while(s<='9' and s>='0'){x=x*10+s-'0';s=getchar();}
	x*=f;
}
int n,x[30008],y[30008];
bool res[6008][6008];
int ans;
IL int dis(int a,int b){return abs(a-b);}
IL bool ok(int x,int y)
{
	if(x<0 || y<0 || x>5000 || y>5000 || !res[x][y])return false;
	return true;
}
IL void search(int px,int py,int nx,int ny)
{
	int delx=dis(px,nx),dely=dis(py,ny);
	if(ok(px+dely,py-delx) &&ok(nx+dely,ny-delx))
		ans=std::max(ans,delx*delx+dely*dely);
	else if(ok(px-dely,py+delx) && ok(nx-dely,ny+delx))
		ans=std::max(ans,delx*delx+dely*dely);
     //感觉少考虑了斜率为负的那一种情况,但的确是可以AC的.
     /*
     我们也可以加上判断斜率为负的情况.
    else if(ok(px+dely,py+delx) && ok(nx+dely,ny+delx))
		ans=std::max(ans,delx*delx+dely*dely);
	else if(ok(px-dely,py-delx) && ok(nx-dely,ny-delx))
		ans=std::max(ans,delx*delx+dely*dely);
     难道数据水?
     */
}
int main(void)
{
	in(n);
	for(RI i=1;i<=n;i++)
		in(x[i]),in(y[i]),res[x[i]][y[i]]=true;
	for(RI i=1;i<=n;i++)
		for(RI j=1;j<=n;j++)
			if(i!=j)search(x[i],y[i],x[j],y[j]);
	printf("%d",ans);
}

里面的delx*delx+dely*dely 是勾股定理的内容,就不用我多说了吧.

(逃