【例题收藏】◇例题·6◇ 电压机制（voltage）

◆例题·6◆ 电压机制

周六日常模拟赛……已经不知道该说什么了（感觉做不出来的都是好题）

---

▷ 题目

（终于不用自己翻译英文题了╮(╯-╰)╭）

【问题描述】

科学家在“无限神机”（Infinity Machine）找到一个奇怪的机制，这个机制有N个元件，有M条电线连接这些元件，所有元件都是连通的。两个元件之间可能有多条电线连接。

科学家对这些元件可以任意地设置为“高电压”和“低电压”两种模式，如果一条电线的一端为高电压，另一端为低电压，这条电线就会产生电流。

为了安全的研究“无限神机”，科学家需要找到一条电线，将它的两端设为相同的电压，并且除选择的这条电线外，其它所有电线都有电流（否则就没有研究的价值了）。

有多少条电线满足这样的条件？

【输入格式】

从文件 voltage.in 中读入数据。

输入的第一行包含两个正整数 n, m ,表示元件数和电线数。

接下来 m 行，每行两个整数 u, v，表示元件 u 和元件 v 有一条电线连接

【输出格式】

输出到文件 voltage.out 中。

输出一个整数，表示有多少条电线满足条件。

（鬼畜的题目背景就不copy上来了U•ェ•*U）

---

▷ 解析

首先很容易想到，节点的高/低电压就相当于0/1染色，除了题目所提到的“被选择的电线”，其他的边的两个端点的颜色应该不同。听起来是不是特别像二分图？所以可以套用一下判断二分图的DFS……检查是否染色成功。

接下来考虑一下图上的一些性质——环！

① 如果没有环

那么就非常简单了，由于图是全联通的，所以此时图就是一棵树。那么每一条边都可以作为“被选中的边”。原因是：

选择一条边就相当于把它删去，同时将它的两端点染成相同的颜色。但是由于图是一棵树，删除任意一条边都会将树分成两个连通块，两个连通块分别形成一个新的树。既然是树，从一个点开始，就一定可以将整棵树都染上色。

那么上述情况，答案就是边的数量。

② 如果有偶环

很容易想到不能选择在偶环上的边，否则染色就会失败。

比如下面这个例子：

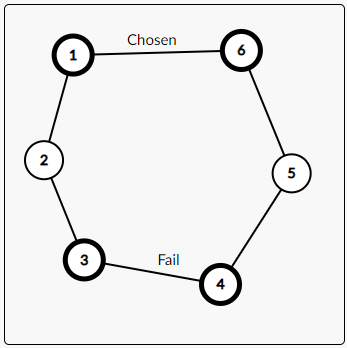
③ 如果有奇环

可以想到选择的边一定要在奇环中，否则会出现下面这种情况：{1,2,3,4,5}构成一个奇环，但是选择了1->6的边，也就相当于从1开始对奇环染色……很明显是无法完成的。

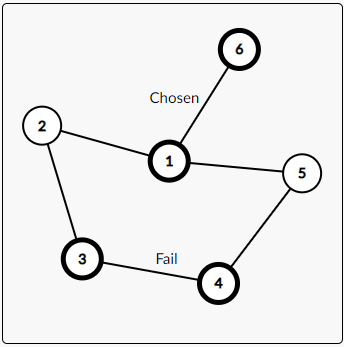
推广一下，对于每一个奇环，只要它没有一条边被选中，它就一定会从它的某一个点开始染色，而这样染色的结果就只有失败。所以所有奇环都必须包含有被选择的边，换句话说，如果我们计算出所有奇环的边集——我们能选择的边就只能是所有奇环的边集的交集！

综上所述，除了情况①，我们要选择的边E要满足以下性质：

1. 设第i个偶环的边集为 A[i] ，则对于每一个i， E ∉ A[i]

2. 设第i个奇环的边集为 B[i] ，则对于每一个i， E ∈B[i]

接下来就是进行一个DFS。由于下面要用到 DFS 树的一些知识，初学者可以先学一下 DFS树（不然可能会自闭(。・∀・)ノ）。

说明一下变量：

1. 整个图的奇环的个数为 odd。

2. 对于一条边存储一个 tot 值表示该边在多少个奇环内，则判断该边是否满足“包含在任何一个奇环内”时，只需要判断它的 tot 是否等于 odd 就可以了。

3. cnt[u] 表示 u 到 u的父亲（在DFS树里） 这一条边包含在多少个奇环里（差分数组）。

从1节点开始DFS，同时进行二分图染色。假设当时在节点u，准备扩展到与u相连的节点v —— 如果v没有染色，就将v染色，继续从v扩展；如果v已经染过色，那么 u->v 是一条返祖边，众所周知，u->v 的返祖边与 u->v 在DFS树上的路径会围成一个环。对于围成环的情况，判断当 u的颜色 和 v的颜色 相同时，就围成了一个奇环，否则围成了一个偶环。如果围成了一个奇环，则将环内的所有边的 tot 都+1；如果围成偶环，则将环内的所有边的 tot 都-1，这样的话 tot 就不可能达到 odd，也就不可能被选择了。

即使上述算法已经比较优秀了，但是仍然会爆炸，因为枚举环上的边时间复杂度太大了！

所以我们需要用到差分，差分数组最显著的性质就是 前缀和 等于原数组。当找到环时，如果是奇环，则 cnt[u]++,cnt[v]--，同时将 u->v 这条返祖边的 tot +1；如果是偶环，则 cnt[u]--,cnt[v]++，同时将 u->v 这条返祖边的 tot -1。除了在找到环时更改 cnt，在回溯时，父亲和儿子之间也存在 cnt 的转换——假设 点u,v 在DFS树中 u 是 v 的父亲，则 cnt[u]+=cnt[v] ，且 u->v 这一条树边的 tot 也 +=cnt[v]。

当整个 DFS 结束后，枚举所有边，判断它的 tot 是否等于 odd，如果是，则 ans++。

（我猜可能有一些 reader 已经自闭了，还是看看代码吧）

---

▷ 源代码

/*Lucky_Glass*/
#include<bits/stdc++.h>
using namespace std;
const int N=100000,M=200000;
struct EDGE{
	int u,v;
}edg[M+5];
struct LINK{
	int v,id;
};
vector< LINK > lnk[N+5];
int n,m;
bool vis[M+5];
int col[N+5],cnt[N+5],tot[M+5],odd;
void DFS(int u){
	for(int i=0;i<lnk[u].size();i++) //枚举相邻的点
		if(!vis[lnk[u][i].id]){ //这条边没有被访问过（防止走重）
			vis[lnk[u][i].id]=true;
			int v=lnk[u][i].v;
			if(col[v]!=-1){ //经过返祖边
				if(col[v]==col[u]){
					odd++; //奇环数量+1
					cnt[u]++;cnt[v]--; //差分数组 u->v 的路径+1
					tot[lnk[u][i].id]++; //返祖边+1
				}
				else{
					cnt[v]++;cnt[u]--; //u->v路径-1，相当于取消选择 u->v 路径上任何一条边的可能性
					tot[lnk[u][i].id]--; //取消选择返祖边的可能性
				}
			}
			else{
				col[v]=!col[u]; //染反色
				DFS(v);
				tot[lnk[u][i].id]+=cnt[v]; //父亲儿子之间的边统计
				cnt[u]+=cnt[v]; //差分前缀和
			}
		}
}
int main(){
	freopen("voltage.in","r",stdin);
	freopen("voltage.out","w",stdout);
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		scanf("%d%d",&edg[i].u,&edg[i].v);
		lnk[edg[i].u].push_back((LINK){edg[i].v,i}); //双向连边
		lnk[edg[i].v].push_back((LINK){edg[i].u,i});
	}
	memset(col,-1,sizeof col); //初始化所有颜色为-1
	col[1]=0; //从节点1开始，先将它染成0
	DFS(1);
	int ans=0;
	for(int i=1;i<=m;i++)
		ans+=int(tot[i]==odd);
	printf("%d\n",ans);
	return 0;
}

　　

---

The End

Thanks for reading!

- Lucky_Glass

（Tab：如果我有没讲清楚的地方可以直接在邮箱lucky_glass@foxmail.com email我，在周末我会尽量解答并完善博客~）