剑指offer js算法练习(1-10)

1.二维数组中的查找
       在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

时间限制：1秒 空间限制：32768K

分析：由于每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序，所以右上角的数字就是该行的最大值，该列的最小值。则可以通过把目标数与右上角的数字比较来判断其位置，如果目标数比该数字小，由该数字为该列的最小值可得这一列都不会有目标数，我们就可以将该列删除，并得到新的二维数组，再次比较目标数与右上角的数字的大小关系。如果目标数比该数字大，由该数字为该行的最大值可得这一行都不会有目标数，我们就可以将该行删除，并得到新的二维数组，再次比较目标数与右上角的数字的大小关系。如果目标数与右上角的数字相等，则返回true，找到了该目标数。如果当行数和列数都被删完了还没找到，则该二维数组中就没有该目标数。

function Find(target, array)
{
    if(array==undefined||array.length<0||array[0].length<0){
        return false;
    }
    let rows=array.length;
    let columns=array[0].length;
    let row=0;
    let column=columns-1;
    while(row<rows&&column>=0){
        if(array[row][column]==target){
            return true;
        }
        if(array[row][column]>target){
            column--;
        }else{
            row++;
        }
    }
    return false;
}

2.替换空格
        请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

时间限制：1秒 空间限制：32768K

分析：这里用replace+正则表达式即可替换。

function replaceSpace(str)
{
    return str.replace(/ /g,'%20')
}

3.从头到尾打印链表
       输入一个链表，按链表值从尾到头的顺序返回一个ArrayList。链表节点如下：

function ListNode(x){
    this.val = x;
    this.next = null;
}

时间限制：1秒 空间限制：32768K

分析：首先我们应该判断链表是否存在，如果链表存在的话，就用一个循环来判断节点是否存在，依次将节点中的值放入栈（题目要求从尾到头的顺序）即可。

function printListFromTailToHead(head)
{
    if(head==undefined)
    {
        return 0;
    }else
    {
        var arr=new Array();
        var curr=head;
        while(curr)
        {
            arr.push(curr.val);
            curr=curr.next;
        }
        return arr.reverse();
    }
}

4.重建二叉树
       输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。树节点如下：

function TreeNode(x) {
    this.val = x;
    this.left = null;
    this.right = null;
} 

时间限制：1秒 空间限制：32768K

分析：首先我们要知道前序遍历的顺序是根左右，中序遍历的顺序是左根右。前遍历的第一个数总是根，所以我们就可以在前序遍历中先找到根，再在中序遍历中分别找到左子树和右子树，然后再分别在左子树和右子树中按照相同的方法去找它们的根节点，左右子树，直到在某个子树中的前序和后序遍历的长度都为0。由此我们可以写出如下的递归代码：

function reConstructBinaryTree(pre, vin)
{
    if(pre.length==0&&vin.length==0)
    {
        return null;
    }
    var index=vin.indexOf(pre[0]);
    var left=vin.slice(0,index);
    var right=vin.slice(index+1);
    var root=new TreeNode(pre[0]);
    root.left=reConstructBinaryTree(pre.slice(1,index+1),left);
    root.right=reConstructBinaryTree(pre.slice(index+1),right);
    return root;
}

5.用两个栈实现队列
       用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

时间限制：1秒 空间限制：32768K

分析：首先我们要明白栈的特点是后进先出,队列的特点是先进先出。这里我们可以用栈stack1压入队列，不做特殊处理，就用栈的方法压入。再在另一个用于Pop的方法中，把stack1中数依次弹出并压入栈stack2，这样就满足了最先进入栈stack1在栈stack2的栈顶，由于Pop操作每次只弹出一个值，所以需要弹出stack2的栈顶值，用一个变量存起来，然后再把stack2中数依次弹出并压入栈stack1，以便下次正常压入弹出，最后返回变量即可。

var stack1=new Array();
var stack2=new Array();

function push(node)
{
    stack1.push(node);
}
function pop()
{
    var temp=stack1.pop();
    while(temp){
        stack2.push(temp);
        temp=stack1.pop();
    }
    var result=stack2.pop();
    temp=stack2.pop();
    while(temp){
        stack1.push(temp);
        temp=stack2.pop();
    }
    return result;
}

6.旋转数组的最小数字
        把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

时间限制：3秒 空间限制：32768K

分析：这道题可以用二分法来做，但是会出现超时，所以用js的Math.min.apply(null,arr)方法来求是最高效的。

function minNumberInRotateArray(rotateArray)
{
    if(rotateArray.length==0){
        return 0;
    }
    return Math.min.apply(null,rotateArray);
}

7.斐波那契数列
        大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项（从0开始，第0项为0）。n<=39

时间限制：1秒 空间限制：32768K

分析：斐波那契数列指的是这样一个数列 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368........这个数列从第3项开始，每一项都等于前两项之和。解决斐波那契数列可以使用递归的解法，但是这个却不是最优解，因为递归会产生很多重复的计算。为避免重复计算，我们可以根据f(0)和f(1)算出f(2),再根据f(1)和f(2)算出f(3)......依次类推就可以算出第n项了。

function Fibonacci(n){
    if(n<0||n>39){
        return;
    }
    if(n==0){
        return 0;
    }
    if(n==1){
        return 1;
    }
    var fibNMinusOne=0;
    var fibNMinusTwo=1;
    var fibN=0;
    for(var i=2;i<=n;i++){
        fibN=fibNMinusOne+fibNMinusTwo;
        fibNMinusOne=fibNMinusTwo;
        fibNMinusTwo=fibN;
    }
    return fibN;
}

8.跳台阶
        一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

时间限制：1秒 空间限制：32768K

分析：首先我们考虑最简单的情况。如果只有1级台阶，那显然只有一种跳法。如果有2级台阶，那就有两种跳法：一种是分两次跳，每次跳1级；另一种就是一次跳2级。接着我们再来讨论一般情况。我们把n级台阶时的跳法看成n的函数，记为f(n)。当n>2时，第一次跳的时候就有两种不同的选择：一次第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1);二是第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)。因此，n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。这实际上就是斐波那契数列。

function jumpFloor(number){
    if(number <= 0){
        return 0;
    }
    if(number == 1){
        return 1;
    }
    if(number == 2){
         return 2;
    }
    var jumpNMinusOne=1;
    var jumpNMinusTwo=2;
    var jumpN=0;
    for(var i=3;i<=number;i++){
        jumpN=jumpNMinusOne+jumpNMinusTwo;
        jumpNMinusOne=jumpNMinusTwo;
        jumpNMinusTwo=jumpN;
    }
    return jumpN;
}

9.变态跳台阶
        一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

时间限制：1秒 空间限制：32768K​​​​​​​

分析：首先我们考虑最简单的情况。如果只有1级台阶，那显然只有一种跳法。如果有2级台阶，那就有两种跳法：一种是分两次跳，每次跳1级；另一种就是一次跳2级。如果只有3级台阶，那就有4种跳法：①分三次跳，每次跳1级；②分二次跳，第一次跳2级第二次跳1级；③分二次跳，第一次跳1级第二次跳2级；④分一次跳，直接跳3级。接着我们再来讨论一般情况。我们把n级台阶时的跳法看成n的函数，记为f(n)。当n>1时，第一次跳的时候就有n种不同的选择：第一次只跳1级，此时跳法数目等于后面剩下的n-1级台阶的跳法数目，即为f(n-1);第一次跳2级，此时跳法数目等于后面剩下的n-2级台阶的跳法数目，即为f(n-2)；同理第一次跳n-1级，此时跳法数目等于后面剩下的1级台阶的跳法数目，即为f(1)；第一次跳n级，此时跳法数目等于后面剩下的0级台阶的跳法数目，即为f(0)也就是0次。因此，n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)+...+f(0)。又因f(n-1)=f(n-2)+f(n-3)+...+f(0)。所以f(n)=2*f(n-1)。

function jumpFloorII(number)
{
    if(number <= 0){
        return 0;
    }
    if(number == 1){
        return 1;
    }
    var jumpNMinus=1;
    var jumpN=0;
    for(var i=2;i<=number;i++){
        jumpN=jumpNMinus*2;
        jumpNMinus=jumpN;
    }
    return jumpN;
}

10.矩形覆盖
        我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？​​​​​​​

时间限制：1秒 空间限制：32768K​​​​​​​

分析：

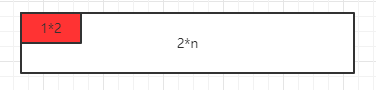
我们讨论一般情况。我们把放的方法的看成n的函数，记为f(n)。当第一个小矩形这样横着放时，剩下的放法即为f(n-2)。

当第一个小矩形这样竖着放时，剩下的放法即为f(n-1)。由此我们可以得到f(n)=f(n-1)+f(n-2)，所以这个问题其实还是斐波那契数列。

function rectCover(number)
{
    if(number==1){
        return 1;
    }
    if(number==2){
        return 2;
    }
    var rectNMinusOne=1;
    var rectNMinusTwo=2;
    var rectN=0;
    for(var i=3;i<=number;i++){
        rectN=rectNMinusOne+rectNMinusTwo;
        rectNMinusOne=rectNMinusTwo;
        rectNMinusTwo=rectN;
    }
    return rectN;
}