JOI2017 春季合宿：Railway Trip

自己的AC做法似乎离正解偏了十万八千里而且复杂了不少……不管怎样还是记录下来吧。

题意：

题目链接：

JOISC2017 F - AtCoder

JOISC2017 F - LOJ

\(N\)个车站排成一行，第\(i\)个车站有一个在\([1,M]\)之间的权值\(l_i\)。有\(M\)种列车，第\(i\)种在所有满足\(l_j \geq i\)的车站\(j\)停靠。如果搭乘一种列车从\(u\)到\(v\)，需要在\(u\)、\(v\)之间的所有停靠站（包含\(u\)和\(v\)），各停车一次，定义这段行程的代价为(\(停车次数-1\))。如果列车\(i\)和\(j\)都在车站\(k\)停靠，允许在车站\(k\)从\(i\)换乘到\(j\)。列车行驶的方向任意。\(Q\)次询问，每次给出起点\(s\)和终点\(t\)，问从\(s\)坐车到\(t\)的最小总代价。

\(1 \leq N,M,Q \leq 10^5\)

思路：

首先试着构出一张无向图，在可以用代价\(1\)转移的点之间连边。

构图方案：

1、标记所有\(l_i=M\)的车站\(i\)，在相邻（中间没有被标记车站）的被标记车站之间连边。

2、新标记所有\(l_i=M-1\)的车站\(i\)（保留先前标记），相邻的被标记车站连边。

3、新标记所有\(l_i=M-2\)的车站\(i\)（保留先前标记），相邻的被标记车站连边。

……

注意到我们标出的这些边形成了一张分层图，其中第\(i\)层的边集就是在以上构图方法中，第\(M+1-i\)步添加的边。不妨称序号大的层级为高层。

如果把第\(i\)层从点\(j\)到点\(k\)的边，画成平面上一条从\((j,i)\)到\((k,i)\)的线段，那么对第一个样例画出的图是：

注意到性质：高层线段的端点集合，一定是低层线段端点集合的子集；高层的线段，一定完整包含了低层对应位置的线段，且线段之间要么包含要么相离。

此外易见，对每一个\(i\)，存在点\(i\)作为端点的最高层级是\(l_i\)。

于是问题转化成，在这张分层图上，要从\((s,1)\)走到\((t,1)\)，允许以下两种转移，问最小代价：

1、如果点\(a\)是层级\(b\)和\(b+1\)的端点，则以代价\(0\)在\((a,b)\)与\((a,b+1)\)之间双向转移。

2、如果点\(a\)不是层级\(b\)中最靠左的端点，且在层级\(b\)中，点\(a\)左侧的相邻端点是\(c\)，则以代价\(1\)在\((a,b)\)与\((c,b)\)之间双向转移。

接下来就是喜闻乐见的推结论时间了！

结论1：一定有一条最优路径，满足其经过的层级高度是按访问顺序先增后减的。

证明：

考虑对于起终点相同，横坐标都单调递增（减）的两条路线\(A\)和\(B\)，如果\(A\)的高度始终不低于\(B\)，那么\(A\)经过的边数一定不大于\(B\)。

理由是：“高层的线段，一定完整包含了低层对应位置的线段”，所以走高层一定不会更差。

接下来考虑反证，假设这个路径的某一段形如下图的黑色路线：

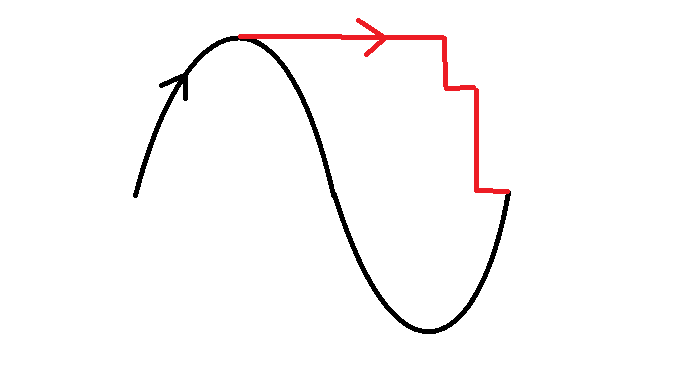
那么由先前结论，一定可以在达到最高点后改走红色路线，使答案不变得更差，同时保持凸性。

对于黑色路线横坐标不单调的情况，用类似方法可以证明同样的结论，有些繁琐，在此略去。

结论2：记\(L(a,b)\)为层级\(b\)中，点\(a\)左侧最近的端点（当\(a\)是端点时\(L(a,b)\)=\(a\)）；\(R(a,b)\)为层级\(b\)中，点\(a\)右侧最近的端点。那么，从\((a,1)\)到\(L(a,b)\)（或者\(R(a,b)\)）的最短路径，在第\(i\)层首次经过的点一定是\(L(a,i)\)或\(R(a,i)\)。

这个结论之后再证。

结论3：对\(s<t\)，从\((s,1)\)到\((t,1)\)的最短路径所经过的最大层级，要么是数组\(l\)在下标区间\([s,t]\)上的最大值\(Max\)，要么是\(Max+1\)。

对于结论2、3的证明：

考虑在下图中，当前位于点\(A\)，路径的起终点是第一层的\(s\)和\(t\)，且现在处于路径的上升阶段。

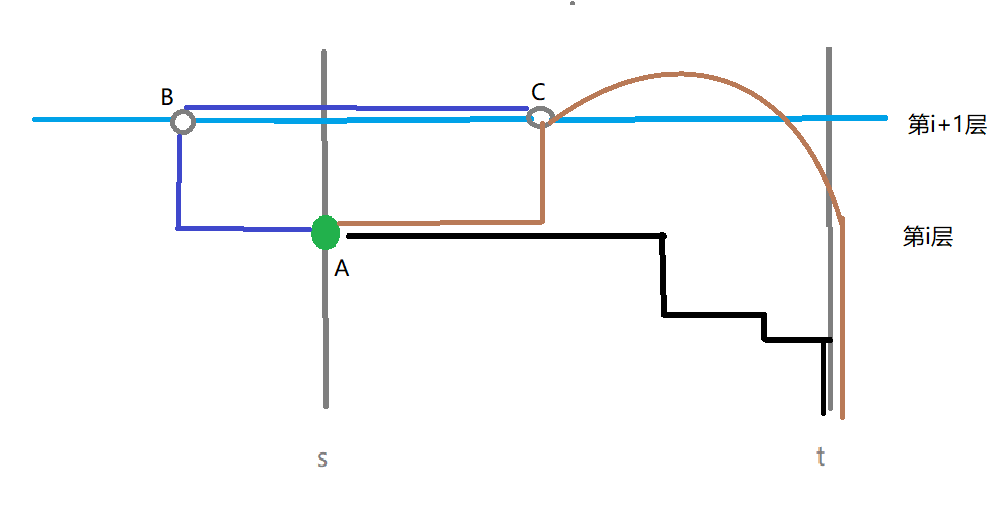
图中\(B=L(A,i+1)\)，\(C=R(A,i+1)\)。那么图中从\(A\)到\(t\)有以下几种可能的路径：

1、黑色路径：在第\(i\)层向右走直到横坐标超过\(C\)的横坐标，再沿着最优路径走到\(t\)。

2、褐色路径：在第\(i\)层向右走，再向上走到\(C\)，再沿着最优路径走到\(t\)。

3、深蓝+褐色路径：沿着深蓝色路径经过\(B\)走到\(C\)，再沿着褐色路径的后一半走到\(t\)。

对于起终点相同，横坐标都单调递增（减）的两条路线\(A\)和\(B\)，如果\(A\)的高度始终不低于\(B\)，那么\(A\)经过的边数一定不大于\(B\)。

所以，路径2一定不长于路径1。

换句话说，只要存在点\(C\)在\(i+1\)层，且\(C\)的横坐标在\(s\)和\(t\)之间，走到\(i+1\)层一定比留在第\(i\)层更优。

再换句话说，最短路径经过的最大层级，不小于\(Max\)。结论3的后一半之后再证。

接着考虑用数学归纳证明结论2。

归纳假设：最优路径在第\(i\)层首次经过的点一定是\(L(a,i)\)或\(R(a,i)\)。

当\(i=1\)时：易证。

当\(i=k\)时：

图中的\(A\)为\(L(a,k)\)或\(R(a,k)\)，则易知\(B=L(a,k+1)\)，\(C=R(a,k+1)\)。

对于在\(C\)右侧的\(C'\)，在第\(i+1\)层首次经过的点是\(C'\)的路径，一定是路径1，不是最优路径；

对于在\(B\)左侧的\(B'\)，如果一条路径在\(i+1\)首先经过的点是\(B'\)：

1°：如果到达\(B'\)后向右行走，则这条路径一定不优于图中的路径3（起终点相同，代价却更大）；

2°：如果到达\(B'\)后向左/上行走，易证，从\((B,k+2)\)向左走，一定能走到同样的第\(k+2\)层的结点，且代价不增加。

综上，在第\(k+1\)层经过的第一个点，必为\(B\)或\(C\)。

所以，如果\(i=k\)时命题成立，则对于\(i=k+1\)也成立。

结论2证毕。

由结论2可知，在最高层\(h\)，如果\(h>Max\)，在这一层一定只会走一步：从\(L(s,h)\)（或\(R(s,h)\)）到\(L(t,h)\)（或\(R(t,h)\)），代价恒为1。

又因为\(L(s,Max+2) \leq L(s,Max+1) , R(s,Max+2) \geq R(s,Max+1)\)（对\(t\)同理），所以\(h=Max+2\)时的代价不小于\(h=Max+1\)时的代价。

同理易证第\(Max+1\)层不比任何更高层更差。

所以最高层数不小于\(Max\)，不大于\(Max+1\)，结论3证毕。

呼……推完结论，终于开始设计算法了。

首先，回答查询的时候，显然应该枚举最高层级\(h\)（\(Max\)到\(Max+1\)），再把以下三个数相加：

1、\(s\)走到这一层的最小代价；

2、\(t\)走到这一层的最小代价；

3、\(s\)、\(t\)在这一层会合的最小代价；

（当然，\(s\)、\(t\)在最高层的首次访问位置是\(L(...,h)\)还是\(R(...,h)\)，还要对这个分四类讨论）

第三项很好求，在此只讲前两项的求法。

这种不断向一个方向跳的问题，不是一看就是倍增吗

考虑倍增，\(dp[i][j]\)表示从\((j,1)\)到\(L(j,2^i)\)和\(R(j,2^i)\)的距离？

等等，不对啊……这玩意怎么转移啊……

倍增算法可行的前提是，如果你把跳\(2^i\)步拆成跳两次\(2^{i-1}\)步，则前一步跳到的中继点，必须有一个状态来代表。

试了好几种比较裸的倍增方法，都不可行……看来得再分析一波了。

等等，其实我们关心的是\((i,1)\)与\(L(i,j)\)、\(R(i,j)\)之间的距离，而我们可以用二元组\(\{L(i,j),R(i,j)\}\)来代替状态中的\(i\)？

具体地说，这里，二元组\(\{L,R\}\)表示“当前所在位置的行（层级）不确定，（在结论2中的）列序号可以是\(L\)也可以是\(R\)”。

hint：注意每一个二元组都只在一个层级区间存在，即对于确定的\(\{L(i,j),R(i,j)\}\)，\(j\)的可能值是一个区间。

而且发现这种二元组只有\(O(N)\)个？

（证明方法，二元组数量就是构出的图中的不同的边数，而构图时每标记一个新点，最多产生两条新边。）

而且在不断往上跳的过程中，每一个二元组\(P\)的后继是唯一的？（后继是说，从\(P\)往上跳的过程中，达到的第一个与自己不相等的二元组）

而且只有在从二元组\(P\)跑到\(P\)的后继时才会产生代价？（也就是说同一个二元组代表的所有状态代价一样）

于是想到：\(dp[i][P]\)表示，从二元组\(P\)开始往上跳，所在的二元组改变\(2^i\)次（即当前在\(P\)的第\(2^i\)个后继）后的最小代价。

hint：注意\(dp[i][P]\)是两个值，分别表示到达二元组的左侧、右侧结点的代价。

前一步跳到的中继点，必须有一个状态来代表。

满足了吗？满足了。

啥？你说\(N^2 \log M\)大小的数组开不下？那是你的问题咯……好好想想怎么高效的把二元组放进状态里。

查询的时候沿着倍增指针不断地跳，直到当前二元组的存在区间囊括了目标层级为止。

总时间复杂度\(O((N+Q) \log M)\)。

接下来就是愉快的代码时间啦！

代码：

#include <bits/stdc++.h>
using namespace std;
#define iinf 2000000000
#define linf 1000000000000000000LL
#define ulinf 10000000000000000000ull
#define MOD1 1000000007LL
#define mpr make_pair
typedef long long LL;
typedef unsigned long long ULL;
typedef unsigned long UL;
typedef unsigned short US;
typedef pair < int , int > pii;
clock_t __stt;
inline void TStart(){__stt=clock();}
inline void TReport(){printf("\nTaken Time : %.3lf sec\n",(double)(clock()-__stt)/CLOCKS_PER_SEC);}
template < typename T > T MIN(T a,T b){return a<b?a:b;}
template < typename T > T MAX(T a,T b){return a>b?a:b;}
template < typename T > T ABS(T a){return a>0?a:(-a);}
template < typename T > void UMIN(T &a,T b){if(b<a) a=b;}
template < typename T > void UMAX(T &a,T b){if(b>a) a=b;}
const int lg=17,inf=1000000;
vector < int > prt[100005],lev[100005];
int n,m,q,l[100005],mx[lg][100005],dis[2][100005],nx[100005];
struct data{
	int ld,rd,lc,rc;
	void set(int LD,int RD,int LC,int RC){
		ld=LD;rd=RD;lc=LC;rc=RC;
		if(!ld) lc=inf;
	}
	void tran(data L,data R){
		if(L.ld==-1) L.lc=L.rc=inf;
		if(R.ld==-1) R.lc=R.rc=inf;
		int nlc=MIN(lc+L.lc,rc+R.lc),nrc=MIN(lc+L.rc,rc+R.rc);
		set((L.ld==-1?R.ld:L.ld),(L.ld==-1?R.rd:L.rd),nlc,nrc);
	}
};
vector < data > dp[lg][100005][2];
int prev(int i,int l){
	// before or equal
	int j;
	for(j=lg-1;j>=0;--j){
		if(i-(1<<j)>=-1 && mx[j][i-(1<<j)+1]<l){
			i-=(1<<j);
		}
	}
	return i;
}
int nxt(int i,int l){
	// after
	int j;
	++i;
	for(j=lg-1;j>=0;--j){
		if(i+(1<<j)<=n && mx[j][i]<l){
			i+=(1<<j);
		}
	}
	return i;
}
int qrymax(int l,int r){
	int le;
	for(le=0;(1<<(le+1))<r-l+1;++le);
	return MAX(mx[le][l],mx[le][r-(1<<le)+1]);
}
int qrydis(int s,int t,int le){
	int cnt=0;
	if(s>t) swap(s,t);
	while(s<t){
		if(le==l[s]){
			cnt+=dis[1][s]%inf;
			s=nxt(s,le+1);
		}
		else{
			++cnt;
			s=nxt(s,le);
		}
	}
	if(t<s && le==l[t]){
		cnt-=dis[1][t]%inf;
	}
	return cnt;
}
data qrydisV(int s,int le){
	data cur,nxt;
	if(s==n-1)
		cur.set(s-1,0,1,0);
	else
		cur.set(s,0,0,1);
	int i;
	for(i=lg-1;i>=0 && cur.ld!=-1;--i){
		nxt=cur;
		nxt.tran(dp[i][nxt.ld][0][nxt.rd],dp[i][nxt.ld][1][nxt.rd]);

		if(nxt.ld!=-1 && (nxt.rd?lev[nxt.ld][nxt.rd-1]:-1)<le)
			cur=nxt;
		if(cur.ld!=-1 && lev[cur.ld][cur.rd]>=le) break;
	}
	if(cur.ld!=-1 && lev[cur.ld][cur.rd]<le) cur.ld=-1;
	return cur;
}
int main(){
    // inputting start
    // 数据结构记得初始化！ n，m别写反！
    int i,j,k,fsv=-1,fsp=-1,scv=-1;
	scanf("%d%d%d",&n,&m,&q);
	for(i=1;i<=n;++i){
		scanf("%d",l+i);
		--l[i];
		if(l[i]>fsv){
			fsv=l[i];
			fsp=i;
		}
		else if(l[i]>scv){
			scv=l[i];
		}
	}
	l[fsp]=scv;
	l[0]=m++;
	++n;
    #ifdef LOCAL
        TStart();
    #endif
    // calculation start
    // 数据结构记得初始化！ n，m别写反！
	for(i=0;i<n;++i) mx[0][i]=l[i];
	for(i=1;i<lg;++i){
		for(j=0;j<n;++j){
			int nl=j+(1<<(i-1));
			if(nl<n)
				mx[i][j]=MAX(mx[i-1][j],mx[i-1][nl]);
			else
				mx[i][j]=mx[i-1][j];
		}
	}
	for(i=n-1;i>=0;--i){
		nx[i]=nxt(i,l[i]+1);
		int suc=nxt(i,l[i]);
		if(suc>=n)
			dis[1][i]=inf;
		else if(l[suc]>l[i])
			dis[1][i]=1;
		else
			dis[1][i]=dis[1][suc]+1;

		for(j=i+1;j<suc;j=nx[j]){
			prt[i].push_back(j);
			lev[i].push_back(l[j]);
		}
		if(suc<n){
			prt[i].push_back(suc);
			lev[i].push_back(l[i]);
		}

		dp[0][i][0].resize(prt[i].size());
		dp[0][i][1].resize(prt[i].size());
		for(j=0;j<(int)prt[i].size()-1;++j){
			dp[0][i][0][j].set(i,j+1,0,1);
			dp[0][i][1][j].set(i,j+1,1,MIN(2,dis[1][prt[i][j]]));
		}
	}
	for(i=0;i<n;++i){
		int prd=prev(i,l[i]+1),prv=prev(i-1,l[i]),d=(int)prt[i].size()-1;
		if(prv==-1)
			dis[0][i]=inf;
		else if(l[prv]>l[i])
			dis[0][i]=1;
		else
			dis[0][i]=dis[0][prv]+1;

		if(d==-1) continue;
		if(prd!=-1 && lev[prd].back()<=l[i]) prd=prev(prd-1,l[i]+1);

		if(prd==-1 || lev[prd].empty() || lev[prd].back()<=l[i])
			dp[0][i][0][d].ld=dp[0][i][1][d].ld=-1;
		else{
			int nd=lower_bound(lev[prd].begin(),lev[prd].end(),l[i]+1)-lev[prd].begin();
			int disL=dis[0][i],disR=dis[1][prt[i][d]];
			if(prt[i][d]==prt[prd][nd]) disR=0;

			dp[0][i][0][d].set(prd,nd,MIN(disL,disR+2),MIN(disL+1,disR+1));
			dp[0][i][1][d].set(prd,nd,MIN(disR+1,disL+1),MIN(disR,disL+2));
		}
	}
	for(i=1;i<lg;++i){
		for(j=0;j<n;++j){
			dp[i][j][0].resize(prt[j].size());
			dp[i][j][1].resize(prt[j].size());
			for(k=0;k<(int)prt[j].size();++k){
				int d;
				for(d=0;d<2;++d){
					data &trs=dp[i-1][j][d][k],&cur=dp[i][j][d][k];
					if(trs.ld==-1)
						cur.ld=-1;
					else{
						cur=trs;
						cur.tran(dp[i-1][cur.ld][0][cur.rd],dp[i-1][cur.ld][1][cur.rd]);
					}
				}
			}
		}
	}
    while(q--){
		int s[2];
		scanf("%d%d",s,s+1);
		sort(s,s+2);

		int mxl=qrymax(s[0],s[1]),res=inf;
		for(i=mxl;i<=mxl+1;++i){
			data tr[2];
			for(j=0;j<2;++j){
				tr[j]=qrydisV(s[j],i);
				if(tr[j].ld==-1) break;
			}
			if(j<2) break;

			int p[2],d[2];
			for(j=0;j<2;++j){
				p[0]=(j?prt[tr[0].ld][tr[0].rd]:tr[0].ld);
				d[0]=(j?tr[0].rc:tr[0].lc);
				for(k=0;k<2;++k){
					p[1]=(k?prt[tr[1].ld][tr[1].rd]:tr[1].ld);
					d[1]=(k?tr[1].rc:tr[1].lc);
					UMIN(res,d[0]+d[1]+qrydis(p[0],p[1],i));
				}
			}
		}
		printf("%d\n",res-1);
	}
    #ifdef LOCAL
        TReport();
    #endif
    return 0;
}