最小生成树 & 洛谷P3366【模板】最小生成树 & 洛谷P2820 局域网

嗯...

理解生成树的概念：

在一幅图中将所有n个点连接起来的n-1条边所形成的树。

最小生成树：

边权之和最小的生成树。

最小瓶颈生成树：

对于带权图，最大权值最小的生成树。

如何操作？

1.Prim算法（O（mlogn））

2.Kruskal算法（O（mlogn））

推荐使用第二种，无需建图。

算法流程：

Prim算法：（思想类似dijkstra）

　　随意选取一个点作为已访问集合的第一个点，并将所有相连的边加入堆中
　　从堆中找到最小的连接集合内和集合外点的边，将边加入最小生成树中
　　将集合外点标记为已访问，并将相连边加入堆
　　重复以上过程直到所有点都在访问集合中

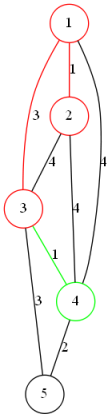
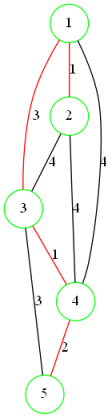
Kruskal算法：（并查集思想）

　　将边按照权值排序
　　依次枚举每一条边，若连接的两点不连通则加入最小生成树中
　　使用并查集维护连通性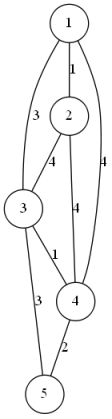

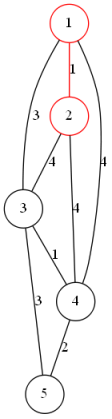
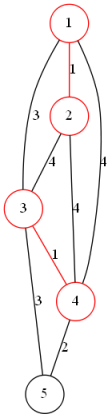
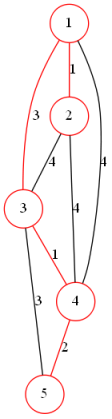
模板代码：

 int f[], h;
 struct node{
     int x, y, l;
 } a[];
 inline bool cmp(node i, node j){
     return i.l < j.l;
 }
 inline int find(int x){
     if(x != f[x])//本身是否为父亲节点
         f[x] = find(f[x]);
     return f[x];
 }//并查集操作
 int main(){
     for(int i = ; i <= n; i++){
         f[i] = i;
     }//父节点初始化
     sort(a+, a+k+, cmp);//排序
     for(int i = ; i <= k; i++){
         int r1 = find(a[i].x);
         int r2 = find(a[i].y);
         if(r1 != r2){
             f[r1] = r2;
         }
     }
 }

Kruskal

#include<bits/stdc++.h>
using namespace std;
int n,m,a,b,c;
int sum;
int g[][],minn[];
bool u[];
int main(){
    memset(g,0x7f,sizeof(g));
    memset(minn,0x7f,sizeof(minn));
    memset(u,true,sizeof(u));
    cin>>n>>m;
    for(int i=;i<=m;i++)
    {
        cin>>a>>b>>c;
        g[a][b]=g[b][a]=c;
        sum+=c;
    }
    minn[]=;
    for(int i=;i<=n;i++){
        int k=;
        for(int j=;j<=n;j++)
        if(u[j]&&minn[j]<minn[k])
        k=j;
        u[k]=false;
        for(int j=;j<=n;j++)
        if(u[j]&&g[k][j]<minn[j])
        minn[j]=g[k][j];
    }
    int total=;
    for(int i=;i<=n;i++)
    total+=minn[i];
    cout<<sum-total<<endl;
    return ;
}

Prim

---

模板题：

洛谷P3366【模板】最小生成树：

题目链接：https://www.luogu.org/problemnew/show/P3366

思路：（Kruskal）

一道模板题，首先用一个结构体读入，然后初始化父节点，再按边权排序，然后用find函数分别找输入时的两个点的父节点，并判断其中一个是否是另一个的父亲，否则就进行合并，并将h+=a[i].l。（思路比较好理解）

 #include<cstdio>
 #include<iostream>
 #include<algorithm>

 using namespace std;

 int h, f[];

 struct node{
     int x, y, l;
 } a[];

 inline bool cmp(node i, node j){
     return i.l < j.l;
 }

 inline int find(int x){
     if(x != f[x])
         f[x] = find(f[x]);
     return f[x];
 }

 int main(){
     int n, m;
     scanf("%d%d", &n, &m);
     for(int i = ; i <= n; i++){
         f[i] = i;
     }
     for(int i = ; i <= m; i++){
         scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].l);
         //h += a[i].l;
     }
     sort(a+, a+m+, cmp);
     for(int i = ; i <= m; i++){
         int r1 = find(a[i].x);
         int r2 = find(a[i].y);
         if(r1 != r2){
             f[r1] = r2;
             h += a[i].l;
             //h -= a[i].l;
         }
     }
     printf("%d", h);
     return ;
 }

AC代码

---

洛谷P2820 局域网：

题目链接：https://www.luogu.org/problemnew/show/P2820

思路：

首先这道题的问法就很模板：

很显然“f(i,j)表示i,j之间连接的畅通程度”即为i到j点的权值；“除去一些连线，使得网络中没有回路，并且被除去网线的Σf(i,j)最大”很显然是求最小生成树。但注意一个细节，它与最小生成树有所不同，它要求的是Σf(i,j)最大。

所以我们在最小生成树的模板上进行修改即可：读入时将所有的边权都加到h中。在判断父节点是否相同时，若不同，则将合并，并将合并的这条边的权值减掉即可。

 #include<cstdio>
 #include<iostream>
 #include<algorithm>

 using namespace std;

 int f[], h;

 struct node{
     int x, y, l;
 } a[];

 inline bool cmp(node i, node j){
     return i.l < j.l;
 }

 inline int find(int x){
     if(x != f[x])
         f[x] = find(f[x]);
     return f[x];
 }

 int main(){
     int n, k;
     scanf("%d%d", &n, &k);
     for(int i = ; i <= n; i++){
         f[i] = i;
     }
     for(int i = ; i <= k; i++){
         scanf("%d%d%d", &a[i].x, &a[i].y, &a[i].l);
         h += a[i].l;
     }
     sort(a+, a+k+, cmp);
     for(int i = ; i <= k; i++){
         int r1 = find(a[i].x);
         int r2 = find(a[i].y);
         if(r1 != r2){
             f[r1] = r2;
             h -= a[i].l;
         }
     }
     printf("%d", h);
     return ;
 }

AC代码

---

大概就是这样，个人认为Kruskal算法比Prim算法写起来简单并好理解....