SSH——增删改的实现一

在上一节介绍了关于BOS项目底层的查询操作，接下来介绍一下curd里的其他三项操作步骤

一、 取派员添加

利用easyui在staff.jsp页面里构造添加页面(相关JavaBean创建步骤省略)

    <div region="center" style="overflow:auto;padding:5px;" border="false">
            <form id="addStaffForm" action="${pageContext.request.contextPath }/staffAction_add.action"
                     method="post">
                <table class="table-edit" width="80%" align="center">
                    <tr class="title">
                        <td colspan="2">收派员信息</td>
                    </tr>

                    <tr>
                        <td>姓名</td>
                        <td><input type="text" name="name" class="easyui-validatebox" required="true"/></td>
                    </tr>
                    <tr>
                        <td>手机</td>
                        <td><input type="text" name="telephone" class="easyui-validatebox" required="true"
                            data-options="validType:'phonenumber'"
                        /></td>
                    </tr>
                    <tr>
                        <td>单位</td>
                        <td><input type="text" name="station" class="easyui-validatebox" required="true"/></td>
                    </tr>
                    <tr>
                        <td colspan="2">
                        <input type="checkbox" name="haspda" value="1" />
                        是否有PDA</td>
                    </tr>
                    <tr>
                        <td>取派标准</td>
                        <td>
                            <input type="text" name="standard" class="easyui-validatebox" required="true"/>
                        </td>
                    </tr>
                    </table>
            </form>
        </div>
    </div>

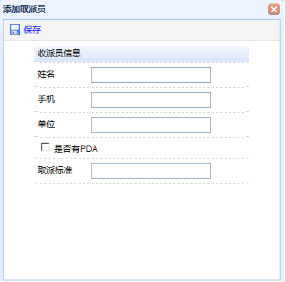
1. 增加很简单，所以这里拓展一下校验规则，对手机号进行一下校验

//扩展校验规则
    $(function(){
        var reg = /^1[3|4|5|7|8|9][0-9]{9}$/;
        $.extend($.fn.validatebox.defaults.rules, {
                phonenumber: {
                            validator: function(value, param){
                                return reg.test(value);
                            },
                            message: '手机号输入有误！'
                            }
                });
        });

2. 对应手机号输入框应用上面的规则

3. 为添加窗口中的保存按钮绑定事件

<a id="save" icon="icon-save" href="#" class="easyui-linkbutton" plain="true" >保存</a>
                <script type="text/javascript">
                    $(function(){
                        //绑定事件
                        $("#save").click(function(){
                            //校验表单输入项
                            var v = $("#addStaffForm").form("validate");
                            if(v){
                                //校验通过，提交表单
                                $("#addStaffForm").submit();
                            }
                        });
                    });
                </script>

4. 创建StaffAction，提供add方法，处理取派员添加

@Controller
@Scope("prototype")
public class StaffAction extends BaseAction<Staff>{
    //注入Service
    @Autowired
    private IStaffService staffService;
    /**
     * 添加取派员
     */
    public String add(){
        staffService.save(model);
        return "list";
    }
}

5. 配置struts.xml

<!-- 取派员管理 -->
        <action name="staffAction_*" class="staffAction" method="{1}">
            <result name="list">/WEB-INF/pages/base/staff.jsp</result>
        </action>

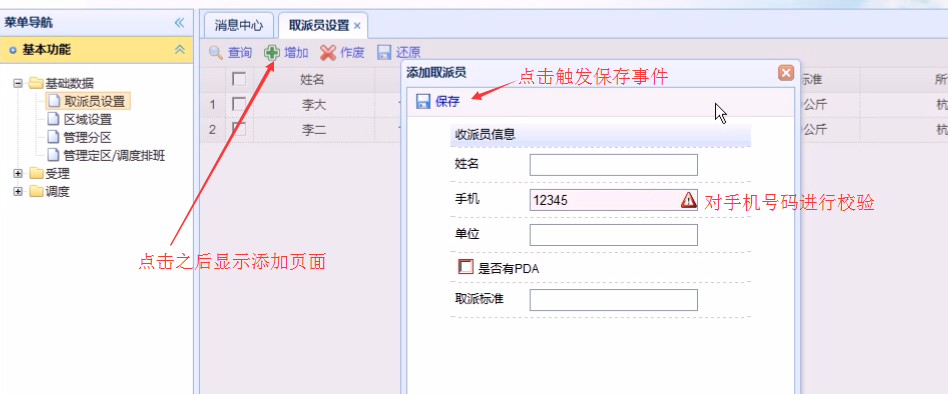
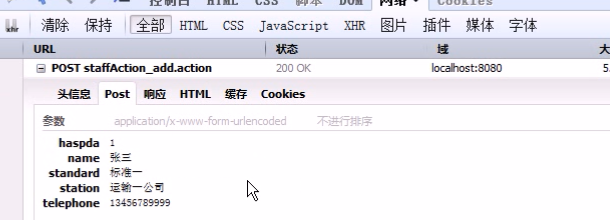
表单输入后点击保存可看到请求的信息

同时控制台输出  Hibernate： insert into...... 将信息添加进表中