【HDU5785】Interesting [Manacher]

Interesting

Time Limit: 30 Sec  Memory Limit: 256 MB
[Submit][Status][Discuss]

Description

　　

Input

　　

Output

　　

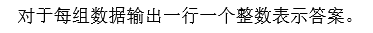
Sample Input

　　2
　　aaa
　　abc

Sample Output

　　14
　　8

HINT

　　

Source

　　我们先找一下这道题的本质，根据乘法分配律，我们可以使得：cntL[i]表示以 i 开始的是回文串的下标和，cntR[i]表示以 i 结束的回文串的下标和，那么这时候答案显然就是cntR[i]×cntL[i+1]。

　　我们再来思考一下怎么求出cntL和cntR，显然我们可以运用Manacher算法O(n)得到每一个回文半径，然后 i 对于cntL和cntR的影响显然就是一个序列上的等差数列。

　　接着我们再记录一下del表示公差，O(n)推一下等差数列每个位置的和即可。

Code

 #include<iostream>
 #include<string>
 #include<algorithm>
 #include<cstdio>
 #include<cstring>
 #include<cstdlib>
 #include<cmath>
 using namespace std;
 typedef long long s64;

 const int ONE = (1e6+)*;
 const int MOD = 1e9+;
 const int Niyu = 5e8+;

 int T;
 int cntL[ONE],delL[ONE],l;
 int cntR[ONE],delR[ONE],r;
 char s[ONE],a[ONE];
 int p[ONE],n;
 int Ans;

 int get()
 {
         int res=,Q=;  char c;
         while( (c=getchar())< || c>)
         if(c=='-')Q=-;
         if(Q) res=c-;
         while((c=getchar())>= && c<=)
         res=res*+c-;
         return res*Q;
 }

 void Deal_first()
 {
         a[] = '(';
         for(int i=;i<=n;i++)
         {
             a[*i-] = '#';
             a[*i] = s[i];
         }
         n =  * n + ;
         a[n] = '#';    a[n+] = ')';
 }

 void Manacher()
 {
         int l = , id = ;
         for(int i=;i<=n;i++) p[i] = ;
         for(int i=;i<=n;i++)
         {
             if(l >= i) p[i] = min(p[id + id - i], l - i);
             else p[i] = ;
             while(a[i-p[i]] == a[i+p[i]]) p[i]++;
             if(p[i] + i > l) l = p[i]+i, id = i;
         }
 }

 void Add(int &a,int b) {a+=b;    if(a>) a-=MOD;    if(a<) a+=MOD;}

 void Solve()
 {
         scanf("%s",s+);    n=strlen(s+);
         Deal_first();    Manacher();

         for(int i=;i<=n;i++) cntL[i]=cntR[i]=delL[i]=delR[i]=;

         for(int i=;i<=n;i++)
         {
             l = i-p[i]+;    r = i+p[i]-;
             Add(cntL[l], r);    Add(cntL[i+], -r+(i-l));    Add(delL[l+], -);    Add(delL[i+], );
             Add(cntR[i], i);    Add(cntR[r+], -i+(r-i));    Add(delR[i+], -);    Add(delR[r+], );
         }

         for(int i=;i<=n;i++)
         {
             Add(cntL[i],cntL[i-]);    Add(delL[i],delL[i-]);    Add(cntL[i],delL[i]);
             Add(cntR[i],cntR[i-]);    Add(delR[i],delR[i-]);    Add(cntR[i],delR[i]);
         }

         n=strlen(s+);
         Ans = ;
         for(int i=;i<n;i++)
         {
             Ans = Ans + (s64)cntR[*i] *Niyu%MOD * cntL[*(i+)]%MOD *Niyu%MOD ;
             Add(Ans,);
         }

         printf("%d\n",Ans);
 }

 int main()
 {
         T=get();
         while(T--)
             Solve();
 }