曲率（Curvature）

原文链接

几何体的曲率对于不同的对象有不同的定义。首先来看最简单的平面曲线。

首先把曲线分成无穷小的小段，每一段看作某个圆的一小段圆弧。这个圆叫做“密切圆”（Osculating Circle）。由于它与曲线只相交于极小的一段，又称为“接吻圆”（Kissing Circle）。这个圆的半径称为“曲率半径”。

“曲率”是一个向量，它从圆弧上的参考点指向密切圆圆心。密切圆曲率半径的倒数就是这个圆弧在这个点上“曲率”的大小。

所以，曲线越接近直线，曲率半径就越大，在这一点上的曲率就越小。直线曲率处处为零。

曲率大小的单位是“屈光度”（Dioptre）,等于每米的弧度。以透镜为例，屈光度为2的透镜会把光线聚焦在距离镜片的0.5米处。有时候用+表示凸透镜，-表示凹透镜。在眼镜制造中，通常忽略负号，并用曲率的100倍为“度数”。比如，屈光度为-2的眼镜片被称作200度的眼镜片。

曲率的数学定义是曲线上极小的一段AB之间的切线变化程度比上曲线的弧长：

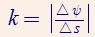
其中，设曲线为

另一方面，对于弧长有：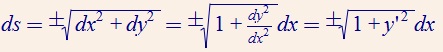

全部带如原式得：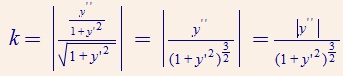

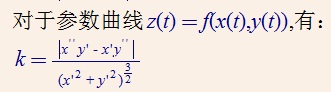
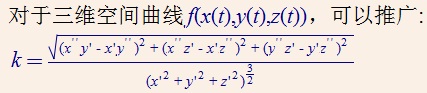
曲面的曲率

曲面的曲率可以由曲线的曲率推导出来。设在欧几里德空间中存在一个三维曲面，规定过某点的曲率为过该点的法向量和某一切向量所确定的平面的交集（是一条曲线）的曲率。由于过某点可以确定无数条曲线，所以定义曲面的两条主曲率（Principal curvatures）为交集中曲线的最大曲率k1和最小曲率k2。主曲率衡量了曲面在某点上最大和最小的弯曲程度，具有代表意义。

两个主曲率的平均值称为平均曲率（Mean curvature），两个主曲率的乘积称为高斯曲率(Gaussian curvature)。平均曲率描述的是某一点的曲面“嵌入”周围环境的程度。高斯曲率描述的是“内在量度”（Intrinsic measure）。根据高斯绝妙定理（Theorema Egregium）,曲面的高斯曲率可以并仅由角度、长度的测量来决定。