Dijkstra单源最短路径，POJ(2387)

题目链接:http://poj.org/problem?id=2387

Dijkstra算法：　　　　//求某一点(源点)到另一点的最短路，算法其实也和源点到所有点的时间复杂度一样，O(n^2);

图G(V,E),设置一个顶点集合S，不断贪心选择，指导S扩充为V,计算结束。

贪心选择的方法：节点个数n，源节点v，先在S中加入源节点v，初始化源节点，开始扩充S，找到一个点，他离S集合最近，加入到S集合中去，再利用这个点更新S本身中的最短路径。

题目大意：很裸的Dijkstra，但是这里有两点

1、图是双向的，存图的时候存双向图。

2、有重边，两个点之间有多条边，不断更新

模板：

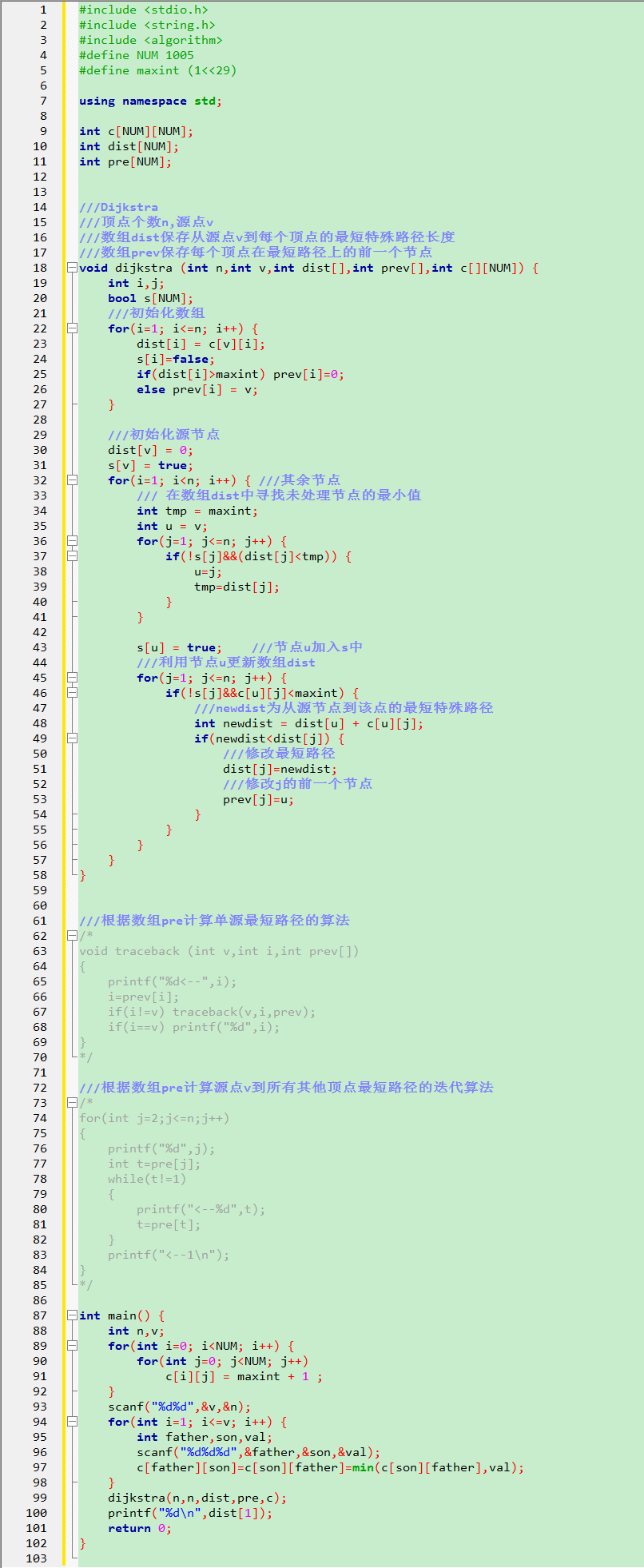
#include <stdio.h>
#include <string.h>
#include <algorithm>
#define NUM 1005
#define maxint (1<<29)

using namespace std;

int c[NUM][NUM];
int dist[NUM];
int pre[NUM];

///Dijkstra
///顶点个数n,源点v
///数组dist保存从源点v到每个顶点的最短特殊路径长度
///数组prev保存每个顶点在最短路径上的前一个节点
void dijkstra (int n,int v,int dist[],int prev[],int c[][NUM])
{
    int i,j;
    bool s[NUM];
    ///初始化数组
    for(i=; i<=n; i++)
    {
        dist[i] = c[v][i];
        s[i]=false;
        if(dist[i]>maxint) prev[i]=;
        else prev[i] = v;
    }

    ///初始化源节点
    dist[v] = ;
    s[v] = true;
    for(i=; i<n; i++)   ///其余节点
    {
        /// 在数组dist中寻找未处理节点的最小值
        int tmp = maxint;
        int u = v;
        for(j=; j<=n; j++)
        {
            if(!s[j]&&(dist[j]<tmp))
            {
                u=j;
                tmp=dist[j];
            }
        }

        s[u] = true;    ///节点u加入s中
        ///利用节点u更新数组dist
        for(j=; j<=n; j++)
        {
            if(!s[j]&&c[u][j]<maxint)
            {
                ///newdist为从源节点到该点的最短特殊路径
                int newdist = dist[u] + c[u][j];
                if(newdist<dist[j])
                {
                    ///修改最短路径
                    dist[j]=newdist;
                    ///修改j的前一个节点
                    prev[j]=u;
                }
            }
        }
    }
}

///根据数组pre计算单源最短路径的算法
/*
void traceback (int v,int i,int prev[])
{
    printf("%d<--",i);
    i=prev[i];
    if(i!=v) traceback(v,i,prev);
    if(i==v) printf("%d",i);
}
*/

///根据数组pre计算源点v到所有其他顶点最短路径的迭代算法
/*
for(int j=2;j<=n;j++)
{
    printf("%d",j);
    int t=pre[j];
    while(t!=1)
    {
        printf("<--%d",t);
        t=pre[t];
    }
    printf("<--1\n");
}
*/

int main()
{
    int n,v;
    for(int i=; i<NUM; i++)
    {
        for(int j=; j<NUM; j++)
            c[i][j] = maxint +  ;
    }
    scanf("%d%d",&v,&n);
    for(int i=; i<=v; i++)
    {
        int father,son,val;
        scanf("%d%d%d",&father,&son,&val);
        c[father][son]=c[son][father]=min(c[son][father],val);
    }
    dijkstra(n,n,dist,pre,c);
    printf("%d\n",dist[]);
    return ;
}