acm数论之旅--欧拉函数的证明

随笔 - 20  文章 - 0  评论 - 73

ACM数论之旅7---欧拉函数的证明及代码实现（我会证明都是骗人的╮(￣▽￣)╭）

https://blog.csdn.net/chen_ze_hua/article/details/53997790

https://blog.csdn.net/qq_40828914/article/details/81775519

欧拉函数，用φ(n)表示

欧拉函数是求小于等于n的数中与n互质的数的数目

辣么，怎么求哩？~(～o￣▽￣)～o

可以先在1到n-1中找到与n不互质的数，然后把他们减掉

比如φ(12)

把12质因数分解，12=2*2*3，其实就是得到了2和3两个质因数

然后把2的倍数和3的倍数都删掉

2的倍数：2,4,6,8,10,12

3的倍数：3,6,9,12

本来想直接用12 - 12/2 - 12/3

但是6和12重复减了

所以还要把即是2的倍数又是3的倍数的数加回来 (＞﹏＜)

所以这样写12 - 12/2 - 12/3 + 12/(2*3)

这叫什么，这叫容斥啊，容斥定理听过吧

比如φ(30)，30 = 2*3*5

所以φ(30) = 30 - 30/2 - 30/3 - 30/5 + 30/(2*3) + 30/(2*5) + 30/(3*5) - 30/(2*3*5)

但是容斥写起来好麻烦(￣.￣)

有一种简单的方法

φ(12)   =   12*(1 - 1/2)*(1 - 1/3)                 =   12*(1 - 1/2 - 1/3 + 1/6)

φ(30)   =   30*(1 - 1/2)*(1 - 1/3)*(1 - 1/5)   =   30*(1 - 1/2 - 1/3 - 1/5 + 1/6 + 1/10 + 1/15 - 1/30)

你看( •̀∀•́ )，拆开后发现它帮你自动帮你容斥好

所以φ(30)的计算方法就是先找30的质因数

分别是2,3,5

然后用30* 1/2 * 2/3 * 4/5就搞定了

顺便一提，phi(1) = 1

代码如下：

 1 //欧拉函数
 2 int phi(int x){
 3     int ans = x;
 4     for(int i = 2; i*i <= x; i++){
 5         if(x % i == 0){
 6             ans = ans / i * (i-1);
 7             while(x % i == 0) x /= i;
 8         }
 9     }
10     if(x > 1) ans = ans / x * (x-1);
11     return ans;
12 }

（phi就是φ的读音）

机智的代码，机智的我(｡・`ω´･)

这个的复杂度是O（√n），如果要你求n个数的欧拉函数，复杂度是O（n√n），这也太慢了

有更快的方法

跟埃筛素数差不多

 1 #include<cstdio>
 2 const int N = 100000 + 5;
 3 int phi[N];
 4 void Euler(){
 5     phi[1] = 1;
 6     for(int i = 2; i < N; i ++){
 7         if(!phi[i]){
 8             for(int j = i; j < N; j += i){
 9                 if(!phi[j]) phi[j] = j;
10                 phi[j] = phi[j] / i * (i-1);
11             }
12         }
13     }
14 }
15 int main(){
16     Euler();
17 }

（Euler就是欧拉）

另一种，比上面更快的方法

需要用到如下性质

p为质数

1. phi(p)=p-1   因为质数p除了1以外的因数只有p，故1至p的整数只有p与p不互质

2. 如果i mod p = 0, 那么 phi(i * p)=phi(i) * p         （我不会证明）

3.若i mod p ≠0,  那么 phi( i * p )=phi(i) * ( p-1 )   （我不会证明）

（所以我说我会证明都是骗人的╮(￣▽￣)╭）

代码如下：

1 #include<cstdio>

 2 using namespace std;
 3 const int N = 1e6+10 ;
 4 int phi[N], prime[N];
 5 int tot;//tot计数，表示prime[N]中有多少质数
 6 void Euler(){
 7     phi[1] = 1;
 8     for(int i = 2; i < N; i ++){
 9         if(!phi[i]){
10             phi[i] = i-1;
11             prime[tot ++] = i;
12         }
13         for(int j = 0; j < tot && 1ll*i*prime[j] < N; j ++){
14             if(i % prime[j]) phi[i * prime[j]] = phi[i] * (prime[j]-1);
15             else{
16                 phi[i * prime[j] ] = phi[i] * prime[j];
17                 break;
18             }
19         }
20     }
21 }
22
23 int main(){
24     Euler();//先初始化为零
25 }

最后说下

a^b % p  不等价  (a%p)^(b%p) % p

因为

a^φ(p) ≡ 1 (mod p)

所以

a^b % p  =  (a%p)^(b%φ(p)) % p

（欧拉函数前提是a和p互质）

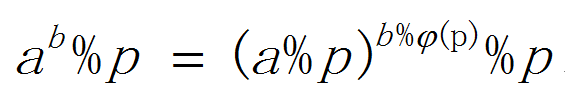
如果p是质数

直接用这个公式

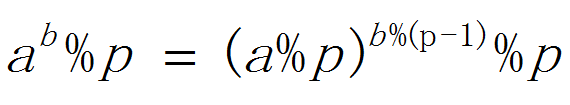
机智的代码，机智的我(｡・`ω´･)

///////////////////////////////////////////////

2016年7月23号

我的天哪，我又发现了一个新公式，貌似可以摆脱a和p互质的束缚，让我们来命名为：超欧拉取模进化公式

a^b = a^( b % phi(m) + phi(m) ) ( mod m )，这个公式的前提条件是 b >= phi(m)

这是历史性的一刻，妈妈再也不用为a和p不互质而担心了= =

Huge Mods

UVA - 10692

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;
const int maxm = 1e4 + ;
int m, n;
char ch[];
int  a[], phi[maxm];
void Euler(){
    phi[] = ;
    for(int i = ; i < maxm; i ++){
        if(!phi[i]){
            for(int j = i; j < maxm; j += i){
                if(!phi[j]) phi[j] = j;
                phi[j] = phi[j] / i * (i-);
            }
        }
    }
}
int qpow(int x, int b, int mod) {
    int res = ;
    while (b > ) {
        if (b & ) {
            res = res * x % mod;
        }
        x = x * x % mod;
        b >>= ;
    }
    return res;
}
int solve(int d, int m) {
if(d == n - ) return a[d] % m;
int x = phi[m] + solve(d + , phi[m]);
//关键，主要是除phi[m].
return qpow(a[d], x, m) % m;
}
int t;
int main() {
Euler();
while(~scanf("%s", ch)) {
    if(ch[] == '#') break;
    sscanf(ch, "%d", &m);
    scanf("%d", &n);
    for(int i = ; i < n; i++) {
        scanf("%d", &a[i]);
    }
//    if(n == 1) printf("Case #%d: %d\n", ++t, n );
//    else
    printf("Case #%d: %d\n", ++t, solve(, m));
}
return ;
}