T2963 贪吃蛇【BFS，四进制状压，A*】

Online Judge：未知

Label：BFS，四进制状压，暴力，A*，哈希，玄学。

题目描述

给定一个n*m的地图和蛇的初始位置，地图中有些位置有石头，蛇不能经过。当然蛇也不能爬到地图之外。

每次移动，蛇头先动，接下来每节身体到达上一节身体所在的位置。蛇头将要去的地方，不能有身体的其他部分。

求蛇最少移动多少步到达（1,1）点。

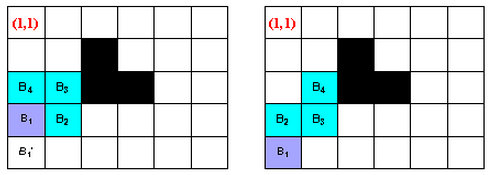
下图B1是蛇头，B4是蛇尾，第二幅图是第一幅图蛇移动一步之后的效果,黑色区域是石头。

输入

第一行3个整数n、m、K，K表示蛇的长度。

接下来K行，每行两个整数，表示蛇每节身体的坐标，依次从蛇头到蛇蛇尾，坐标为行号和列号。

第K+2行一个整数s，表示石头的个数。接下来s行，每行两个整数，表示一个石头的行号和列号。石头不会出现在（1,1）。

输出

输出蛇头最少多少步，可以到达（1,1）点。如果无法到达，输出-1。

样例

Input

Output

Hint

对于30%的数据，K=1;

对于60%的数据，1≤K≤3,n和m的范围[2,10];

对于100%的数据，1≤K≤8,n和m的范围[2,20];

题解

由于n,m同阶，下面描述算法时间复杂度时统一用n。

30pts

就是普通的BFS。时间复杂度为\(O(N^2)\)。

#include<bits/stdc++.h>

using namespace std;

const int dx[]={-1,1,0,0};

const int dy[]={0,0,-1,1};

int n,m,k,mark[22][22];

struct node{int x,y;};

queue<node>q;

namespace p30{

    int dis[22][22];

    void bfs(int sx,int sy){

        for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)dis[i][j]=-1;

        q.push((node){sx,sy});

        dis[sx][sy]=0;

        while(!q.empty()){

            node now=q.front();q.pop();

            int x=now.x,y=now.y;

            if(x==1&&y==1)break;

            for(int i=0;i<=3;i++){

                int nx=x+dx[i],ny=y+dy[i];

                if(nx<1||ny<1||nx>n||ny>m||mark[nx][ny])continue;

                if(dis[nx][ny]==-1){

                    dis[nx][ny]=dis[x][y]+1;

                    q.push((node){nx,ny});

                }

            }

        }

        printf("%d\n",dis[1][1]);

    }

    void solve(){

        int sx,sy;scanf("%d%d",&sx,&sy);

        for(int i=1;i<k;i++){

            int x,y;scanf("%d%d",&x,&y);

        }

        int tmp;scanf("%d",&tmp);

        for(int i=1;i<=tmp;i++){

            int x,y;scanf("%d%d",&x,&y);

            mark[x][y]=1;

        }

        bfs(sx,sy);

    }

}

int main(){

    scanf("%d%d%d",&n,&m,&k);

    p30::solve();

}

60pts

由于身体最多只有三段。状态可以直接记录每段的位置\([x1][y1][x2][y2][x3][y3]\)。转移的话直接暴力把身子的坐标挪一下。

上面空间看起来比较悬，所以不要直接用\(dis[x1][y1][x2][y2][x3][y3]\)这个数组，在结构体里搞。

struct node{int x[3],y[3];};

由于广搜用到的状态应该不会太多，空间上不太可能会被卡掉。而时间上大致为\(O(N^k )=O(N^6)\)。

//如果把下面结构体里的x[],y[]开大，其实可以过掉这道题qwq。

#include<bits/stdc++.h>

using namespace std;

const int rx[]={-1,1,0,0},ry[]={0,0,-1,1};

int n,m,k,s;

bool mark[25][25];

struct node{

    int x[3],y[3],step;

}A;

queue<node>Q;

bool check(int x,int y){

    return x>=1&&x<=n&&y>=1&&y<=m&&!mark[x][y];

}

int bfs(){

    Q.push(A);

    node now,nxt;

    while(!Q.empty()){

        now=Q.front();

        Q.pop();

        if(now.x[0]==1&&now.y[0]==1)return now.step;

        for(int i=0;i<4;i++){

            bool flag=0;

            int X=now.x[0]+rx[i],Y=now.y[0]+ry[i];

            for(int j=0;j<k;j++)

                if(X==now.x[j]&&Y==now.y[j])flag=1;

            if(flag)continue;

            if(check(X,Y)){

                for(int j=1;j<k;j++){

                    nxt.x[j]=now.x[j-1];

                    nxt.y[j]=now.y[j-1];

                }

                nxt.step=now.step+1;

                nxt.x[0]=X,nxt.y[0]=Y;

                Q.push(nxt);

                mark[X][Y]=1;

            }

        }

    }

    return -1;

}

int main(){

    scanf("%d%d%d",&n,&m,&k);

    for(int i=0;i<k;i++)scanf("%d%d",&A.x[i],&A.y[i]);

    scanf("%d",&s);

    for(int i=1;i<=s;i++){

        int x,y;

        scanf("%d%d",&x,&y);

        mark[x][y]=1;

    }

    A.step=0;

    mark[A.x[0]][A.y[0]]=1;

    printf("%d\n",bfs());

    return 0;

}

100pts

如果上面的结构体里数组开成k=8，再哈希一下或用A*之类的去优化，也可以过，而且比下面的解法还快。

记录每段身子的坐标太费空间了。

观察到身子是连着的(废话)，所以可以像这样去记录，第二段在第一段的哪个方位。这样只有四个方向，可以用四进制状压。

下面代码中：i在i+1左边：0，i在i+1上边：1，i在i+1右边：2，i在i+1下边：3。

BFS仍然是BFS，主要转移上会有点麻烦，注意细节。

代码如下:

/*

  1

0[]2

 3

*/

#include<bits/stdc++.h>

#define N 22

using namespace std;

const int dx[]={-1,1,0,0},dy[]={0,0,-1,1},Turn[]={3,1,2,0};

int n,m,k,mark[N][N];

int pw[10],dis[N][N][16500];

inline int gonxt(int S,int di){return S*4%pw[k-1]+Turn[di];}

//移动后，更新状态

inline bool boom(int x,int y,int S,int di){

//会撞到自己时返回1

	int nx=x+dx[di],ny=y+dy[di];

	for(register int i=1;i<k;++i){

		int o=S-S/4*4;S/=4;

		if(o==0)y--;if(o==1)x--;if(o==2)y++;if(o==3)x++;

		if(x==nx&&y==ny)return 1;

	}

	return 0;

}

struct node{int x,y,S;}q[6600000];

inline int bfs(int sx,int sy,int fir){

	memset(dis,-1,sizeof(dis));

	int head=1,tail=0;

	q[++tail]=((node){sx,sy,fir});dis[sx][sy][fir]=0;

	while(head<=tail){

		node now=q[head];head++;

		int x=now.x,y=now.y,S=now.S;

		if(x==1&&y==1)return dis[x][y][S];

		for(register int i=0;i<=3;++i){

			int nx=x+dx[i],ny=y+dy[i];

			if(nx<1||ny<1||nx>n||ny>m||mark[nx][ny]||boom(x,y,S,i))continue;

			int T=gonxt(S,i);

			if(dis[nx][ny][T]==-1){

				dis[nx][ny][T]=dis[x][y][S]+1;

				q[++tail]=(node){nx,ny,T};

			}

		}

	}

	return -1;

}

int main(){

	register int sx,sy,x,y,lstx,lsty,S=0,tmp,i,v[9];

	scanf("%d%d%d",&n,&m,&k);

	pw[0]=1;

	for(i=1;i<=9;++i)pw[i]=pw[i-1]*4;

	scanf("%d%d",&sx,&sy);lstx=sx,lsty=sy;

	for(i=1;i<k;++i){

		scanf("%d%d",&x,&y);

		if(x!=lstx)v[i]=(x==lstx-1)?1:3;

		else v[i]=(y==lsty-1)?0:2;

		lstx=x,lsty=y;

	}

	for(i=k-1;i>=1;i--)S=S*4+v[i];

	//初始状态(sx,sy,S)

	scanf("%d",&tmp);

	for(i=1;i<=tmp;++i)scanf("%d%d",&x,&y),mark[x][y]=1;

	cout<<bfs(sx,sy,S);

}