PTA Is Topological Order

Write a program to test if a give sequence Seq is a topological order of a given graph Graph.

Format of functions:

bool IsTopSeq( LGraph Graph, Vertex Seq[] );

where LGraph is defined as the following:

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

The function IsTopSeq must return true if Seq does correspond to a topological order; otherwise return false.

Note: Although the vertices are numbered from 1 to MaxVertexNum, they are indexed from 0 in the LGraph structure.

Sample program of judge:

#include <stdio.h>
#include <stdlib.h>

typedef enum {false, true} bool;
#define MaxVertexNum 10  /* maximum number of vertices */
typedef int Vertex;      /* vertices are numbered from 1 to MaxVertexNum */

typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};

typedef struct Vnode{
    PtrToAdjVNode FirstEdge;
} AdjList[MaxVertexNum];

typedef struct GNode *PtrToGNode;
struct GNode{
    int Nv;
    int Ne;
    AdjList G;
};
typedef PtrToGNode LGraph;

LGraph ReadG(); /* details omitted */

bool IsTopSeq( LGraph Graph, Vertex Seq[] );

int main()
{
    int i, j, N;
    Vertex Seq[MaxVertexNum];
    LGraph G = ReadG();
    scanf("%d", &N);
    for (i=; i<N; i++) {
        for (j=; j<G->Nv; j++)
            scanf("%d", &Seq[j]);
        if ( IsTopSeq(G, Seq)==true ) printf("yes\n");
        else printf("no\n");
    }

    return ;
}

/* Your function will be put here */

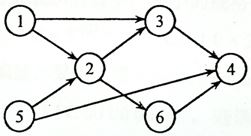
Sample Input (for the graph shown in the figure):

Sample Output:

yes
yes
yes
no
no

题目的大致意思就是，给你一组数据，根据这组数据构建一个有向图，再给你几组序列，判断是不是拓扑序列。

思路：先确定每个结点的入度数，按拓扑顺序输出结点时，每输出一个结点，将其子结点的入度数 -1.

注意：输入的顶点是从 0 开始存放的，也就是

0	1	2	3	4
G1	G2	G3	G4	G5

struct AdjVNode{
    Vertex AdjV;
    PtrToAdjVNode Next;
};
中的 AdjV，也是从 0 开始存放。

代码：

bool IsTopSeq( LGraph Graph, Vertex Seq[] ){
    int inDegree[];
    for(int i=;i<=Graph->Nv;i++)
        inDegree[i]=;
    PtrToAdjVNode temnode;
    for(int i=;i<Graph->Nv;i++){
        temnode=Graph->G[i].FirstEdge;
        while (temnode){
            inDegree[temnode->AdjV]++;
            temnode=temnode->Next;
        }
    } 
    for(int i=;i<Graph->Nv;i++){
        if(inDegree[Seq[i]-]!=)
            return false;
        else{
            temnode=Graph->G[Seq[i]-].FirstEdge;
            while(temnode){
                inDegree[temnode->AdjV]--;
                temnode=temnode->Next;
            }
        }
    }
    return true;
}