Codeforces 922 E Birds （背包dp）被define坑了的一题

网页链接：点击打开链接

Apart from plush toys, Imp is a huge fan of little yellow birds!

To summon birds, Imp needs strong magic. There are n trees in a row on an alley in a park, there is a nest on each of the trees. In the i-th nest there are ci birds; to summon one bird from this nest Imp needs to stay under this tree and it costs him costi points of mana. However, for each bird summoned, Imp increases his mana capacity by B points. Imp summons birds one by one, he can summon any number from 0 to ci birds from the i-th nest.

Initially Imp stands under the first tree and has W points of mana, and his mana capacity equals W as well. He can only go forward, and each time he moves from a tree to the next one, he restores X points of mana (but it can't exceed his current mana capacity). Moving only forward, what is the maximum number of birds Imp can summon?

Input

The first line contains four integers n, W, B, X (1 ≤ n ≤ 103, 0 ≤ W, B, X ≤ 109) — the number of trees, the initial points of mana, the number of points the mana capacity increases after a bird is summoned, and the number of points restored when Imp moves from a tree to the next one.

The second line contains n integers c1, c2, ..., cn (0 ≤ ci ≤ 104) — where ci is the number of birds living in the i-th nest. It is guaranteed that .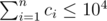

The third line contains n integers cost1, cost2, ..., costn (0 ≤ costi ≤ 109), where costi is the mana cost to summon a bird from the i-th nest.

Output

Print a single integer — the maximum number of birds Imp can summon.

Examples

input

Copy

2 12 0 4
3 4
4 2

output

6

input

Copy

4 1000 10 35
1 2 4 5
1000 500 250 200

output

5

input

Copy

2 10 7 11
2 10
6 1

output

11

Note

In the first sample base amount of Imp's mana is equal to 12 (with maximum capacity also equal to 12). After he summons two birds from the first nest, he loses 8 mana points, although his maximum capacity will not increase (since B = 0). After this step his mana will be 4 of 12; during the move you will replenish 4 mana points, and hence own 8 mana out of 12 possible. Now it's optimal to take 4 birds from the second nest and spend 8 mana. The final answer will be — 6.

In the second sample the base amount of mana is equal to 1000. The right choice will be to simply pick all birds from the last nest. Note that Imp's mana doesn't restore while moving because it's initially full.

题目大意：一共有n棵树，刚开始有w元，第i棵树上有nb[i]只鸟，第i棵树上的鸟要花c[i]元，每走一棵树增加x元，每买一个鸟会让钱包容量增加b，问最多能买到几只鸟？

解法：背包dp，不过这题要根据数据范围选好下标，下标不能是1e9的钱数，dp的值不能是鸟数，鸟数可以用来当成下标

dp[i][j]表示走到第i棵树下，这时候已经买了j只鸟，剩下的钱数,dp[i][j] = max{dp[i-1][j - k] - k * c[i-1] + x}

坑点：每次更新dp[i][j]的时候钱不能超过钱包容量，而且要算出买几只鸟能让dp[i][j]最大，所以用了个嵌套的max,min，但是！！我居然学别人在开头define了max和min，导致嵌套了个寂寞，以后要么自己定义函数，要么直接用algorithm中的max，别再define了！

代码里还是有蛮多细节技巧的，仔细看看

#include<cstdio>
#include<cstring>
#include<algorithm>
//#define min(a, b) a>=b?b:a   //←罪魁祸首！！！
//#define max(a, b) a>=b?a:b   //←你也是！！！！
typedef long long ll;
using namespace std;

const int maxn = 1000 + 100;
const int maxw = 10000 + 100;
ll c[maxn], nb[maxw];
ll dp[maxn][maxw];//dp[i][j]表示走到第i棵树下，这时候已经买了j只鸟，剩下的钱数
//dp[i][j] = max{dp[i-1][j - k] - k * c[i-1] + x}

int main(){
    ll n, w, b, x;//走一棵树加x钱，买一只鸟增加容量b;
	scanf("%lld %lld %lld %lld", &n, &w, &b, &x);
	int mana = w, max_mana = w;
	for(int i = 0; i < n; i++) scanf("%d", &nb[i]);
	for(int i = 0; i < n; i++) scanf("%d", &c[i]);
	ll sum = 0;
	memset(dp, -1, sizeof(dp));//最后还为-1的dp就是不可能达到的
	dp[0][0] = w;//当i等于0的时候，即在第一棵树下的时候，这时候一只鸟都没买，所以当i=0时只有j=0这种情况
	for(int i = 1; i <= n; i++){//从刚到第二棵树下开始循环（正在第二颗树下，还没决定在第二颗树买几只鸟）
		sum += nb[i-1];//此时站在第i棵树下，最多买了sum只鸟，也就是前面的全买了 

		for(int j = 0; j <= sum; j++){
			for(int k = 0; k <= nb[i-1] && k <= j ; k++){//这个循环用来解决dp[i][j]的最大值能是多少
			    if(dp[i-1][j-k] == -1){/*printf("j = %d, k = %d, dp[%d][%d] = %d\n", j, k, i-1, j-k,dp[i-1][j-k]);*/continue;}
				if(dp[i-1][j-k] - k * c[i-1] < 0 ) {/*printf("nonono!\nk = %d, j = %d\n", k, j);*/continue;}//没钱了, 这时候还没走到下一棵树，所以不要加x
				dp[i][j] = max(dp[i][j], min(dp[i-1][j-k] - k*c[i-1] + x, w + j * b));//更新最大的dp,同时注意钱包的上限
				//printf("dp[i-1][j-k] - k*c[i-1] + x为%d\n此时w+j*b为%d, dp[%d][%d]应该为%d\n", dp[i-1][j-k] - k*c[i-1] + x,w+j*b, i, j, min(dp[i-1][j-k] - k*c[i-1] + x, w + j * b));
			}
			 //printf("dp[%d][%d] = %d, sum = %d\n", i, j, dp[i][j], sum);
		}

	}
	ll ans;
	for(int i = 0; i <= sum; i++)
        if(dp[n][i] != -1) ans = i;
    printf("%lld\n", ans);
	return 0;
}