用C#表达式树优雅的计算24点

思路：一共4个数字，共需要3个运算符，可以构造一个二叉树，没有子节点的节点的为值，有叶子节点的为运算符

例如数字{1, 2, 3, 4}，其中一种解的二叉树形式如下所示：

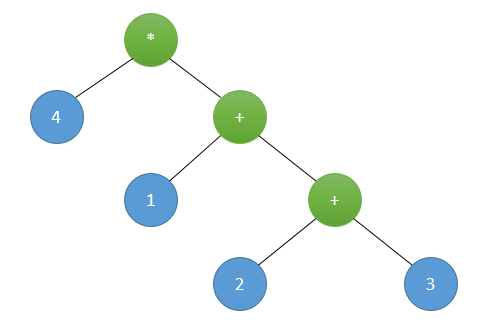
因此可以遍历所有二叉树可能的形式，4个数的全排列，从4种运算符中挑选3种运算符（运算符可以重复）

核心步骤1：需要遍历所有二叉树的可能，参考Eric Lippert的方法

class Node
{
    public Node Left { get; private set; }
    public Node Right { get; private set; }
    public Node(Node left, Node right)
    {
        this.Left = left;
        this.Right = right;
    }
}
 
static IEnumerable<Node> AllBinaryTrees(int size)
{
    if (size == )
        return new Node[] { null };
    return from i in Enumerable.Range(, size)
            from left in AllBinaryTrees(i)
            from right in AllBinaryTrees(size -  - i)
            select new Node(left, right);
}

核心步骤2：对于任意一个二叉树，构造表达式树

static Expression Build(Node node, List<double> numbers, List<Func<Expression, Expression, BinaryExpression>> operators)
{
    var iNum = ;
    var iOprt = ;
 
    Func<Node, Expression> f = null;
    f = n =>
    {
        Expression exp;
        if (n == null)
            exp = Expression.Constant(numbers[iNum++]);
        else
        {
            var left = f(n.Left);
            var right = f(n.Right);
            exp = operators[iOprt++](left, right);
        }
        return exp;
    };
    return f(node);
}

核心步骤3：遍历4个数字的全排列，全排列参考这里

static IEnumerable<List<T>> FullPermute<T>(List<T> elements)
{
    if (elements.Count == )
        return EnumerableOfOneElement(elements);
 
    IEnumerable<List<T>> result = null;
    foreach (T first in elements)
    {
        List<T> remaining = elements.ToArray().ToList();
        remaining.Remove(first);
        IEnumerable<List<T>> fullPermuteOfRemaining = FullPermute(remaining);
 
        foreach (List<T> permute in fullPermuteOfRemaining)
        {
            var arr = new List<T> { first };
            arr.AddRange(permute);
 
            var seq = EnumerableOfOneElement(arr);
            if (result == null)
                result = seq;
            else
                result = result.Union(seq);
        }
    }
    return result;
}
 
static IEnumerable<T> EnumerableOfOneElement<T>(T element)
{
    yield return element;
}

例如有四个数字{1, 2, 3, 4}，它的全排列如下：

, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , ,
, , , 

核心步骤4：从4种运算符中挑选3个运算符

static IEnumerable<IEnumerable<Func<Expression, Expression, BinaryExpression>>> OperatorPermute(List<Func<Expression, Expression, BinaryExpression>> operators)
{
    return from operator1 in operators
            from operator2 in operators
            from operator3 in operators
            select new[] { operator1, operator2, operator3 };
}

最后是Main函数：

static void Main(string[] args)
{
    List<double> numbers = new List<double> { , , ,  };
    var operators = new List<Func<Expression, Expression, BinaryExpression>> {
        Expression.Add,Expression.Subtract,Expression.Multiply,Expression.Divide
    };
 
    foreach (var operatorCombination in OperatorPermute(operators))
    {
        foreach (Node node in AllBinaryTrees())
        {
            foreach (List<double> permuteOfNumbers in FullPermute(numbers))
            {
                Expression expression = Build(node, permuteOfNumbers, operatorCombination.ToList());
                Func<double> compiled = Expression.Lambda<Func<double>>(expression).Compile();
                try
                {
                    var value = compiled();
                    if (Math.Abs(value - ) < 0.01)
                        Console.WriteLine("{0} = {1}", expression, value);
                }
                catch (DivideByZeroException) { }
            }
        }
    }
    Console.Read();
}

计算结果：

( * ( + ( + ))) =
( * ( + ( + ))) =
( * ( + ( + ))) =
( * ( + ( + ))) =
( * ( + ( + ))) =
( * ( + ( + ))) =
( * (( + ) + )) =
( * (( + ) + )) =
( * (( + ) + )) =
( * (( + ) + )) =
( * (( + ) + )) =
( * (( + ) + )) =
(( + ) * ( + )) =
(( + ) * ( + )) =
(( + ) * ( + )) =
(( + ) * ( + )) =
(( + ) * ( + )) =
(( + ) * ( + )) =
(( + ) * ( + )) =
(( + ) * ( + )) =
(( + ( + )) * ) =
(( + ( + )) * ) =
(( + ( + )) * ) =
(( + ( + )) * ) =
(( + ( + )) * ) =
(( + ( + )) * ) =
((( + ) + ) * ) =
((( + ) + ) * ) =
((( + ) + ) * ) =
((( + ) + ) * ) =
((( + ) + ) * ) =
((( + ) + ) * ) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * ( * ( * ))) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
( * (( * ) * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ) * ( * )) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
(( * ( * )) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
((( * ) * ) * ) =
(( * ( * )) / ) =
(( * ( * )) / ) =
(( * ( * )) / ) =
(( * ( * )) / ) =
(( * ( * )) / ) =
(( * ( * )) / ) =
((( * ) * ) / ) =
((( * ) * ) / ) =
((( * ) * ) / ) =
((( * ) * ) / ) =
((( * ) * ) / ) =
((( * ) * ) / ) =
( * (( * ) / )) =
( * (( * ) / )) =
( * (( * ) / )) =
( * (( * ) / )) =
( * (( * ) / )) =
( * (( * ) / )) =
(( * ) * ( / )) =
(( * ) * ( / )) =
(( * ) * ( / )) =
(( * ) * ( / )) =
(( * ) * ( / )) =
(( * ) * ( / )) =
((( * ) / ) * ) =
((( * ) / ) * ) =
((( * ) / ) * ) =
((( * ) / ) * ) =
((( * ) / ) * ) =
((( * ) / ) * ) =
( / ( / ( * ))) =
( / ( / ( * ))) =
( / ( / ( * ))) =
( / ( / ( * ))) =
( / ( / ( * ))) =
( / ( / ( * ))) =
(( * ) / ( / )) =
(( * ) / ( / )) =
(( * ) / ( / )) =
(( * ) / ( / )) =
(( * ) / ( / )) =
(( * ) / ( / )) =
( * ( * ( / ))) =
( * ( * ( / ))) =
( * ( * ( / ))) =
( * ( * ( / ))) =
( * ( * ( / ))) =
( * ( * ( / ))) =
( * (( / ) * )) =
( * (( / ) * )) =
( * (( / ) * )) =
( * (( / ) * )) =
( * (( / ) * )) =
( * (( / ) * )) =
(( / ) * ( * )) =
(( / ) * ( * )) =
(( / ) * ( * )) =
(( / ) * ( * )) =
(( / ) * ( * )) =
(( / ) * ( * )) =
(( * ( / )) * ) =
(( * ( / )) * ) =
(( * ( / )) * ) =
(( * ( / )) * ) =
(( * ( / )) * ) =
(( * ( / )) * ) =
((( / ) * ) * ) =
((( / ) * ) * ) =
((( / ) * ) * ) =
((( / ) * ) * ) =
((( / ) * ) * ) =
((( / ) * ) * ) =
( * ( / ( / ))) =
( * ( / ( / ))) =
( * ( / ( / ))) =
( * ( / ( / ))) =
( * ( / ( / ))) =
( * ( / ( / ))) =
(( / ( / )) * ) =
(( / ( / )) * ) =
(( / ( / )) * ) =
(( / ( / )) * ) =
(( / ( / )) * ) =
(( / ( / )) * ) =
( / (( / ) / )) =
( / (( / ) / )) =
( / (( / ) / )) =
( / (( / ) / )) =
( / (( / ) / )) =
( / (( / ) / )) = 

对于一些平时口算相对稍难的一些组合也是毫无压力，例如{1, 5, 5, 5}， {3, 3, 7, 7}， {3, 3, 8, 8}，有兴趣的看官口算试试 :)