Machine Learning in Action -- FP-growth

要解决的问题，频繁项集

最暴力的方法，就是遍历所有的项集组合，当然计算量过大
最典型的算法apriori, 算法核心思想，当一个集合不是频繁项集，那么它的超集也一定不是频繁项集
这个结论是很明显的，基于这样的思路，可以大大减少频繁项集的候选项
因为你只要发现一个集合非频繁项集，那么他所有的超集都可以忽略

但apriori算法的问题是，计算每个候选项的出现频率的时候都需要遍历整个数据集，这个明显是低效的
很自然的想法，就是否有办法可以尽量少的遍历数据集？比如遍历一遍就可以得到所有的项集的出现频率

那么这个就是FP-growth算法解决的问题

这个算法的典型应用，
比如在搜索引擎里面输入关键词时，后面会给出提示常用的词组合
这就需要效率很高的频繁项集挖掘算法

 

FP-tree

首先要构建FP-tree
只需要遍历数据集两遍，就可以完成FP-tree的构建，这个tree记录了所有频繁项集的出现频率

看例子，需要对如下数据集创建FP-tree

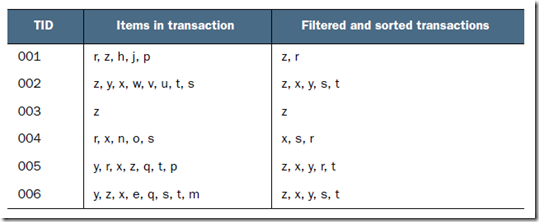
第一步，遍历数据集，计算所有元素项集的频率，即size=1的项，过滤掉非频繁项集，得到如下图的Header Table
并且对每条记录也进行过滤，过滤到非频繁的元素项，并使这条记录按照元素项的出现次数进行重新排序

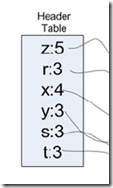
第一步其实是优化或预处理，减少需要计算的频繁项集的候选集
这里之所以需要排序，因为频繁项集关注的是组合而不是排列，而后面在生成树的时候需要避免生成重复的分支

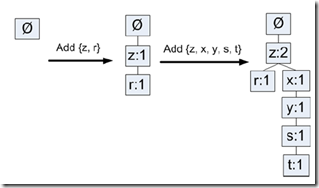
第二步，遍历数据集，构建FP-tree

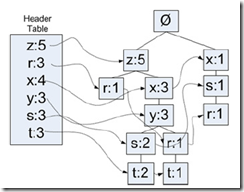
构建的过程很简单，看下图就明白了

代码实现

先定义FP-tree

class treeNode:
    def __init__(self, nameValue, numOccur, parentNode):
        self.name = nameValue #node name
        self.count = numOccur #出现频率
        self.nodeLink = None  #链接到相同节点
        self.parent = parentNode
        self.children = {}
    def inc(self, numOccur):
        self.count += numOccur
    def disp(self, ind=1): #用于打印树,debug用
        print ' '*ind, self.name, ' ', self.count
        for child in self.children.values():
            child.disp(ind+1)

载入数据，

def loadSimpDat():
    simpDat = [['r', 'z', 'h', 'j', 'p'],
                ['z', 'y', 'x', 'w', 'v', 'u', 't', 's'],
                ['z'],
                ['r', 'x', 'n', 'o', 's'],
                ['y', 'r', 'x', 'z', 'q', 't', 'p'],
                ['y', 'z', 'x', 'e', 'q', 's', 't', 'm']]
    return simpDat

def createInitSet(dataSet):
    retDict = {}
    for trans in dataSet:
        retDict[frozenset(trans)] = 1  #frozenset，即不可变set
    return retDict

得到的输入数据是这样的，看着比较怪，但后面递归的时候表示子串出现次数，不一定为1

>>> simpDat = fpGrowth.loadSimpDat()
>>> initSet = fpGrowth.createInitSet(simpDat)
>>> initSet
{frozenset(['e', 'm', 'q', 's', 't', 'y', 'x', 'z']): 1, frozenset(['x','s', 'r', 'o', 'n']): 1, frozenset(['s', 'u', 't', 'w', 'v', 'y', 'x',
'z']): 1, frozenset(['q', 'p', 'r', 't', 'y', 'x', 'z']): 1,frozenset(['h', 'r', 'z', 'p', 'j']): 1, frozenset(['z']): 1}

创建FP-tree的逻辑，

def createTree(dataSet, minSup=1): #minSup,最小的support(支持度),出现次数
    for trans in dataSet  #初始化heaerTable,计算所有item出现的次数
        for item in trans:
            headerTable[item] = headerTable.get(item, 0) + dataSet[trans]

    for k in headerTable.keys():
        if headerTable[k] < minSup: #删除非频繁项集
            del(headerTable[k])
    freqItemSet = set(headerTable.keys()) #得到频繁项集

    if len(freqItemSet) == 0: return None, None  #如果没有频繁项集,直接返回
    for k in headerTable:
        headerTable[k] = [headerTable[k], None]  #扩展headerTable,存储item的次数和第一个该item的引用,初始化时,引用为none

    retTree = treeNode('Null Set', 1, None)
    for tranSet, count in dataSet.items(): #每个tran
        localD = {}
        for item in tranSet: #每个item
            if item in freqItemSet: #过滤非频繁项集item
                localD[item] = headerTable[item][0] #localD存储该tran中的频繁item和该item在headerTable中的全局频率
        if len(localD) > 0:
            orderedItems = [v[0] for v in sorted(localD.items(), key=lambda p: p[1], reverse=True)] #按全局频率排序
            updateTree(orderedItems, retTree, headerTable, count) #用预处理过的orderedItems来更新树
    return retTree, headerTable

#递归算法,每次递归只处理第一个item
#并且items是排过序的,所以第一个item一定是root的children,第二个为第一个的children
def updateTree(items, inTree, headerTable, count):
    if items[0] in inTree.children: #看root的children中是否有items[0]
        inTree.children[items[0]].inc(count)  #有,增加count
    else:
        inTree.children[items[0]] = treeNode(items[0], count, inTree) #没有,为item[0]创建新的treenode
        if headerTable[items[0]][1] == None: #如果headerTable中该item的引用为空,直接指向item[0]
            headerTable[items[0]][1] = inTree.children[items[0]]
        else:  # 否则说明该item已经出现过,调用updateHeader
            updateHeader(headerTable[items[0]][1], inTree.children[items[0]])
    if len(items) > 1: #item[0]为root,继续update
        updateTree(items[1::], inTree.children[items[0]], headerTable, count)

#顺着headerTable的item引用,一直找到nodeLink为None, 即最后一次出现的item
#然后接上
def updateHeader(nodeToTest, targetNode):
    while (nodeToTest.nodeLink != None):
        nodeToTest = nodeToTest.nodeLink
    nodeToTest.nodeLink = targetNode

 

Mining frequent items from an FP-tree

发现频繁项集的过程和apriori一样，也是逐步递增的发现，即先找到size=1的，再去找size=2的。。。。。。

其实我们有了上面构建的FP-tree，就已经找到size=1的频繁集，即header table中所有的元素项

那现在的问题就是如何基于FP-tree找到size=2的频繁项集

 

conditional pattern bases

首先抽取条件模式基，

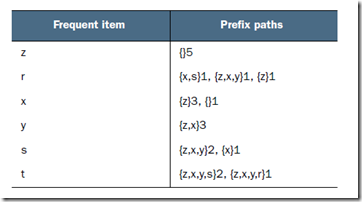
根据图，所谓条件模式基，是以每个频繁项集为结尾的，在FP-tree中所有可能的前缀路径

对应于前面的tansactioinSet

而由于前面在header table中存了每个频繁集所有出现的位置，通过链表可以很容易找到所有的条件模式基

比如，对于r，可以找到第一个r，z，第二个r，y，x，z。。。。。。

对于r，y，x，z，去掉r，然后按照全局频率排序得到z，x，y，后面的1表示r，z，x，y这个子串出现的次数

代码如下，

def ascendTree(leafNode, prefixPath): #递归找出某个树节点的前缀路径
    if leafNode.parent != None:
        prefixPath.append(leafNode.name)
        ascendTree(leafNode.parent, prefixPath)

def findPrefixPath(basePat, treeNode):
    condPats = {}
    while treeNode != None:
        prefixPath = []
        ascendTree(treeNode, prefixPath)
        if len(prefixPath) > 1:
            condPats[frozenset(prefixPath[1:])] = treeNode.count
        treeNode = treeNode.nodeLink #到下一个频繁项集出现的位置
    return condPats

>>> fpGrowth.findPrefixPath('x', myHeaderTab['x'][1])
{frozenset(['z']): 3}
>>> fpGrowth.findPrefixPath('z', myHeaderTab['z'][1])
{}
>>> fpGrowth.findPrefixPath('r', myHeaderTab['r'][1])
{frozenset(['x', 's']): 1, frozenset(['z']): 1,
frozenset(['y', 'x', 'z']): 1}

 

有了每个频繁项集的条件模式基，后面需求做的

对于每个频繁项集，基于他的条件模式基建立FP-tree，这样就可以找出size=2的频繁项集

直接看例子，需要创建t的FP-tree

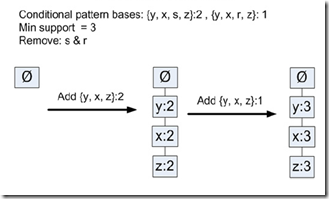
过程和前面建FP-tree是一样的，

先过滤非频繁项集，所以过滤掉r，s，因为在条件模式基中，s出现s×2次，而r出现r×1次

再创建FP-tree，得到频繁项集为，y，x，z

于是我们就找到size=2的频繁项集，

t，y；t，x；t，z

下面要找到size=3的频繁项集只需要重复上面的过程，找到size=2频繁项集的条件模式基，在各自构建FP-tree

代码，

#inTree，FP-tree
#preFix，前缀，上面例子中的t
#freqItemList，保存所有的频繁项集
def mineTree(inTree, headerTable, minSup, preFix, freqItemList):
    #返回headerTable中的所有的item名(v[0]),并以全局频率排序
    bigL = [v[0] for v in sorted(headerTable.items(),key=lambda p: p[1])]
    for basePat in bigL: #上面例子，y,x,z
        newFreqSet = preFix.copy() #先将前缀拷过来，上面例子't'
        newFreqSet.add(basePat) #拼成新的频繁集，如t,y
        freqItemList.append(newFreqSet) #将频繁集加入freqItemList
        condPattBases = findPrefixPath(basePat, headerTable[basePat][1]) #生成条件模式基，比如生成t,y的
         myCondTree, myHead = createTree(condPattBases,minSup) #构造FP-tree
        if myHead != None:
            mineTree(myCondTree, myHead, minSup, newFreqSet, freqItemList) #递归调用