codeforces 577E E. Points on Plane(构造+分块)

题目链接：

E. Points on Plane

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

On a plane are n points (xi, yi) with integer coordinates between 0 and 106. The distance between the two points with numbers a and bis said to be the following value: 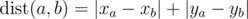 (the distance calculated by such formula is called Manhattan distance).

We call a hamiltonian path to be some permutation pi of numbers from 1 to n. We say that the length of this path is value .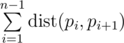

Find some hamiltonian path with a length of no more than 25 × 108. Note that you do not have to minimize the path length.

Input

The first line contains integer n (1 ≤ n ≤ 106).

The i + 1-th line contains the coordinates of the i-th point: xi and yi (0 ≤ xi, yi ≤ 106).

It is guaranteed that no two points coincide.

Output

Print the permutation of numbers pi from 1 to n — the sought Hamiltonian path. The permutation must meet the inequality .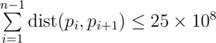

If there are multiple possible answers, print any of them.

It is guaranteed that the answer exists.

Examples

input

5
0 7
8 10
3 4
5 0
9 12

output

4 3 1 2 5 
 
题意：
 
现在给n个点,要求你找到一个顺序,这个顺序中的曼哈顿距离不能超过25*1e8;
 
思路：
 
构造的题,想到原来莫队算法中给数分块,然后降低复杂度的思想,然后我就想分块,然后看一下在最坏的情况下是否会超过上限;
按1e3的长度分块,然后这个块内要么按y的升序要么按Y的降序排列,这样每个块内平均下来最大的距离是1e3*1e3+1e6=2e6,一共1e3个块,所以一共2e9的距离符合要求;
还有就是要按块的位置升降序交替,使点呈现v和倒v的状态,不然每两个块相靠的地方会多出一个1e6,最后多了1e9就过不了了;
 
AC代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <bits/stdc++.h>
#include <stack>
#include <map>
 
using namespace std;
 
#define For(i,j,n) for(int i=j;i<=n;i++)
#define mst(ss,b) memset(ss,b,sizeof(ss));
 
typedef  long long LL;
 
template<class T> void read(T&num) {
    char CH; bool F=false;
    for(CH=getchar();CH<'0'||CH>'9';F= CH=='-',CH=getchar());
    for(num=0;CH>='0'&&CH<='9';num=num*10+CH-'0',CH=getchar());
    F && (num=-num);
}
int stk[70], tp;
template<class T> inline void print(T p) {
    if(!p) { puts("0"); return; }
    while(p) stk[++ tp] = p%10, p/=10;
    while(tp) putchar(stk[tp--] + '0');
    putchar('\n');
}
 
const int mod=1e9+7;
const double PI=acos(-1.0);
const int inf=1e9;
const int N=1e6+20;
const int maxn=1e3;
const double eps=1e-12;
 
struct node
{
    int x,y,id,pos;
}po[N];
int n;
int cmp(node a,node b)
{
    if(a.pos==b.pos)
    {
        if(a.pos%2==1)return a.y<b.y;
        return a.y>b.y;
    }
    return a.pos<b.pos;
}
int main()
{
    read(n);
    For(i,1,n)
    {
        read(po[i].x);
        read(po[i].y);
        po[i].pos=po[i].x/maxn;
        po[i].id=i;
    }
    sort(po+1,po+n+1,cmp);
    For(i,1,n)printf("%d ",po[i].id);
    return 0;
}