[NOIP2011] 提高组 洛谷P1314 聪明的质监员

题目描述

小T 是一名质量监督员，最近负责检验一批矿产的质量。这批矿产共有 n 个矿石，从 1到n 逐一编号，每个矿石都有自己的重量 wi 以及价值vi 。检验矿产的流程是：

1 、给定m 个区间[Li,Ri]；

2 、选出一个参数 W；

3 、对于一个区间[Li,Ri]，计算矿石在这个区间上的检验值Yi：

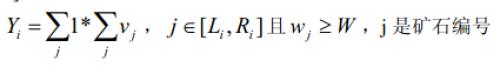
这批矿产的检验结果Y 为各个区间的检验值之和。即：Y1+Y2...+Ym

若这批矿产的检验结果与所给标准值S 相差太多，就需要再去检验另一批矿产。小T

不想费时间去检验另一批矿产，所以他想通过调整参数W 的值，让检验结果尽可能的靠近

标准值S，即使得S-Y 的绝对值最小。请你帮忙求出这个最小值。

输入输出格式

输入格式：

输入文件qc.in 。

第一行包含三个整数n，m，S，分别表示矿石的个数、区间的个数和标准值。

接下来的n 行，每行2个整数，中间用空格隔开，第i+1 行表示 i 号矿石的重量 wi 和价值vi。

接下来的m 行，表示区间，每行2 个整数，中间用空格隔开，第i+n+1 行表示区间[Li,Ri]的两个端点Li 和Ri。注意：不同区间可能重合或相互重叠。

输出格式：

输出文件名为qc.out。

输出只有一行，包含一个整数，表示所求的最小值。

输入输出样例

输入样例#1：

5 3 15
1 5
2 5
3 5
4 5
5 5
1 5
2 4
3 3 

输出样例#1：

10

说明

【输入输出样例说明】

当W 选4 的时候，三个区间上检验值分别为 20、5 、0 ，这批矿产的检验结果为 25，此

时与标准值S 相差最小为10。

【数据范围】

对于10% 的数据，有 1 ≤n ，m≤10；

对于30% 的数据，有 1 ≤n ，m≤500 ；

对于50% 的数据，有 1 ≤n ，m≤5,000；

对于70% 的数据，有 1 ≤n ，m≤10,000 ；

对于100%的数据，有 1 ≤n ，m≤200,000，0 < wi, vi≤10^6，0 < S≤10^12，1 ≤Li ≤Ri ≤n 。

二分参数w，按照题中公式求最小答案。

利用前缀和加速运算。

 #include<cstdio>
 #include<iostream>
 #include<algorithm>
 #include<cmath>
 using namespace std;
 int n,m;
 long long mx,s;
 long long ans=;
 struct st{
     int a;
     int b;
 }a[],rg[];//a-矿石 rg-范围
 long long sv[],sc[];//从1到[i]范围内：价值大于w的矿石的价值和，个数和
 long long su(int w){
     int i,j;
 //    sv[0]=0;
 //    sc[0]=0;
     for(i=;i<=n;i++){
         sv[i]=sv[i-];
         sc[i]=sc[i-];
         if(a[i].a>=w){sv[i]+=a[i].b;sc[i]++;}
     }
     long long sm=;
     for(i=;i<=m;i++){
         sm+=(sv[rg[i].b]-sv[rg[i].a])*(sc[rg[i].b]-sc[rg[i].a]);
     }
     return sm;
 }
 int main(){
     scanf("%d%d%lld",&n,&m,&s);
     int i,j;
     for(i=;i<=n;i++){
         scanf("%d%d",&a[i].a,&a[i].b);
         if(a[i].b>mx)mx=a[i].b;
     }
     for(i=;i<=m;i++)
         scanf("%d%d",&rg[i].a,&rg[i].b),rg[i].a--;
     long long mi=,mid,res;
     while(mi<=mx){
         mid=(mi+mx)/;
         res=su(mid);
         if(res==s){printf("");return ;}
         if(abs(res-s)<ans)ans=abs(res-s);
         if(res>s)mi=mid+;
         else mx=mid-;
     }
     printf("%lld",ans);
     return ;
 }