[NOIP2008] 提高组 洛谷P1155 双栈排序

题目描述

Tom最近在研究一个有趣的排序问题。如图所示，通过2个栈S1和S2，Tom希望借助以下4种操作实现将输入序列升序排序。

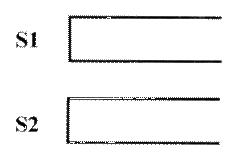
操作a

如果输入序列不为空，将第一个元素压入栈S1

操作b

如果栈S1不为空，将S1栈顶元素弹出至输出序列

操作c

如果输入序列不为空，将第一个元素压入栈S2

操作d

如果栈S2不为空，将S2栈顶元素弹出至输出序列

如果一个1~n的排列P可以通过一系列操作使得输出序列为1，2，…，(n-1)，n，Tom就称P是一个“可双栈排序排列”。例如(1,3,2,4)就是一个“可双栈排序序列”，而(2,3,4,1)不是。下图描述了一个将(1,3,2,4)排序的操作序列：<a,c,c,b,a,d,d,b>

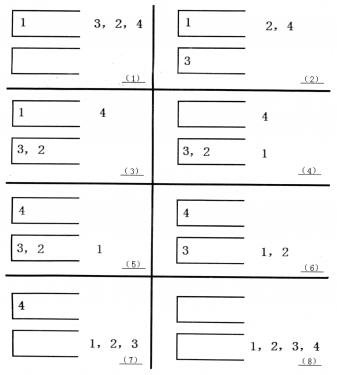
当然，这样的操作序列有可能有几个，对于上例(1,3,2,4)，<a,c,c,b,a,d,d,b>是另外一个可行的操作序列。Tom希望知道其中字典序最小的操作序列是什么。

输入输出格式

输入格式：

输入文件twostack.in的第一行是一个整数n。

第二行有n个用空格隔开的正整数，构成一个1~n的排列。

输出格式：

输出文件twostack.out共一行，如果输入的排列不是“可双栈排序排列”，输出数字0；否则输出字典序最小的操作序列，每两个操作之间用空格隔开，行尾没有空格。

输入输出样例

输入样例#1：

【输入样例1】
4
1 3 2 4
【输入样例2】
4
2 3 4 1
【输入样例3】
3
2 3 1

输出样例#1：

【输出样例1】
a b a a b b a b
【输出样例2】
0
【输出样例3】
a c a b b d

说明

30%的数据满足： n<=10

50%的数据满足： n<=50

100%的数据满足： n<=1000

考虑单栈排序：如果有三个元素a[i]<a[j] && a[i]>a[k]，且它们的顺序 i<j<k，a[i]出栈以后a[j]才能进栈，a[k]出栈以后a[i]才能出栈，显然无法满足要求。

所以，如果三个数满足以上条件，它们是不能同进一个栈的。

先n downto 1倒推出每个数后面最小的数，作为a[k],然后枚举a[i],a[j],若符合上述条件，则在i，j之间连边，表示它们不能进同一个栈。

之后进行二分图染色，如果遇到颜色矛盾，说明不能把冲突的点对分成两组，也就是问题无解。

如果没有冲突，则问题有解，模拟即可。

 /*by SilverN*/
 #include<iostream>
 #include<algorithm>
 #include<cstring>
 #include<cstdio>
 #include<cmath>
 #include<stack>
 using namespace std;
 const int mxn=;
 struct edge{
     int v;
     int nxt;
 }e[mxn];
 int hd[mxn],mct=;
 void add_edge(int u,int v){
     e[++mct].v=v;e[mct].nxt=hd[u];hd[u]=mct;
     return;
 }
 int a[mxn],n;
 int mini[mxn];
 int c[mxn];
 int ans[mxn],t=;
 bool dfs(int u){
     if(c[u]==-)c[u]=;
     for(int i=hd[u];i;i=e[i].nxt){
         int v=e[i].v;
         if(c[v]==-){
             c[v]=c[u]^;
             if(!dfs(v))return ;
         }
         else{
             if(c[v]==c[u])return ;
         }
     }
     return ;
 }
 stack<int>tp1,tp2;
 int main(){
     memset(c,-,sizeof c);
     int i,j;
     scanf("%d",&n);
     mini[n+]=0x3f3f3f;
     for(i=;i<=n;i++)scanf("%d",&a[i]);
     for(i=n;i;i--) mini[i]=min(mini[i+],a[i]);
     for(i=;i<n;i++)
      for(j=i+;j<=n;j++){
          if(a[i]<a[j] && a[i]>mini[j+]){
              add_edge(j,i);
              add_edge(i,j);
          }
      }
     for(i=;i<=n;i++)
         if(c[i]==-){
             if(!dfs(i)){
                 printf("0\n");
                 return ;
             }
         }
     int now=;
     i=;
     while(){
         if(now>n)break;
         if(c[i]== && (tp1.empty() || tp1.top()>a[i])){
             tp1.push(a[i]);
             ans[++t]=;
             i++;
             continue;
         }
         if(!tp1.empty() && tp1.top()==now){
             ans[++t]=;
             tp1.pop();
             now++;
             continue;
         }
         if(c[i]== && (tp2.empty() || tp2.top()>a[i])){
             tp2.push(a[i]);
             ans[++t]=;
             i++;
             continue;
         }
         if(!tp2.empty() && tp2.top()==now){
             tp2.pop();
             ans[++t]=;
             now++;
             continue;
         }
     }
     for(i=;i<=t;i++)printf("%c ",(char)ans[i]+'a'-);
     printf("\n");
     return ;
 }