luogu P1516 青蛙的约会(线性同余方程扩展欧几里德）

题意

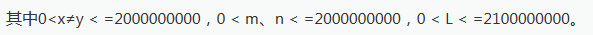
题解

做了这道题，发现扩欧快忘了。

根据题意可以很快地列出线性同余方程。

设跳了k次

x+mkΞy+nk(mod l)

(m-n)kΞ-(x-y)(mod l)

然后化一下

(m-n)k+(x-y)Ξ0(mod l)

也就是前面一坨是l的倍数

不妨设

(m-n)k+(x-y)=-tl

(m-n)k+tl=-(x-y)

我们要求的就是保证t<=0(因为我们设的-t倍的l，所以t<=0),k>=0时k的最小值

发现这是一个不定方程

根据裴蜀定理（这个定理搜狗输入法上没有）

当-(x-y)是gcd((m-n),t)的倍数时是有解的。（等式两边都乘-(x-y)/gcd就行了）且(m-n)k+tl=gcd((m-n),t)一定有整数解

所以我们用扩欧算出(m-n)k+tl=gcd((m-n),t)的一组特解和gcd

然后通过判断-(x-y)是不是gcd((m-n),t)的倍数判断有没有解。

假如有解我们就先保证（m-n）为正数根据k的通解公式k=-(x-y)/gcd*k0+h*l/gcd(h为整数）

然后求出最小的正数k就行了

然后这样做似乎没有保证t<=0

其实保证了

考虑通项公式。其实那个k0的系数-(x-y)/gcd

是因为我们要把(m-n)k+tl=gcd((m-n),t)化为-(x-y)/gcd(m-n)k+-(x-y)/gcdtl=-(x-y)给等式两边乘的

这样保证现在-(x-y)/gcd(m-n)k是大于等于-(x-y)的（当-(x-y)为正数）这样t<=0没什么问题。

当当-(x-y)为负数时我们发现-(x-y)/gcd(m-n)k小于等于-(x-y)此时t也变号了所以要求t>=0也没问题。

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 long long x,y,n,m,l,xx,yy;
 long long exgcd(long long a,long long b,long long &x,long long &y){
     if(b==){
         x=;
         return a;
     }
     long long c=exgcd(b,a%b,x,y);
     long long z=x;
     x=y;y=z-(a/b)*y;
     return c;
 }
 int main(){
     scanf("%lld%lld%lld%lld%lld",&x,&y,&m,&n,&l);
     long long a=m-n;long long b=y-x;
     if(a<){
         a=-a;
         b=-b;
     }
     long long gcd=exgcd(a,l,xx,yy);
     if(b%gcd!=){
         printf("Impossible");
     }
     else printf("%lld",(xx*(b/gcd)%(l/gcd)+(l/gcd))%(l/gcd));
     return ;
 }