hdu3360National Treasures (最大匹配，拆点法)

National Treasures

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)

Total Submission(s): 1038 Accepted Submission(s): 364

Problem Description

The great hall of the national museum has been robbed few times recently. Everyone is now worried about the security of the treasures on display. To help secure the hall, the museum contracted with a private security company to provide
additional guards to stay in the great hall and keep an eye on the ancient artifacts. The museum would like to hire the minimum number of additional guards so that the great hall is secured.

The great hall is represented as a two dimensional grid of R × C cells. Some cells are already occupied with the museum’s guards. All remaining cells are occupied by artifacts of different types (statues, sculptures, . . . etc.) which can be replaced by new
hired guards. For each artifact, few other cells in the hall are identified as critical points of the artifact depending on the artifact value, type of vault it is kept inside, and few other factors. In other words, if this artifact is going to stay in the
hall then all of its critical points must have guards standing on them. A guard standing in a critical position of multiple artifacts can keep an eye on them all. A guard, however,

can not stand in a cell which contains an artifact (instead, you may remove the artifact to allow the guard to stay there). Also you can not remove an artifact and leave the space free (you can only replace an artifact with a new hired guard).

Surveying all the artifacts in the great hall you figured out that the critical points of any artifact (marked by a ) are always a subset of the 12 neighboring cells as shown in the grid below.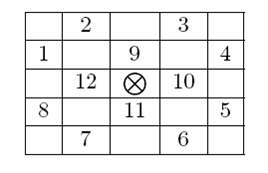








Accordingly, the type of an artifact can be specified as a non-negative integer where the i-th bit is 1 only if critical point number i from the picture above is a critical point of that artifact. For example an artifact of type 595 (in binary 1001010011) can
be pictured as shown in the figure below. Note that bits are numbered from right to left (the right-most bit is bit number 1.) If a critical point of an artifact lies outside the hall grid then it is considered secure.








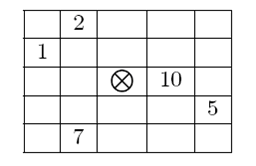
You are given the layout of the great hall and are asked to find the minimum number of additional guards to hire such that all remaining artifacts are secured.

Input

Your program will be tested on one or more test cases. Each test case is specified using R+1 lines.

The first line specifies two integers (1<= R,C <= 50) which are the dimensions of the museum hall. The next R lines contain C integers separated by one or more spaces. The j-th integer of the i-th row is -1 if cell (i, j) already contains one of the museum’s
guards, otherwise it contains an integer (0 <= T <= 2¹²) representing the type of the artifact in that cell.

The last line of the input file has two zeros.

Output

For each test case, print the following line:

k. G

Where k is the test case number (starting at one,) and G is the minimum number of additional guards to hire such that all remaining artifacts are secured.

Sample Input

1 3
512 -1 2048
2 3
512 2560 2048
512 2560 2048
0 0

Sample Output

1. 0
2. 2

Hint

The picture below shows the solution of the second test case where the  two artifacts in the middle are replaced by guards.

Source

2009 ANARC

这题看似与方向有关，当前位置仅仅与它保护的位置是单向的，但并不是是这种，我们来分析一下。

从当前题意可知，保护位置与被保护位置是奇偶对立的，所以我们能够先把点分成奇偶两部分，每一部分内部是不会有关连的，且每一个点是独一无二的，如果是有向的，保护点指向被保护点，建图，左偶右奇，那么如今是要求最小顶点覆盖，先从左指向右求起，求完之后，如果左边没有匹配的点是被保护点，之后再求右指向左的匹配，但右边部分点己经有匹配的点就不用匹配了，那么也就是求右边未匹配的点和左边未匹配的点匹配，这样匹配是一对一的，所以这种匹配也可觉得是求左边未匹配的点与右边未匹配的点相匹配。----------综上得知，这是一个无向区配。

是一个无向的话就有两种求法：

一种是：把图分成奇偶两部分，求最小顶点覆盖。        还有一种是：求最大匹配。

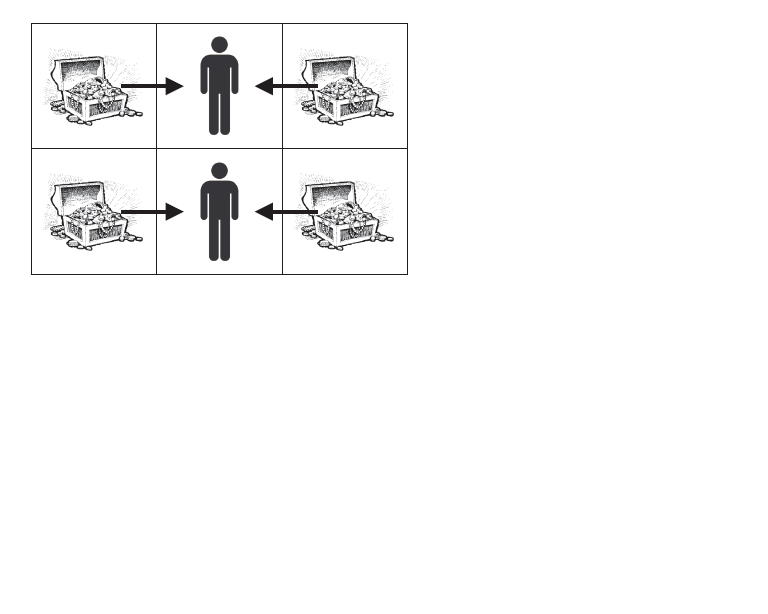
#include<stdio.h>
#include<vector>
#include<iostream>
using namespace std;
int match[2505],vist[2505];
vector<int>map[2505];
int find(int i)
{
    for(int j=0;j<map[i].size();j++)
    if(!vist[map[i][j]])
    {
        vist[map[i][j]]=1;
        if(match[map[i][j]]==-1||find(match[map[i][j]]))
        {
            match[map[i][j]]=i; return 1;
        }
    }
    return 0;
}
int main()
{
    int dir[12][2]={-1,-2,-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,0,0,1,1,0,0,-1};
    int n,m,mp[55][55],b_w[55][55],bn,wn,k=0;
    while(scanf("%d%d",&n,&m)>0&&n+m!=0)
    {
        for(int i=0;i<n*m;i++)
        {
            map[i].clear(),match[i]=-1;
        }

        for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        scanf("%d",&mp[i][j]);
        for(int i=0;i<n;i++)
        for(int j=0;j<m;j++)
        if(mp[i][j]!=-1)
        {
            int ti,tj;
            for(int e=0;e<12;e++)
            if(mp[i][j]&(1<<e))
            {
                ti=i+dir[e][0]; tj=j+dir[e][1];
                if(ti>=0&&ti<n&&tj>=0&&tj<m&&mp[ti][tj]!=-1)
                {
                    map[ti*m+tj].push_back(i*m+j);
                    map[i*m+j].push_back(ti*m+tj);
                }
            }
        }
        int ans=0;
        for(int i=0;i<n*m;i++)
        {
            for(int j=0;j<n*m;j++)
            vist[j]=0;
            ans+=find(i);
        }
        printf("%d. %d\n",++k,ans/2);
    }
}