Gartner 魔力象限介绍

Gartner(高德纳)全球最具权威的IT市场研究与顾问咨询公司，他总是不停地推出IT行业的各种报告以及著名的Gartner魔力象限。

Gartner魔力象限通常从两个方面来评价供应商： 前瞻性（Completeness of Vision）和执行能力（Ability to Execute）。涵盖的公司包括：Leaders领导者、challengers挑战者、Visionaries有远见者、Niche Players特定领域者。

前者考量该厂商提供产品底层技术基础的能力、市场领导能力、创新能力、外部投资等， 后者考量产品的易用程度和价格、服务的完善程度和技 术支持能力、管理团队的经验和能力等。 象限图的横轴表示发前瞻性，纵轴表示执行能力。

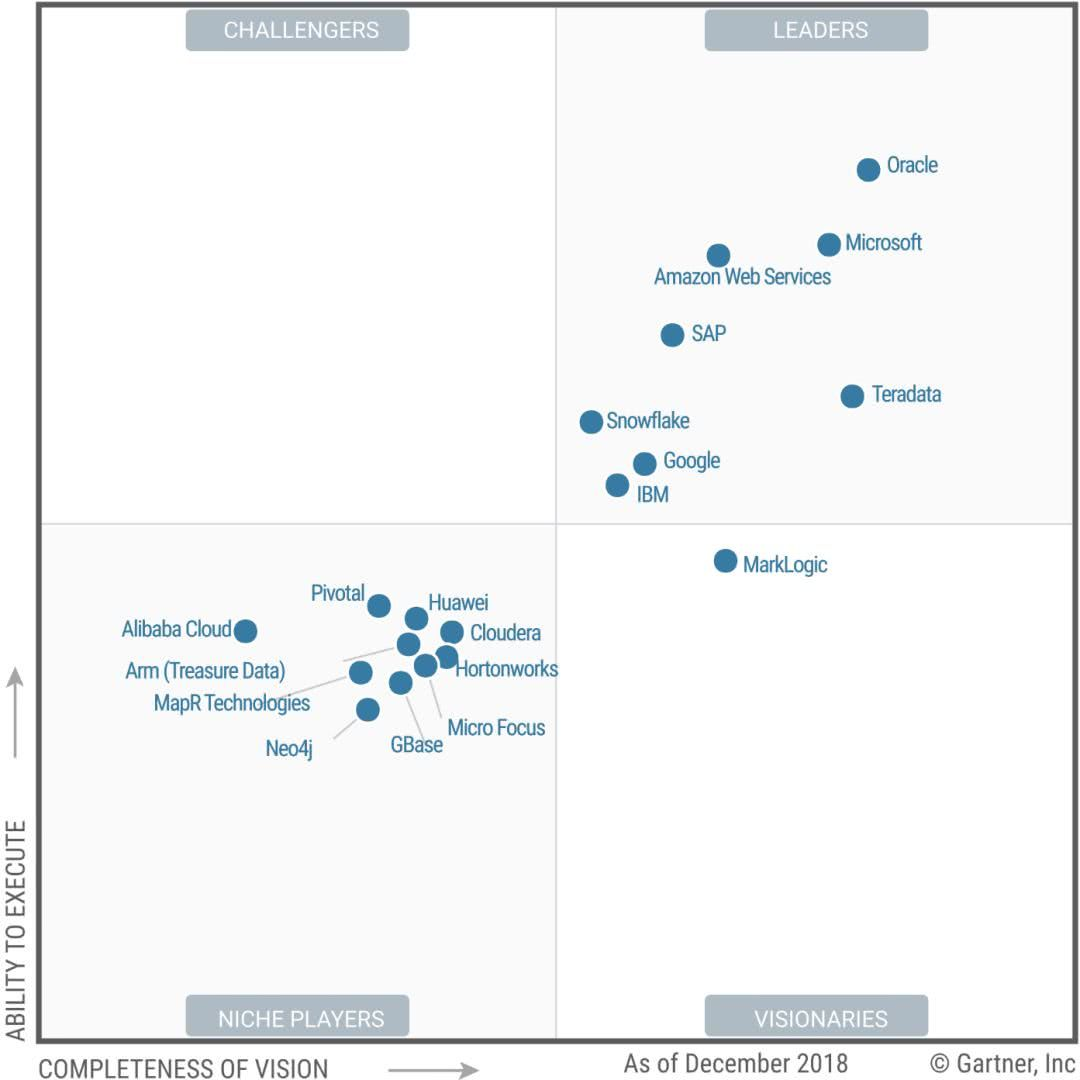
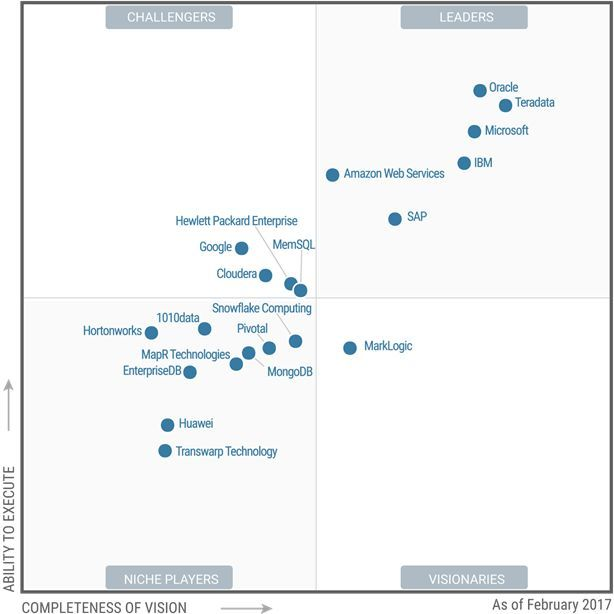
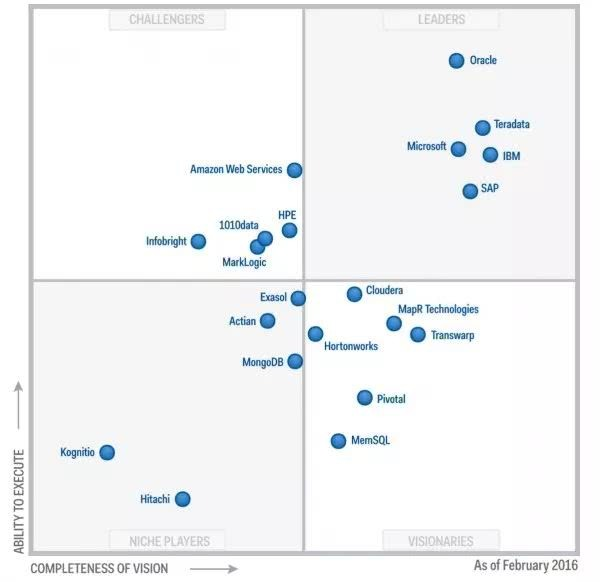
Gartner 2019-2018-2017-2016年分析型数据管理解决方案（DMSA）魔力象限

面向分析的数据管理解决方案（DMSA）被定义为“支持和管理一个或多个文件管理系统（通常是数据库）中数据的完整软件系统。这类解决方案的四大使用场合，包括传统数据仓库、实时数据仓库、与上下文无关的数据仓库以及逻辑数据仓库。

 

Gartner 2019年数据科学和机器学习平台魔力象限（截至2018年11月）

  

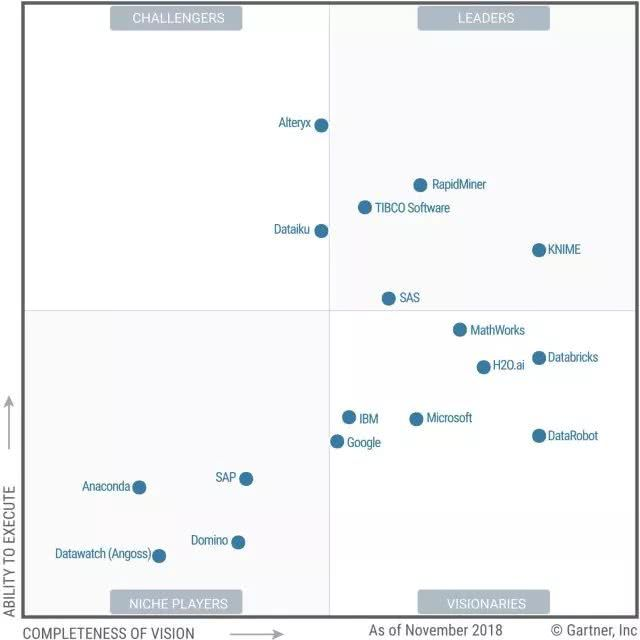
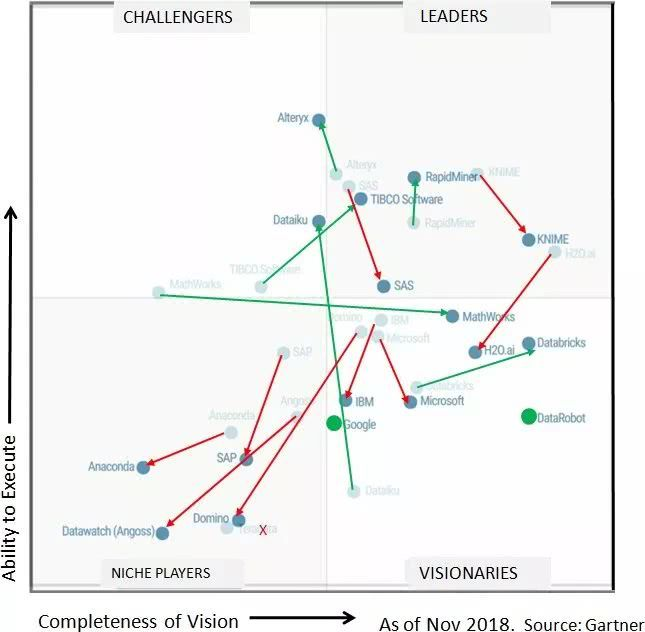
Gartner数据科学和机器学习平台魔力象限，2019年与2018年比较。2018年魔力象限（灰色背景图）和2019年魔力象限（前景图）的结果，箭头连接代表同一家公司的圆圈。如果公司位置大幅改善（远离原位置），箭头标以绿色，如果公司位置下降，箭头标以红色。绿色圆圈表示2家新公司（谷歌和DataRobot），红色X标志着今年跌出象限的供应商（Teradata）。

参考文章：

Gartner：2019年“数据管理解决方案”魔力象限

Gartner 2019年AI 平台魔力象限

Teradata在大数据管理与分析领域连续18年评测排名第一的更多相关文章

  1. 物联网、5G世界与大数据管理

    物联网带动中国产业转型.推动社会经济发展的时代已经到来.什么是物联网?物联网又给数据管理带来了哪些挑战?面对挑战,我们有怎样的解决方案?本文中我们将一一为您揭晓.     01 物联网时代的到来   ...

  2. 深入解析DC/OS 1.8 – 高可靠的微服务及大数据管理平台

    深入解析DC/OS 1.8 – 高可靠的微服务及大数据管理平台 大家好,欢迎大家参加这次DC/OS的技术分享. 先做个自我介绍,刘超,Linker Networks首席架构师,Open DC/OS社区 ...

  3. 南大《软件分析》课程笔记——Intermediate Representation

    南大<软件分析>--Intermediate Representation @(静态分析) Content 编译器和静态分析的关系 AST vs IR IR:3-地址代码(3AC) 实际静 ...

  4. 大作业NABC分析结果

    大作业NABC分析结果 这次的大作业计划制作一款关于七巧板的游戏软件.关于编写的APP的NABC需求分析: N:需求 ,本款软件主要面向一些在校的大学生,他们在校空闲时间比较多,而且热衷于一些益智类游 ...

  5. 阿里云资深DBA专家罗龙九:云数据库十大经典案例分析【转载】

    阿里云资深DBA专家罗龙九:云数据库十大经典案例分析 2016-07-21 06:33 本文已获阿里云授权发布,转载具体要求见文末 摘要:本文根据阿里云资深DBA专家罗龙九在首届阿里巴巴在线峰会的&l ...

  6. 在HDInsight中从Hadoop的兼容BLOB存储查询大数据的分析

    在HDInsight中从Hadoop的兼容BLOB存储查询大数据的分析 低成本的Blob存储是一个强大的.通用的Hadoop兼容Azure存储解决方式无缝集成HDInsight.通过Hadoop分布式 ...

  7. 统计_statistics_不同的人_大样本_分析_统计方法_useful ？

    统计_statistics_不同的人_大样本_分析_

  8. 南大《软件分析》课程笔记——Data Flow Analysis

    南大<软件分析>--Data Flow Analysis @(静态分析) 目录 数据流分析概述 数据流分析应用 Reaching Definitions Analysis(may anal ...

  9. 第二篇：智能电网(Smart Grid)中的数据工程与大数据案例分析

    前言 上篇文章中讲到,在智能电网的控制与管理侧中,数据的分析和挖掘.可视化等工作属于核心环节.除此之外,二次侧中需要对数据进行采集,数据共享平台的搭建显然也涉及到数据的管理.那么在智能电网领域中,数据 ...

随机推荐

  1. 字体大小之px、em、rem、pt,字号详解

    PX px像素(Pixel).相对长度单位.像素px是相对于显示器屏幕分辨率而言的. 是一个虚拟长度单位,是计算机系统的数字化图像长度单位,如果px要换算成物理长度,需要指定精度DPI(Dots Pe ...

  2. Visible Trees

    Visible Trees Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others) Pr ...

  3. 0209利用innobackupex进行简单数据库的备份

    利用innobackupex进行简单数据库的备份yum install perl-DBIyum install perl-DBD-MySQLyum install perl-Time-HiResyum ...

  4. hdu 1239

    首先,p,q>=2,所以p,q<=50000; 然后,我们观察a<=b<1000,而p,q<=100000.那么,q>=10000时,p<=10,则a/b&l ...

  5. ABCDE

    ABCDE A-Artificial intelligence 人工智能 B-Block chain 区块链 C-Cloud 云 D-Big Data 大数据 E-Ecology 互联网生态是以互联网 ...

  6. 【STL容器学习】-关联容器与map的用法

    STL提供了4个关联容器:set.multiset.map和multimap.这些容器提供了通过keyword高速存储和訪问数据元素的能力.Set和map不同意有反复keyword,而multiset ...

  7. iOS不同版本号适配问题(#ifdef __IPHONE_7_0)

    部分參考http://www.cnblogs.com/ios8/p/ios-version-com.html 以下举个简单的样例来说明在iOS7.0和iOS6.1(以及更低版本号)之间的适配问题(用的 ...

  8. mysql选择上一条、下一条数据记录，排序上移、下移、置顶

    1.功能须要 完毕列表排序上移,下移,置顶功能.效果例如以下图所看到的: 2设置思路 设置一个rank为之间戳,通过选择上移,就是将本记录与上一条记录rank值交换,下移就是将本条记录与下一条记录ra ...

  9. 创建MFC应用程序的类型：单文档+多文档+基于对话框

    单文档支持文档视图架构.数据的保存--(读取--改动)文档类功能--显示(视图类功能),比較方便. 基于对话框,主窗体是对话框类型.能够方便的使用控件,所见即所得的编程,比較方便. 单文档类似&quo ...

  10. spring属性的三种注入方法

    (1)使用set方法: public class Book {  private String bookname;public void setBookname(String bookname) {  ...