PAC学习理论:机器学习那些事
参考翻译,有大量删除和修改,如有异议,请拜访原文。一定要看英文原文!!!。
本文转载于:深度译文:机器学习那些事
英文【原题】A Few Useful Things to Know About Machine Learning
机器学习是有别于专家系统(基于知识/规则)的一种模式识别方法,与专家系统的构建方法不同,但目的相同。本文分析了一众机器学习方法,并给出了一些机器学习概念的通俗解释。
通俗论述的理论解释在第二段,由公式详细说明。
参考链接:PAC可学习
一、机器学习那点事
学习=表示 + 评价+ 优化
假设有一个应用,你认为机器学习有可能在其中发挥作用。那么,你面临的第一个问题是各种机器学习算法令人眼花缭乱。应挑选使用哪一个?现在有成千上万的机器学习算法,每年还有成百上千的新算法发表出来。免迷失在这么多算法中的关键是,要认识到这些算法都是由三个部分组成的,分别是:
表示(Representation)
一个分类器必须用计算机可以处理的某种形式语言来表示。反过来讲,为学习器选择一种表示,就意味选择一个特定的分类器集合。学习器可能学出的分类器只能在这个集合中。这个集合被称为学习器的假设空间(hypothesis space)。如果某个分类器不在该空间中,它就不可能被该学习器学到。与此相关的一个问题是如何表示输入,即使用哪些特征,本文稍后介绍。
评价(Evaluation)
我们需要一个评价函数(亦称为目标函数或打分函数)来判断分类器的优劣。机器学习算法内部使用的评价函数和我们希望分类器进行优化的外部评价函数有所不同。这是为了便于优化,接下来会讨论。
优化(Optimization)
最后,我们需要一个搜索方法,能够在假设空间中找到评价函数得分最高的那个分类器。
一些学习机制的优化方法
使用什么样的模型表示什么样的假设,使用怎样的评价方法,使用什么样的优化方法筛选最优假设。
下面的图有问题,有误导性,应该上原图!!!!:

..................
..................
当然,并不是表 1 中从各列选出元素的相互组合都同样有意义。例如,离散表示很自然地与组合优化相结合;而连续表示则与连续优化相结合。然而,很多学习器同时包含离散和连续的部分。实际上,所有可能的组合也都快被实现过了。
过拟合(Overfitting)有多张面孔
如果我们拥有的知识和数据并不足以学习出正确的分类器,将会怎样呢?我们就得冒风险构建一个分类器(或者其中一部分),这个分类器并非建立在现实基础上,而是将数据随机表现加以解读。这个问题称为过拟合,它是机器学习中的棘手问题。当你的学习器输出的分类器在训练数据上准确率为 100%,而在测试数据上仅有 50% 的时候(而本来可以学到一个分类器能够在两个数据上均达到 75% 的准确率),说明这个分类器发生过拟合了。
机器学习领域的每个人都了解过拟合,但过拟合会以多种并不明显的形式出现。一种理解过拟合的方式是将泛化误差(generalization error)分解为偏置(bias)和方差( variance)【9】。偏置度量了学习器倾向于一直学习相同错误的程度。方差则度量了学习器倾向于忽略真实信号、学习随机事物的程度。图 1用朝板子扔飞镖作为类比进行了直观说明。

一个线性学习器有较高的偏置,因为当两个类别的交界不是超平面的时候,这个学习器就无法进行归纳(摘注:原文 A linear learner has high bias, because when the frontier between two classes is not a hyper-plane the learner is unable
to induce it)。决策树就不会有这个问题,因为它可以表示任意的布尔函数,但在另一方面,决策树会面临高方差的问题:在同一现象所产生的不同训练数据上学习的决策树往往差异巨大,而实际上它们应当是相同的。类似道理也适用于优化方法的选择上:与贪心搜索相比,柱搜索的偏置较低,但方差较高,原因是柱搜索会尝试搜索更多的假设。因此,与直觉相反,一个学习能力更强的学习器并不见得比学习能力弱的效果更好。
图 2 示例说明了这一点(注:训练样例含有 64 个布尔类型特征和 1 个根据一个集合的“如果…那么…”的规则集合计算得到的布尔类型的类别。图中的曲线是对 100 次运行结果的平均,每次对应不同的随机产生的规则集合。误差条(error bar)代表两个标准方差。具体细节请参考论文【10】)。即使真正的分类器是一个规则集合,但根据 1000个样例学习的朴素贝叶斯学习器(摘注:原文Naive Bayes)仍比一个规则学习器的准确率更高。甚至当朴素贝叶斯错误地假设分类面是线性的,也依然如此。这种情形在机器学习领域很常见:一个强错误假设比那些弱正确假设更好,这是因为后者需要更多的数据才能避免过拟合。

交叉验证可以帮助避免过拟合,例如通过交叉验证来选择决策树的最佳大小。但这不能彻底解决问题,因为假如我们利用交叉验证做太多的参数选择,它本身就会开始过拟合【17】。
..................................
更多的数据胜过更聪明的算法
假设你已经尽你所能构建了最好的特征集合,但分类器的效果仍不够好,这时候应该怎么办呢?有两个主要选择:设计更好的学习算法,或者收集更多数据(包括更多的样例和不致造成维度灾难的更多可能的原始特征)。机器学习研究者更关注前者,但从实用角度来看,最快捷的方法是收集更多数据。作为一条经验,有大量数据的笨算法要胜过数据量较少的聪明算法。(毕竟,机器学习就是研究如何让数据发挥作用的。)
然而这带来了另外一个问题:可扩展性(scalability)。在绝大多数计算机科学问题中,两个主要资源是有限的——时间和内存。而在机器学习中,还有第三个:训练数据(摘注:原文training data )。其中哪一个资源会成为瓶颈是随着时间变化而不断变化的。在20世纪80年代,瓶颈是数据。现在的瓶颈则是时间。我们有海量数据,但没有足够的时间处理它们,只能弃之不用。这就造成一个悖论:即使理论上说,更多数据意味着我们可以学习更复杂的分类器,但在实践中由于复杂分类器需要更多的学习时间,我们只能选用更简单的分类器。一个解决方案是对复杂分类器提出快速学习算法,在这个方向上已经有了一些引人注目的进展(例如赫尔滕(Hulten)和多明戈斯(Domingos)的工作【11】)。
采用更聪明的算法得到的回报比预期要少,一部分原因是,机器学习的工作机制基本上是相同的。这个论断也许让你吃惊,特别是当你想到诸如规则集与神经网络之间差异巨大的表示方法的时候。但实际上,命题规则的确可以轻易地表示成神经网络,其他表示之间也有类似的关系。本质上所有的学习器都是将临近的样例归类到同一个类别中;关键的不同之处在于“临近”的意义。对于非均匀分布的数据,不同的学习器可以产生迥乎不同的分类边界,同时仍能在关心的领域(即那些有大量训练样例、测试样例也会有很大概率出现的领域)保证得到相的预测结果。这也有助于解释为什么能力强的学习器虽然不稳定却仍然很精确。图 3在二维空间展示了这一点,在高维空间这个效应会更强。

作为一条规则,首先尝试最简单的学习器总是有好处的(例如应该在逻辑斯蒂回归之前先尝试朴素贝叶斯,在支持向量机之前先尝试近邻 [ 摘注:原文, naïve Bayesbefore logistic regression, k-nearest neighbor beforesupport vector machines)])。更复杂的分类器固然诱人,但它们通常比较难驾驭,原因包括我们需要调节更多的参数才能得到好的结果,以及它们的内部机制更不透明。
学习器可以分为两大类:一类的表示是大小不变的,比如线性分类器(摘注:原文linear classifiers);另一类的表示会随着数据而增长,比如决策树(摘注:原文decisiontrees)。(后者有时候会被称为非参数化学习器(nonparametric learners),但不幸的是,它们通常需要比参数化学习器学习更多的参数。)数据超过一定数量后,大小不变的学习器就不能再从中获益。(注意图 2 中朴素贝叶斯的准确率是如何逼近大约 70%的。)而如果有足够的数据,大小可变的学习器理论上可以学习任何函数,但实际上却无法做到。这主要是受到算法(例如贪心搜索会陷入局部最优)和计算复杂度的限制。而且,由于维度灾难,再多的数据也不会够。正是由于这些原因,只要你努力,聪明的算法——那些充分利用已有数据和计算资源的算法——最后总能取得成功。在设计学习器和学习分类器之间并没有明显的界限;因为任何知识要么可以被编码进学习器,要么可以从数据中学到。所以,机器学习项目通常会有学习器设计这一重要部分,机器学习实践者应当在这方面积累一些专门知识【12】。
........................................................
简单并不意味着准确
著名的奥坎姆剃刀(occam’s razor)原理称:若无必要,勿增实体(entities should not be multi-plied beyond necessity)。在机器学习中,这经常被用来表示成:对于有相同训练误差的两个分类器,比较简单的那个更可能有较低的测试误差。关于这个断言的证明经常出现在文献中,但实际上对此有很多反例,而且“没有免费的午餐”定理也暗示了这个断言并不正确。
我们前面已经看到了一个反例:模型集成。集成模型的泛化误差会一直随着增加新的分类器而改进,甚至可以优于训练误差。另一个反例是支持向量机,它实际上可以有无限个参数而不至于过拟合。而与之相反,函数可以将轴上任意数量、任意分类的数据点划分开,即使它只有1个参数【23】。因此,与直觉相反,在模型参数的数量和过拟合之间并无直接联系。
一个更成熟的认识是将复杂度等同于假设空间的大小。这是基于以下事实:更小的假设空间允许用更短的代码表示假设。那么“理论保证”一节中的边界就暗示了,更短的假设可以泛化得更好。这还可以进一步改善为,为有先验偏好的空间中的假设分配更短的代码。但如果将此看作是准确(accuracy)和简单(simplicity)之间权衡的“证明”,那就变成循环论证了—— 我们将所偏好的假设设计得更加简单,而如果结果是准确的是因为我们的偏好是准确的,而不是因为这些假设在我们选择的表示方法中是“简单的”
............................................................
简单意味着较小的泛化误差,但有可能造成学习器本身的偏差很大。
..............................................................
相关并不意味着因果
相关不意味着因果,这一点经常被提起,好像在这儿已经不值得再加赘述了。但是,即使我们讨论的这些学习器只能学习到相关性,它们的结果也经常被作为因果关系来对待。这样做错了么?如果是错的,为什么人们还这样做呢?
更多时候,人们学习预测模型的目标是作为行动指南。如果我们发现超市里的啤酒和尿布经常被一起购买,那将啤酒放在尿布旁边将会提高销售量。(这是数据挖掘领域的著名例子。)但除非真的做实验,不然很难发现这一点。机器学习通常应用于观测(observational)数据,在观测数据中预测变量并不在学习器的控制之下,这与实验(experimental)数据相反,后者的预测变量在控制范围内。一些学习算法其实有潜力做到从观测数据发现因果信息,但它们的可用性比较差 【19】。而另一方面,相关性是因果关系的标志,我们可以将其作为进一步考察的指南(例如试图理解因果链可能是什么样)。
二、PAC学习理论
学习=PAC可学习=ε可学习
1.我们不要求学习器输出零错误率的假设,只要求错误率被限制在某常数ε范围内,ε可为任意小。
2.不要求学习器对所有任意抽取的数据都能成功预测,只要求其失败的概率被限定在某个常数μ的范围内,μ可取任意小。
3.简而言之,我们只要求学习器可能学习到一个近似正确的假设,故得到了“可能近似正确学习”或PAC学习。
PAC可学习的主要公式
下列公式是机器学习的泛化误差和一些学习器参数的关系
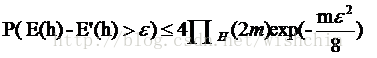
简单并不意味着准确
著名的奥坎姆剃刀(occam’s razor)原理称:若无必要,勿增实体(entities should not be multi-plied beyond necessity)。
在机器学习中,简单的算法意味着增长函数
较小,带入公式12,意味着相对较小的泛化误差。
但是简单的算法导致E’(h)较大,产生较大的训练误差,导致学习器变得没有实际意义。
更多的数据有更好的准确率
公式12中的m代表数据的个数,更大的m会产生更小的泛化误差。更多的数据胜过更聪明的算法。
相关并不意味着因果
假设空间的假设来源于大量的专家经验,认知体系试图用完备性诠释所观察到现象,并不能本质的了解现象的内在联系。归纳是认识的阶段性工作,完全认识依然需要遍历。
PAC学习理论:机器学习那些事的更多相关文章
- AI:PR的数学表示-传统方法PR
前言: 接上一篇:AI:模式识别的数学表示 在图像处理PR领域,相对于ANN方法,其他的方法一般称为传统方法.在结构上,几乎所有的PR方法都是可解释的.且任一传统方法,在一定约束下,可以转换为SV近邻 ...
- 【机器学习Machine Learning】资料大全
昨天总结了深度学习的资料,今天把机器学习的资料也总结一下(友情提示:有些网站需要"科学上网"^_^) 推荐几本好书: 1.Pattern Recognition and Machi ...
- 机器学习(Machine Learning)&深度学习(Deep Learning)资料【转】
转自:机器学习(Machine Learning)&深度学习(Deep Learning)资料 <Brief History of Machine Learning> 介绍:这是一 ...
- 机器学习(Machine Learning)与深度学习(Deep Learning)资料汇总
<Brief History of Machine Learning> 介绍:这是一篇介绍机器学习历史的文章,介绍很全面,从感知机.神经网络.决策树.SVM.Adaboost到随机森林.D ...
- [ML] Decision Tree & Ensembling Metholds
热身:分类问题若干策略 SVM, LR, Decision Tree的比较 同样是分类:SVM.LR.决策树,三者之间有什么优劣势呢? 答:Are decision tree algorithms l ...
- 几种Boost算法的比较(Discrete AdaBoost, Real AdaBoost, LogitBoost, Gentle Adaboost)
关于boost算法 boost算法是基于PAC学习理论(probably approximately correct)而建立的一套集成学习算法(ensemble learning).其根本思想在于通过 ...
- CNN for Visual Recognition (02)
图像分类 参考:http://cs231n.github.io/classification/ 图像分类(Image Classification),是给输入图像赋予一个已知类别标签.图像分类是计算机 ...
- PGM:图模型学习概述
http://blog.csdn.net/pipisorry/article/details/52571640 动机 前面我们讨论的问题出发点是给定一个图模型.如在独立性和推理讨论中,假定模型--结构 ...
- pgm13
这部分开始,我们将讨论 learning 相关的内容.PGM 为 frequentist 与 Bayesian 系的 model 提供了同一种语言,对前者来说 learning 就是确定一种对“未知但 ...
随机推荐
- 使用androidstudio 分析内存泄漏
分析内存泄漏 http://www.jianshu.com/p/c49f778e7acf
- (39.2). Spring Boot Shiro权限管理【从零开始学Spring Boot】
(本节提供源代码,在最下面可以下载) (4). 集成Shiro 进行用户授权 在看此小节前,您可能需要先看: http://412887952-qq-com.iteye.com/blog/229973 ...
- hdu_1232_畅通工程_201403091018
畅通工程 Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)Total Submis ...
- 洛谷 P1796 汤姆斯的天堂梦_NOI导刊2010提高(05)
P1796 汤姆斯的天堂梦_NOI导刊2010提高(05) 题目描述 汤姆斯生活在一个等级为0的星球上.那里的环境极其恶劣,每天12小时的工作和成堆的垃圾让人忍无可忍.他向往着等级为N的星球上天堂般的 ...
- Android:解决cannot find zipalign的问题
如果当前使用的Android SDK是v20的话,在通过Eclipse或者Intellij IDEA打包Android项目时,会出现一个”cannot find zipalign”的错误. 这个错误的 ...
- UITextView上加入默认文字
1. 实现UITextView的代理方法 text.view.delegate = self; 2. 在UITextView上覆盖UILabel ps:必须实现 label.enabled = NO; ...
- 一个NHibernate的BUG
一.背景 我们如今做的项目,用NHibernate实现数据訪问层. 訪问数据时,有的数据库表是确定的:有明白的表名.字段名.这时候依照常规的方法处理就可以:建立数据库表到类的映射.使用HQL读写数据库 ...
- 未能加载文件或程序集“System.Web.Helpers, Version=2.0.0.0
在本地终于用上了ASP.NET MVC4自带的认证功能,但放到生产服务器上就出问题了:打开注册页面没问题,但一点下注册按钮就报错了: 未能加载文件或程序集"System.Web.Helper ...
- Linux Framebuffer 驱动框架之一概念介绍及LCD硬件原理【转】
本文转载自:http://blog.csdn.net/liuxd3000/article/details/17464779 一.基本概念 帧缓冲(Framebuffer)是Linux系统为显示设备提供 ...
- C# WinForm小程序(技术改变世界-cnblog)
WinForm小程序(技术改变世界-cnblog) 需求: 1.点击按钮 更新 当前时间 2.输入 身份证,必须身份证 排序(类似银行卡那样的空格),自动生成空格排序 3.实现 必须按 第一个按 ...


