luogu1514 引水入城

题目大意

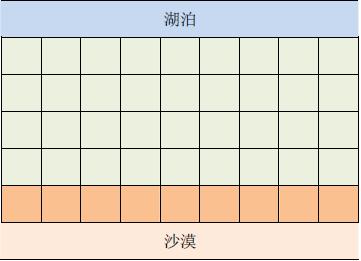
在一个遥远的国度，一侧是风景秀美的湖泊，另一侧则是漫无边际的沙漠。该国的行政区划十分特殊，刚好构成一个NN 行\times M×M 列的矩形，如上图所示，其中每个格子都代表一座城市，每座城市都有一个海拔高度。

为了使居民们都尽可能饮用到清澈的湖水，现在要在某些城市建造水利设施。水利设施有两种，分别为蓄水厂和输水站。蓄水厂的功能是利用水泵将湖泊中的水抽取到所在城市的蓄水池中。

因此，只有与湖泊毗邻的第11 行的城市可以建造蓄水厂。而输水站的功能则是通过输水管线利用高度落差，将湖水从高处向低处输送。故一座城市能建造输水站的前提，是存在比它海拔更高且拥有公共边的相邻城市，已经建有水利设施。由于第NN 行的城市靠近沙漠，是该国的干旱区，所以要求其中的每座城市都建有水利设施。那么，这个要求能否满足呢？如果能，请计算最少建造几个蓄水厂；如果不能，求干旱区中不可能建有水利设施的城市数目。

第二问思路

注意

　　说沙城构成连续的区间是在有解的情况下才成立的。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <functional>
#include <queue>
#include <cassert>
using namespace std;

#define Pair pair<int, int>
#define UpdateMin(x, y) x = min(x, y)
#define UpdateMax(x, y) x = max(x, y)

const int MAX_NODE = 510, INF = 0x3f3f3f3f;
const int Next[4][2] = { {0, 1}, {1, 0}, {0, -1}, {-1, 0} };
int A[MAX_NODE][MAX_NODE];
bool Vis[MAX_NODE][MAX_NODE];
bool Connect[MAX_NODE];
int TotRow, TotCol;

struct RangeCover
{
private:
    Pair ranges[MAX_NODE];
    int TotRange, L, R;

public:
    void Insert(Pair range)
    {
        ranges[++TotRange] = range;
    }

    int GetCnt()
    {
        sort(ranges + 1, ranges + TotRange + 1);
        ranges[++TotRange] = Pair(INF, INF);
        int lBegin = 1, p = 1, ans = 0;
        while (lBegin <= TotCol)
        {
            while (ranges[p + 1].first <= lBegin)
                p++;
            assert(ranges[p].first <= lBegin && ranges[p].second >= lBegin);
            ans++;
            lBegin = ranges[p].second + 1;
        }
        return ans;
    }
}g;

Pair Bfs(int startCol)
{
    for (int i = 1; i <= TotRow; i++)
        for (int j = 1; j <= TotCol; j++)
            Vis[i][j] = false;
    Pair ans(INF, -INF);
    static queue<Pair> q;
    while (!q.empty())
        q.pop();
    q.push(Pair(1, startCol));
    while (!q.empty())
    {
        Pair cur = q.front();
        q.pop();
        if (Vis[cur.first][cur.second])
            continue;
        Vis[cur.first][cur.second] = true;
        if (cur.first == TotRow)
        {
            Connect[cur.second] = true;
            UpdateMin(ans.first, cur.second);
            UpdateMax(ans.second, cur.second);
        }
        for (int i = 0; i < 4; i++)
        {
            int nextRow = cur.first + Next[i][0], nextCol = cur.second + Next[i][1];
            if (A[nextRow][nextCol] < A[cur.first][cur.second])
                q.push(Pair(nextRow, nextCol));
        }
    }
    return ans;
}

void Build()
{
    for (int i = 1; i <= TotCol; i++)
    {
        if ((i == 1 || A[1][i - 1] <= A[1][i])
            && (i == TotCol || A[1][i + 1] <= A[1][i]))
        {
            Pair lr = Bfs(i);
            if (lr.first < INF && lr.second > -INF)
                g.Insert(lr);
        }
    }
}

int Check()
{
    int ans = 0;
    for (int i = 1; i <= TotCol; i++)
        ans += (!Connect[i]);
    return ans;
}

int main()
{
    memset(A, INF, sizeof(A));
    scanf("%d%d", &TotRow, &TotCol);
    for (int i = 1; i <= TotRow; i++)
        for (int j = 1; j <= TotCol; j++)
            scanf("%d", &A[i][j]);
    Build();
    int failCnt = Check();
    if (failCnt > 0)
    {
        printf("0\n%d\n", failCnt);
        return 0;
    }
    printf("1\n%d\n", g.GetCnt());
    return 0;
}