BZOJ2142: 礼物（拓展lucas）

Description

一年一度的圣诞节快要来到了。每年的圣诞节小E都会收到许多礼物，当然他也会送出许多礼物。不同的人物在小E

心目中的重要性不同，在小E心中分量越重的人，收到的礼物会越多。小E从商店中购买了n件礼物，打算送给m个人

，其中送给第i个人礼物数量为wi。请你帮忙计算出送礼物的方案数（两个方案被认为是不同的，当且仅当存在某

个人在这两种方案中收到的礼物不同）。由于方案数可能会很大，你只需要输出模P后的结果。

Input

输入的第一行包含一个正整数P，表示模；

第二行包含两个整整数n和m，分别表示小E从商店购买的礼物数和接受礼物的人数；

以下m行每行仅包含一个正整数wi，表示小E要送给第i个人的礼物数量。

Output

若不存在可行方案，则输出“Impossible”，否则输出一个整数，表示模P后的方案数。

Sample Input

100
4 2
1
2

Sample Output

12

解题思路：

这道题就是组合数取模终极版。

很显然要求的就是：

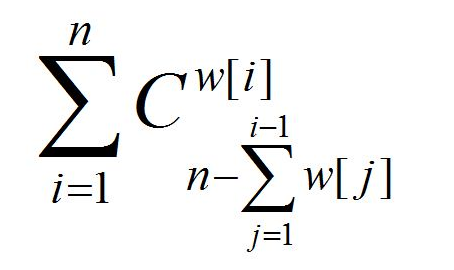
数据范围好像不是很大。

拓展lucas没跑了。

大概思路就是：先将取模数拆分，求出各部分的解，使用中国剩余定理合并答案。

中国剩余定理我就不说了。

这里主要讲一下拓展lucas。

将组合数展开：

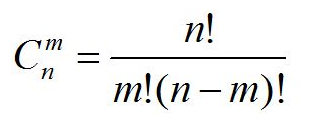
这里主要有两个问题需要解决

1.n 太大，一锅煮不下，直接枚举会超时。

2.n 比取模数大时会变成0下面本来有抵消的都没了。

我们一个一个看。

怎么计算n!呢？

我们暴力吧。

我们先看第二个吧。

先说第二个。

既然是抵消了，那么为何不让它先约掉呢。

很显然，将最小质因数p的幂次项提取出就可以完成任务。

也就是说，在处理阶乘时，跳过幂次项。

就是将原式化简成这样：

就解决了。

回来看第一个。

既然要跳过p的次幂，那么就都提出来发现剩余项是前p^k以内的数的次幂。

提出来的项可以递归操作。

差不多就是这样了。

我也不知道这和lucas有啥关系

代码：

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 typedef long long lnt;
 lnt prime[];
 lnt picie[];
 lnt tmp[];
 lnt w[];
 lnt n,m;
 int cnt;
 lnt qucp(lnt a,lnt b,lnt c)
 {
     lnt ans=;
     while(b)
     {
         if(b&)
             ans=ans*a%c;
         a=a*a%c;
         b=b/;
     }
     return ans%c;
 }
 void exgcd(lnt a,lnt b,lnt &x,lnt &y)
 {
     if(!b)
     {
         x=;
         y=;
         return ;
     }
     exgcd(b,a%b,y,x);
     y-=a/b*x;
     return ;
 }
 lnt Inv(lnt x,lnt mod)
 {
     lnt a;
     lnt b;
     exgcd(x,mod,a,b);
     return (a%mod+mod)%mod;
 }
 lnt Crt(lnt num,lnt *ans,lnt *mod)
 {
     lnt ret=;
     lnt mdl=;
     for(int i=;i<=num;i++)
         mdl*=mod[i];
     for(int i=;i<=num;i++)
     {
         lnt x=mdl/mod[i];
         ret=(ret+x*Inv(x,mod[i])%mdl*ans[i]%mdl)%mdl;
     }
     return ret;
 }
 lnt fac(lnt len,lnt pi,lnt pk)
 {
     if(!len)
         return ;
     lnt ans=;
     for(int i=;i<=pk;i++)
         if(i%pi)
             ans=ans*i%pk;
     ans=qucp(ans,len/pk,pk);
     for(int i=;i<=len%pk;i++)
         if(i%pi)
             ans=ans*i%pk;
     return ans*fac(len/pi,pi,pk)%pk;
 }
 lnt Exlucas(lnt n,lnt m,lnt plc)
 {
     if(m>n)
         return ;
     lnt fan=fac(n,prime[plc],picie[plc]);
     lnt fam=fac(m,prime[plc],picie[plc]);
     lnt fad=fac(n-m,prime[plc],picie[plc]);
     lnt ans=fan*Inv(fam,picie[plc])%picie[plc]*Inv(fad,picie[plc])%picie[plc];
     lnt c=;
     for(int i=n;i;i/=prime[plc])
         c+=i/prime[plc];
     for(int i=m;i;i/=prime[plc])
         c-=i/prime[plc];
     for(int i=n-m;i;i/=prime[plc])
         c-=i/prime[plc];
     return ans*qucp(prime[plc],c,picie[plc])%picie[plc];
 }
 void brkdn(lnt P)
 {
     for(int i=;i*i<=P;i++)
     {
         if(P%i==)
         {
             cnt++;
             prime[cnt]=i;
             picie[cnt]=;
             while(P%i==)
             {
                 picie[cnt]*=(lnt)(i);
                 P/=i;
             }
         }
     }
     if(P!=)
     {
         cnt++;
         picie[cnt]=prime[cnt]=P;
     }
     return ;
 }
 int main()
 {
     lnt Mod;
     scanf("%lld",&Mod);
     brkdn(Mod);
     scanf("%lld%lld",&n,&m);
     lnt sum=;
     lnt ans=;
     for(int i=;i<=m;i++)
     {
         scanf("%lld",&w[i]);
         sum+=w[i];
     }
     if(sum>n)
     {
         puts("Impossible");
         return ;
     }
     for(int i=;i<=m;i++)
     {
         for(int j=;j<=cnt;j++)
             tmp[j]=Exlucas(n,w[i],j);
         ans=ans*Crt(cnt,tmp,picie)%Mod;
         n-=w[i];
     }
     printf("%lld\n",ans);
     return ;
 }