K:Union-Find(并查集)算法
相关介绍:
并查集的相关算法,是我见过的,最为之有趣的算法之一。并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。其相关的实现代码较为简短,实现思想也简单易懂,处理问题的效率也高,解决的问题范围也较广。
为了实现并查集的相关算法,我们规定将对象称之为触点,将整数对称之为连接,将两两之间彼此互不相连的各个集合的分布(也就是其相关的等价类)称之为连通分量,也称为分量。同时定义了如下的API用来封装其所需的基本操作:
public class UF
| 相关API | 说明 |
|---|---|
| UF(int N) | 以整数标识(0到N-1)初始化N个触点 |
| void union(int p,int q) | 在p和q之间添加一条连接,也就是连接p和q |
| int find(int p) | p(0到N-1)所在的分量的标识 |
| boolean connected(int p,int q) | 如果p和q存在同一个分量中则返回true |
| int count() | 连通分量的数量 |
下图1.1用以说明触点,连接,和连通分量:
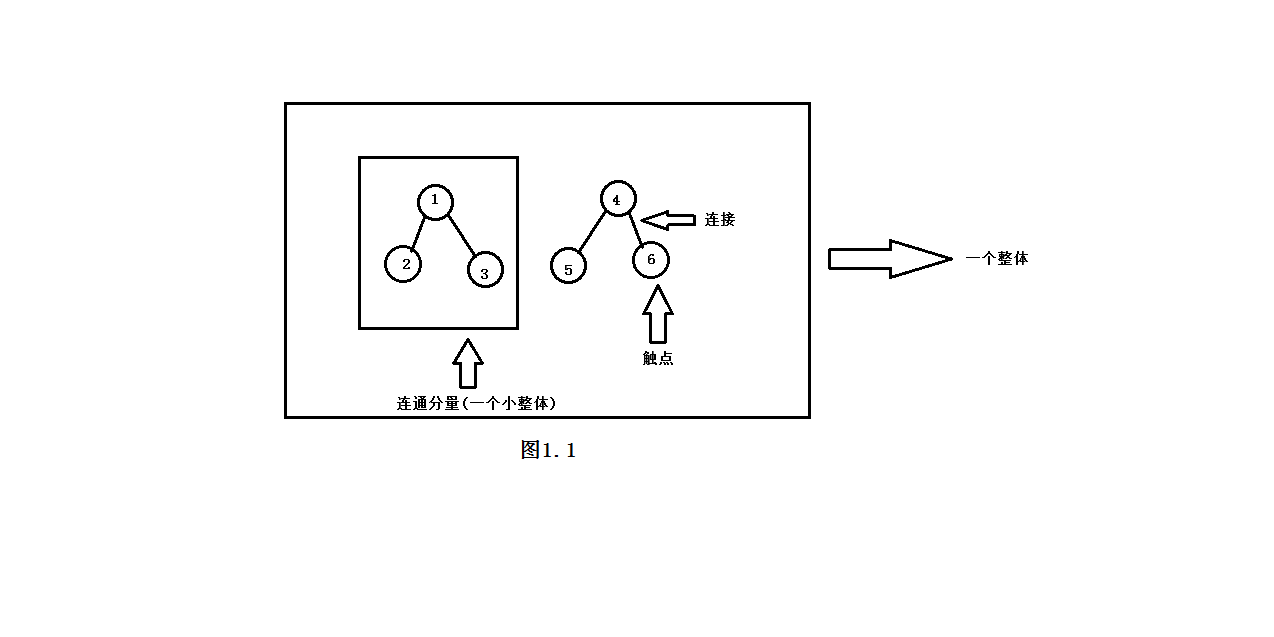
我们用整数int来表示相关的触点以及分量。为此,我们可以用一个以触点为索引(也就是下标)的数组id[]来表示所有的分量。我们将使用分量中的某个触点的名称作为分量的标识符,因此,你可以认为每个分量都是由它的触点之一来进行表示的。一开始我们有N个分量,每个触点都构成了触点i,我们将用find()方法用来判定它所在的分量所需的信息保存在id[i]之中。connected(int p,int q)方法的实现只用到了一条语句find(p)==find(q),它将返回布尔值。find(int p)方法和union(int p,int q)方法的实现是整个Union-Find相关算法的关键。我们在实现时,采用int数组id用于表示相关的连通分量的信息,一个整型变量count用于记录连通分量的个数。
以下代码为相关API中的部分API的实现
相关代码:
package algorithm;
/**
* 用于演示并查集(Union-Find)算法
* @author 学徒
*
*/
public abstract class UF
{
protected int[] id;//分量id(以触点为索引)
protected int count;//分量数目
public UF(int N)
{
//初始化分量id数组
count=N;
id=new int[N];
for(int i=0;i<N;i++)
{
id[i]=i;
}
}
public int count()
{
return count;
}
public boolean connected(int p,int q)
{
return find(p)==find(q);
}
public abstract int find(int p);
public abstract void union(int p,int q);
}
以下,我们将讨论四种不同的find(int p)和union(int p,int q)方法的实现,它们均根据以触点为索引的id[]数组来确定两个触点是否保存在相同的连通分量中,这四种不同的实现分别为quick-find、quick-union、加权quick-union、路径压缩的加权quick-union
quick-find算法:
该算法所采用的思想是保证当且仅当id[p]等于id[q]时,p和q是连通的。换句话说,在同一个连通分量中的所有触点,其相应的id[]中的值必须全部相同。为了确保调用union(int p,int q)时保证这一点,我们首先检查它们是否已经在同一连通分量中,如果在同一个连通分量中,我们就不采取任何行动,否则,我们面对的情况是p所在的连通分量中的所有触点的id[]值均为同一个值,而q所在的连通分量中的所有触点均为另一个值。要将两个分量合二为一,我们必须将两个集合中所有的触点所对应的id[]元素的值变为同一个值。为此,我们需要遍历整个数组,将所有和id[p]相等的元素的值变为id[q]的值。我们也可以将所有和id[q]相等的元素的值变为id[p]值,两者皆可。
相关代码:
class Quick_Find extends UF
{
public Quick_Find(int N)
{
super(N);
}
@Override
public int find(int p)
{
return id[p];
}
@Override
public void union(int p, int q)
{
//检查p和q相关的连通分量的标识
int pID=find(p);
int qID=find(q);
//如果p和q已经在相同的分量之中,则不需要采取任何的行动
if(pID==qID)
return;
//将p的分量重命名为q的分量的标识
for(int i=0;i<id.length;i++)
{
if(id[i]==pID)
id[i]=qID;
}
count--;
}
}
分析:
从上面的代码可知,find()的操作速度显然是很快的,因为其只需要访问id[]数组一次,其时间复杂度为O(1),而union算法的时间复杂度为O(N)。但quick-find算法无法处理大型问题,因为对于每一对输入union()都需要扫描整个id[]数组。为此,当使用quick-find算法来解决问题的时候,特别是最后只是得到一个连通分量的问题的时候,其时间复杂度为O(N^2)。
quick-union算法:
该算法的目的在于提高union算法的速度,其与quick-find算法是互补的。他们基于相同的数据结构——以触点为索引的id[] 数组。但其数组中相关的值的含义却并不相同,我们需要用它来定义更加复杂的结构。确切的说,每个触点所对应的id[]都是同一个分量中的另一个触点的名称(也可能是自己)我们将这种联系称之为链接。在实现find()方法时,我们从给定的触点开始,由它链接得到另一个触点,再由这个触点的链接到达第三个触点,如此继续跟随着链接直到到达一个根触点,即链接指向自己的触点,该触点的标号同时也是该分量的标识。当且仅当分别由两个触点开始的这个过程到达了同一个根触点时,它们存在于同一个连通分量中。
相关代码:
class Quick_Union extends UF
{
public Quick_Union(int N)
{
super(N);
}
@Override
public int find(int p)
{
//找出该连通分量的标识,即连接指向自身的节点的标号
while(p!=id[p])
p=id[p];
return p;
}
@Override
public void union(int p, int q)
{
int pRoot=find(p);
int qRoot=find(q);
if(pRoot==qRoot)
return;
id[pRoot]=qRoot;
count--;
}
}
其union过程如下示意图1.2所示:
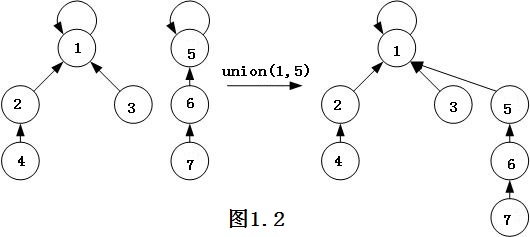
由于每个触点初始化之前均指向自身,为此,当每次union操作时,均会消除掉一个指向自身的触点,使得其中一个触点指向另一个指向自身的触点。我们可以将每个指向自身的触点的分量看成是一个整体,通过归纳,可以得知,无论从该连通分量的哪个触点出发进行find()操作,沿着其相关的链接进行查找。到最后总是可以找到其指向自身的一个触点,即为根触点,也就是该连通分量的标记。
分析:
quick-union算法看起来比quick-find算法快很多,因为它并不需要为每对输入遍历整个数组。在最好的情况,find()只需要访问数组一次就能够得到一个触点所在的连通分量的标记符;而在最坏的情况下,需要O(N)次访问(由于在初始时,每个触点均指向自身,若从开始到结束,在每次union的时候,将多个触点的连通分量链接到只有一个触点的连通分量的时,会出现连通分量合并成为一条“链”的情况,如图1.3所示)。为此,当使用quick-union算法对问题进行处理并最终只得到一个连通分量的时候,时间复杂度在最坏情况下为O(N^2)。出现这一种情况的根本原因在于进行union处理的时候,每次都将深度较深的连通分量所表示的树,链接到深度较浅的连通分量所代表的树中。为此,提出了如下的“加权quick-union”算法
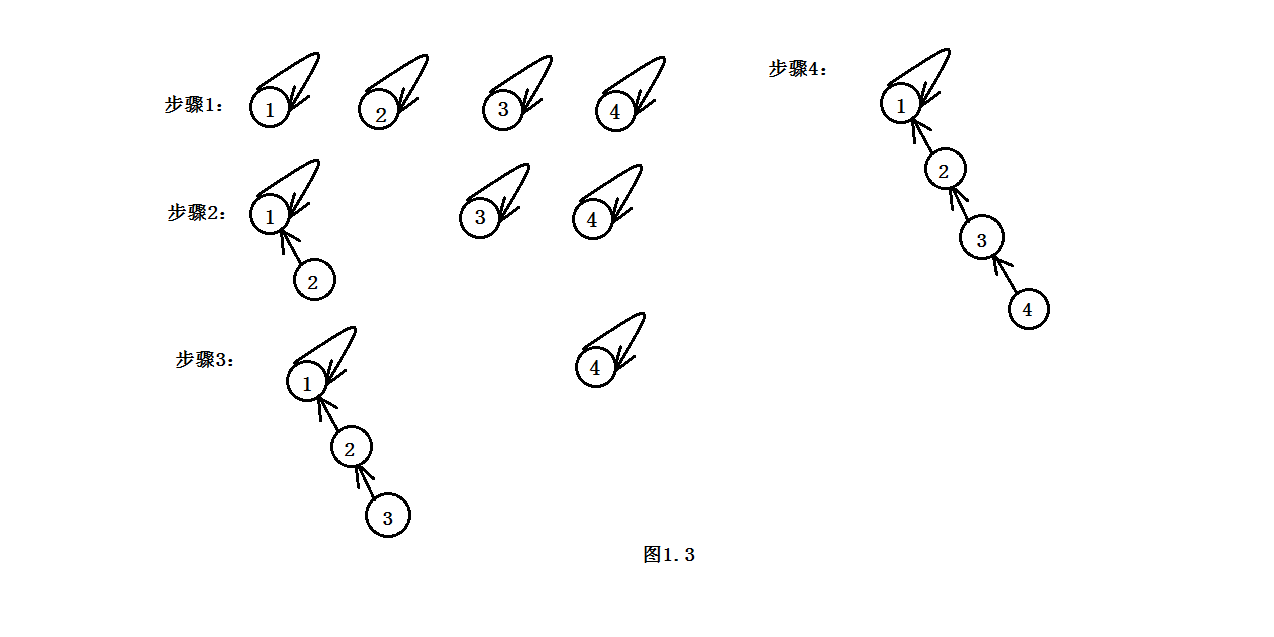
加权quick-union算法:
加权quick-union算法是在quick-union算法的基础上进行改进的。其在quick-union的基础上做出的改变的是,与其在union()中随意的将一棵树连接到另外的一棵树,不如记录每一棵树的大小并总是将较小的树连接到较大的树上。这项改动需要添加一个额外的数组和一些代码来记录数中的节点数。
相关代码:
class WeightQuick_Union extends UF
{
private int[] sz;//(由触点索引的)各个根节点所对应的分量的大小
public WeightQuick_Union(int N)
{
super(N);
sz=new int[N];
for(int i=0;i<N;i++)
{
sz[i]=1;
}
}
@Override
public int find(int p)
{
while(p!=id[p])
p=id[p];
return p;
}
@Override
public void union(int p, int q)
{
int i=find(p);
int j=find(q);
if(i==j)
return;
//将小树的根节点连接到大数的根节点
if(sz[i]<sz[j])
{
id[i]=j;
sz[j]+=sz[i];
}
else
{
id[j]=i;
sz[i]+=sz[j];
}
count--;
}
}
分析:
加权quick-union算法能够保证对数级别的性能。因为对于N个触点,加权quick-union算法构造的森林中的任意节点的深度最多为lgN。其证明过程如下:
证明:
可以通过归纳法证明一个更强的命题,即森林中大小为k的树的高度最多为lgk。在原始情况下,当k等于1时树的高度为0.根据归纳法,我们假设大小为i的树的高度最多为lgi,其中i < k。设i <= j且i+j=k,当我们将大小为i和大小为j的树归并时,小树中的所有节点的深度都增加了1,但它们现在所在的树的大小为i+j=k,而1+lgi=lg(i+i)<=lg(i+j)=lgk,性质成立。
路径压缩的quick-union算法:
虽然,加权quick-union算法能够保证在lgN的时间复杂度内解决问题,但是,仍然存在着一种比加权quick-union算法时间复杂度更低的算法,那就是使用路径压缩的quick-union算法。理想情况下,我们希望每个触点都直接的连接到其根节点上,但我们又不想像quick-find算法那样通过修改大量的连接而达到目的。于是,出现了一种接近这种理想状态的方法,那就是在检查触点的同时,把他直接连接到根节点上。该方法只需要在find(int p)中为其添加上一个循环,将在路径上遇到的所有节点都直接链接到其根节点上,这样我们所得到的结果是几乎完全扁平化的树。
相关代码:
class PathCompressWeightQuick_Union extends UF
{
private int[] sz;//(由触点索引的)各个根节点所对应的分量的大小
public PathCompressWeightQuick_Union(int N)
{
super(N);
sz=new int[N];
for(int i=0;i<N;i++)
{
sz[i]=1;
}
}
@Override
public int find(int p)
{
int temp=p;
//运行结束后,p节点存储的为其根节点
while(p!=id[p])
p=id[p];
while(temp!=p)
{
//用于记录当前节点p的父节点的编号
int parent=id[temp];
//将当前节点直接指向其根节点
id[temp]=p;
temp=parent;
}
return p;
}
@Override
public void union(int p, int q)
{
int i=find(p);
int j=find(q);
if(i==j)
return;
//将小树的根节点连接到大数的根节点
if(sz[i]<sz[j])
{
id[i]=j;
sz[j]+=sz[i];
}
else
{
id[j]=i;
sz[i]+=sz[j];
}
count--;
}
}
分析:
使用路径压缩的加权quick-union算法,其均摊后的成本非常非常的接近但仍没能达到常数级别(O(1))。
并查集的使用场景举例:
在学到一个知识点的时候,我们可能会常常思考一个问题,那就是它有什么用?并查集也不例外,为了说明并查集的相关作用。此处,举了一些简单的例子,用以说明并查集的使用场景及其相关的作用,在举例的时候,使用整数来表示问题中的集合的每个单位。
网络: 输入的整数表示的是大型计算机网络中的计算机,而整数对则表示网络中的连接。使用并查集能够帮助我们判定在两台计算机P和q之间是否需要架设一条新的连接才能够进行通信,或者是我们可以通过已有的连接在两者之间建立通信线路;或者这些整数表示的可能是电子电路中的触点,而整数对表示的是连接触点之间电路;或者这些整数表示的可能是社交网络中的人,而整数对表示的是朋友关系,使用并查集,我们可以知道社交网络上的任意两个人之间,是否可以通过已知的连接发生联系。
变量名等价性: 某些编程环境允许声明两个等价的变量名(指向同一个对象的多个引用)。在一系列这样的声明之后,系统需要判断两个给定的变量名是否等价。这种较早出现的应用(如FORTRAN语言)推动了并查集相关的算法的发展。
数学集合: 在更高的抽象层次上,可以将输入的所有整数看做属于不同的数学集合。在处理一个整数对P和q时,我们是在判断它们是否属于相同的集合。如果不是,我们会将p所属的集合和q所属的集合归并到同一个集合中。该方式也是个人认为的,用于思考一个问题是否可以通过使用并查集来解决的最后的方式,先把问题进行抽象化,当问题抽象化成判断两个集合是否同属于一个集合的问题的时候,可以采用并查集来进行解决。
相关资料:《算法》 第四版
K:Union-Find(并查集)算法的更多相关文章
- Union-Find 并查集算法
一.动态连通性(Dynamic Connectivity) Union-Find 算法(中文称并查集算法)是解决动态连通性(Dynamic Conectivity)问题的一种算法.动态连通性是计算机图 ...
- 并查集算法Union-Find的思想、实现以及应用
并查集算法,也叫Union-Find算法,主要用于解决图论中的动态连通性问题. Union-Find算法类 这里直接给出并查集算法类UnionFind.class,如下: /** * Union-Fi ...
- hdu 1232 畅通工程(并查集算法)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1232 畅通工程 Time Limit: 4000/2000 MS (Java/Others) M ...
- POJ2985 The k-th Largest Group[树状数组求第k大值+并查集||treap+并查集]
The k-th Largest Group Time Limit: 2000MS Memory Limit: 131072K Total Submissions: 8807 Accepted ...
- codeforces1156D 0-1-Tree 并查集
题目传送门 题意: 给定一棵n个点的边权为0或1的树,一条合法的路径(x,y)(x≠y)满足,从x走到y,一旦经过边权为1的边,就不能再经过边权为0的边,求有多少边满足条件? 思路: 首先这道题,换根 ...
- <算法><Union Find并查集>
Intro 想象这样的应用场景:给定一些点,随着程序输入,不断地添加点之间的连通关系(边),整个图的连通关系也在变化.这时候我们如何维护整个图的连通性(即判断任意两个点之间的连通性)呢? 一个比较简单 ...
- hdu 1213 How Many Tables(并查集算法)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=1213 How Many Tables Time Limit: 2000/1000 MS (Java/O ...
- 并查集(Union/Find)模板及详解
概念: 并查集是一种非常精巧而实用的数据结构,它主要用于处理一些不相交集合的合并问题.一些常见的用途有求连通子图.求最小生成树的Kruskal 算法和求最近公共祖先等. 操作: 并查集的基本操作有两个 ...
- 并查集(Union-Find) 应用举例 --- 基础篇
本文是作为上一篇文章 <并查集算法原理和改进> 的后续,焦点主要集中在一些并查集的应用上.材料主要是取自POJ,HDOJ上的一些算法练习题. 首先还是回顾和总结一下关于并查集的几个关键点: ...
- 【lazy标记得思想】HDU3635 详细学习并查集
部分内容摘自以下大佬的博客,感谢他们! http://blog.csdn.net/dm_vincent/article/details/7769159 http://blog.csdn.net/dm_ ...
随机推荐
- Linux中MySQL5.6编译安装与MySQL5.7二进制安装步骤
首先,介绍一下MySQL的几种安装方式 1.RPM.Yum 的安装方式:安装方便.安装速度快,无法定制 2.二进制:不需要安装,解压即可使用,不能定制功能 3.编译安装:可定制,安装慢. 编译安装中需 ...
- 如何用shell脚本取出服务器图片
一 ,SHELL 是什么 (1)shell是一种命令行解释器. (2)是用户和Linux内核之间沟通的桥梁,属于中间件.见下图 (3)交互流程:shell接受用户输入的指令 =>将指令传达给Li ...
- [Elasticsearch] 邻近匹配 (二) - 多值字段,邻近程度与相关度
多值字段(Multivalue Fields) 在多值字段上使用短语匹配会产生古怪的行为: PUT /my_index/groups/1 { "names": [ "Jo ...
- 《Deep Learning》译文 第一章 前言(中) 神经网络的变迁与称谓的更迭
转载请注明出处. 第一章 前言(中) 1.1 本书适合哪些人阅读? 能够说本书的受众目标比較广泛,可是本书可能更适合于例如以下的两类人群.一类是学习过与机器学习相关课程的大学生们(本科生或者研究生). ...
- SpringMVC上传图片并压缩及剪切demo
/** * */ package com.up.controller; import java.awt.Image; import java.awt.image.BufferedImage; impo ...
- vue中使用keepAlive组件缓存遇到的坑
项目开发中在用户由分类页category进入detail需保存用户状态,查阅了Vue官网后,发现vue2.0提供了一个keep-alive组件. 上一篇讲了keep-alive的基本用法,现在说说遇到 ...
- linux启动失败
如图 1.开机界面 按 e 键 2.选择第二个进入就好了 根据网上说的修改kernel 配置 加上 enforcing=0 无效 1.进入界面后再按 e 键 3.选择第二个按e键进入编辑 界面 每次 ...
- ConcurrentDictionary内部函数的使用说明
AddOrUpdate(...)函数的使用: private static ConcurrentDictionary<long, string> condic = new Concurre ...
- C#Lambda表达式Aggregate的用法及内部运行方式的猜想
, , , , }; // 其和为15 var count = nums.Aggregate((body, next) => { // 注意,nums的元素个数至少一个以上(但如果是有seed的 ...
- ABP .Net Core Entity Framework迁移使用MySql数据库
一.迁移说明 ABP模板项目Entity Framework Core默认使用的是Sql Server,也很容易将数据库迁移到MySQL,步骤如下. 二.迁移MySQL步骤 1. 下载项目 请到 ht ...
