关于原根的存在性及个数（Primitive Root Theorem）
我在RSA学习总结的第三部分关于Mille-Rabin素数测试的正确性证明里需要用到此定理，由于证明太长，故另开一章于此。（为啥我说话突然文绉绉了Orz，可能是这周辩论打多了）
结论是对素数p，modulo p的原根存在，个数为与ø（p-1），modulo p2的原根个数为(p-1)ø（p-1）个
对奇素数p，modulo p^n的原根存在，个数为pn-2(p-1)ø（p-1） (n>=3)
首先证明对任意素数p，modulo p的原根存在
以下是证明思路（符号的意思在第二张图，完整证明里有）
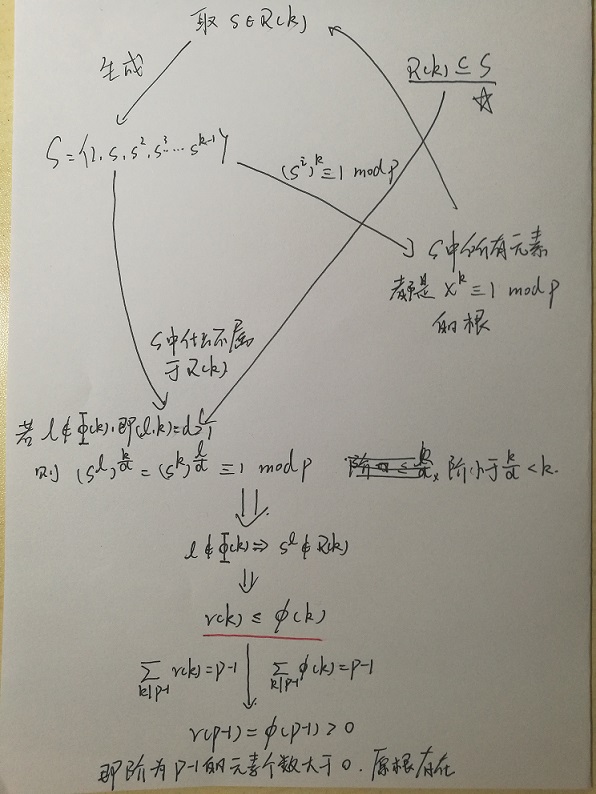
知道了modulo p^2下Primitive root存在后可以推广至p^n
关于原根的存在性及个数（Primitive Root Theorem）的更多相关文章
- 原根的存在性及个数证明（Primitive Root Theorem）
我在RSA学习总结的第三部分关于Mille-Rabin素数测试的正确性证明里需要用到此定理,由于证明太长,故另开一章于此.(为啥我说话突然文绉绉了Orz,可能是这周辩论打多了) 结论是对素数p,mod ...
- SPOJ3713——Primitive Root
终于有一个SPOJ题目是我自己独立做出来的,ORZ,太感动了. 题目意思是给你一个素数,问你一个数r是否满足,r,r^2,r^3,……,r^p-1,全不相同. 以前做过这种类型的题目额.是这样的. 根 ...
- POJ 1284：Primitive Roots（素数原根的个数）
Primitive Roots Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 5709 Accepted: 3261 Descr ...
- 【HDU 4992】 Primitive Roots （原根）
Primitive Roots Description We say that integer x, 0 < x < n, is a primitive root modulo n i ...
- poj 1284 Primitive Roots （原根）
Primitive Roots http://poj.org/problem?id=1284 Time Limit: 1000MS Memory Limit: 10000K Descr ...
- POJ1284 Primitive Roots [欧拉函数，原根]
题目传送门 Primitive Roots Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 5434 Accepted: ...
- POJ 1284：Primitive Roots 求原根的数量
Primitive Roots Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 3381 Accepted: 1980 D ...
- POJ 1284 Primitive Roots 数论原根。
Primitive Roots Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 2479 Accepted: 1385 D ...
- POJ_1284 Primitive Roots 【原根性质+欧拉函数运用】
一.题目 We say that integer x, 0 < x < p, is a primitive root modulo odd prime p if and only if t ...
随机推荐
- CSS边框（圆角、阴影、背景图片）
1.圆角 border-radius是向元素添加圆角边框. 使用方法: border-radius:10px; /* 所有角都使用半径为10px的圆角 */ border-radius: 5px 4 ...
- [Open Source] .NET 基于StackExchange.Redis的扩展
目录 简介 主从复制 备份与恢复 API AddOrUpdate GetOrAdd DeleteByPattern SearchKeys TransExcute Subscribe/Publish T ...
- 认识cpu、核与线程
作为一个后台开发人员,我想有必要了解这些基础知识.如果本文有不严谨或者疏忽的地方,请指正. cpu与核心 物理核 物理核数量=cpu数(机子上装的cpu的数量)*每个cpu的核心数 虚拟核 所谓的4核 ...
- 【Owin 学习系列】1. 第一个 Owin 程序
IIS 中的 Owin 在 IIS 里面部署 Owin,既能得到 Owin 管道模型的灵活性和模块特性,也能很好地利用 IIS 成熟的配置,Owin 程序将会跑在 ASP.NET request 的管 ...
- css 过渡和 变形
一.过渡(transition) transition-property: 指定具有过渡效果的CSS样式属性名 1.默认值: all 2.仅具有中间值(CSS样式值是数值的)的CSS样式具有过渡效果 ...
- css实现接地气的checkbox框
1.前言 我做的项目中,很少默认用原生的样式,甚至连下拉框都很少用select框,不过,原生也有原生的好处,来得快,没有什么大问题.如果是自己用html+css去拼接的话,样式会好看一点.不过应人而异 ...
- Android学习笔记-Button(按钮)
Button是TextView的子类,所以TextView上很多属性也可以应用到Button 上!我们实际开发中对于Button的,无非是对按钮的几个状态做相应的操作,比如:按钮按下的时候 用一种颜色 ...
- 初探Matplotlib
初探Matplotlib 例子来自此书: <Python编程从入门到实战>[美]Eric Matthes 使用pyplot绘图,一般的导入方法import matplotlib.pyplo ...
- Round #427 A. Key races(Div.2)
time limit per test 1 second memory limit per test 256 megabytes input standard input output stand ...
- Hibernate三大类查询总结
Hibernate目前总共分为三大类查询:cretiria,hql,本地sql [以下篇章搜集于网络,感谢作者] 第一:关于cretiria的查询 具有一个直观的.可扩展的条件查询API是Hibern ...