51Nod 1352 集合计数 扩展欧几里得

基准时间限制：1 秒 空间限制：131072 KB 分值: 20 难度：3级算法题
给出N个固定集合{1，N},{2,N-1},{3,N-2},...,{N-1,2},{N,1}.求出有多少个集合满足：第一个元素是A的倍数且第二个元素是B的倍数。
提示：
对于第二组测试数据，集合分别是：{1,10},{2,9},{3,8},{4,7},{5,6},{6,5},{7,4},{8,3},{9,2},{10,1}.满足条件的是第2个和第8个。

Input
第1行：1个整数T（1<=T<=50000)，表示有多少组测试数据。
第2 - T+1行：每行三个整数N，A,B（1<=N，A，B<=2147483647)
Output
对于每组测试数据输出一个数表示满足条件的集合的数量，占一行。
Input示例
2
5 2 4
10 2 3
Output示例
1
2
思路：
设A的倍数x，B的倍数y，则有Ax+By=N+1
利用exgcd，求Ax+By=gcd(A,B)的解，在求出符合题意最小的x
要注意x==0的情况是不符合题意的
判断第一组解是否符合题意，不符合
然受剩余的部分除以lcm(A,B)即可得到
注：最后除以lcm的证明
证：当x为最小正整数的第一组解符合题意的时候有（设此时为x0，y0）：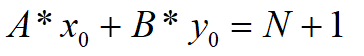

设增量为k,则有：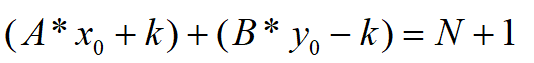

此时仍要满足以下等式：

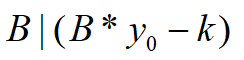
对于第一个式子，显然A*x0满足条件，即需要满足：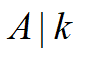

同理有：

所以k最小为lcm(A,B)

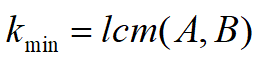
代码：

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 ll exgcd(ll a, ll b, ll &x, ll&y) {
     if(!b) {
         x=;
         y=;
         return a;
     }
     ll ans=exgcd(b,a%b,x,y);
     ll temp=x;
     x=y;
     y=temp-a/b*y;
     return ans;
 }
 int main() {
     ios::sync_with_stdio(false);
     ll T,N,A,B,x,y,sum;
     cin>>T;
     while(T--) {
         sum=;
         cin>>N>>A>>B;
         ll g=exgcd(A,B,x,y);
         if((N+)%g!=) {
             cout<<""<<endl;
             continue;
         }
         x=(N+)/g*x;
         ll b2=B/g;
         x=(x%b2+b2)%b2;
         if(!x) x=b2;
         y=(N+-x*A)/B;
         if(x>=&&x*A<=N&&y>=&&y*B<=N&&((x*A+y*B)==(N+)))
             sum++;
         else {
             cout<<""<<endl;
             continue;
         }
         ll lcm;
         if(!A/g) lcm=A/g*B;
         else lcm=B/g*A;
         ll t=(N-x*A)/lcm;
         if(t>) sum+=t;
         cout<<sum<<endl;
     }
     return ;
 }