字符串处理------Brute Force与KMP

一，字符串的简单介绍

例：POJ1488 　　http://poj.org/problem?id=1488

题意：替换文本中的双引号；

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;

int main()
{
    char c,flag=1;
    //freopen("Atext.in","r",stdin);
    while((c=getchar())!=EOF){
        if(c=='"'){printf("%s",(flag? "``" : "''"));flag=!flag;}
        else    printf("%c",c);
    }
    return 0;
}

二，模式匹配------Brute Force与KMP简介

1，Brute Force算法

例：POJ3080　　http://poj.org/problem?id=3080 枚举，BF

新：strstr(str1,str2) 函数用于判断字符串str2是否是str1的子串。如果是，则该函数返回str2在str1中首次出现的地址；否则，返回NULL。

Blue Jeans

Description

The Genographic Project is a research partnership between IBM and The National Geographic Society that is analyzing DNA from hundreds of thousands of contributors to map how the Earth was populated. 

As an IBM researcher, you have been tasked with writing a program that will find commonalities amongst given snippets of DNA that can be correlated with individual survey information to identify new genetic markers. 

A DNA base sequence is noted by listing the nitrogen bases in the order in which they are found in the molecule. There are four bases: adenine (A), thymine (T), guanine (G), and cytosine (C). A 6-base DNA sequence could be represented as TAGACC. 

Given a set of DNA base sequences, determine the longest series of bases that occurs in all of the sequences.

Input

Input to this problem will begin with a line containing a single integer n indicating the number of datasets. Each dataset consists of the following components:

• A single positive integer m (2 <= m <= 10) indicating the number of base sequences in this dataset.
• m lines each containing a single base sequence consisting of 60 bases.

Output

For each dataset in the input, output the longest base subsequence common to all of the given base sequences. If the longest common subsequence is less than three bases in length, display the string "no significant commonalities" instead. If multiple subsequences of the same longest length exist, output only the subsequence that comes first in alphabetical order.

Sample Input

3
2
GATACCAGATACCAGATACCAGATACCAGATACCAGATACCAGATACCAGATACCAGATA
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
3
GATACCAGATACCAGATACCAGATACCAGATACCAGATACCAGATACCAGATACCAGATA
GATACTAGATACTAGATACTAGATACTAAAGGAAAGGGAAAAGGGGAAAAAGGGGGAAAA
GATACCAGATACCAGATACCAGATACCAAAGGAAAGGGAAAAGGGGAAAAAGGGGGAAAA
3
CATCATCATCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCCC
ACATCATCATAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
AACATCATCATTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTTT

Sample Output

no significant commonalities
AGATAC
CATCATCAT

Source

South Central USA 2006

#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;

int main()
{
    //freopen("Atext.in","r",stdin);
    int n,m,len;
    char ans[70],s[15][65],tmp[65];
    cin >> n;
    while(n--){
        cin >> m;
        int k=3,flag=0;        //枚举的字符串长度；
        ans[0]='\0',tmp[0]='\0',len=0;
        for(int i=0;i<m;i++)
            for(int j=0;j<60;j++)
                cin >> s[i][j];
        while(k<=60){   //字符串起点
            for(int i=0;i<=60-k;i++){    //枚举长度为k的字符串的起点
                memset(tmp,0,sizeof(tmp));//必须记得清空数组！！
                for(int j=i,t=0;j<i+k;j++)//这里的i+k，原来敲的是k，傻了傻了，还找了半天！！！
                    tmp[t++]=s[0][j];
                for(int j=1;j<m;j++){
                    if(strstr(s[j],tmp)==NULL){flag=1;break;}//不是公共子串就标记跳出；
                }
                if(flag==0){
                    if(k>len){strcpy(ans,tmp);len=k;}
                    else if(k==len&&strcmp(ans,tmp)>0){strcpy(ans,tmp);len=k;}
                }
                flag=0;
            }
            k++;
        }
        if(len!=0){
            for(int i=0;i<len;i++)
                cout << ans[i] ;
        }
        else
            cout << "no significant commonalities" ;
        cout << endl;
    }
    return 0;
}

2，KMP算法

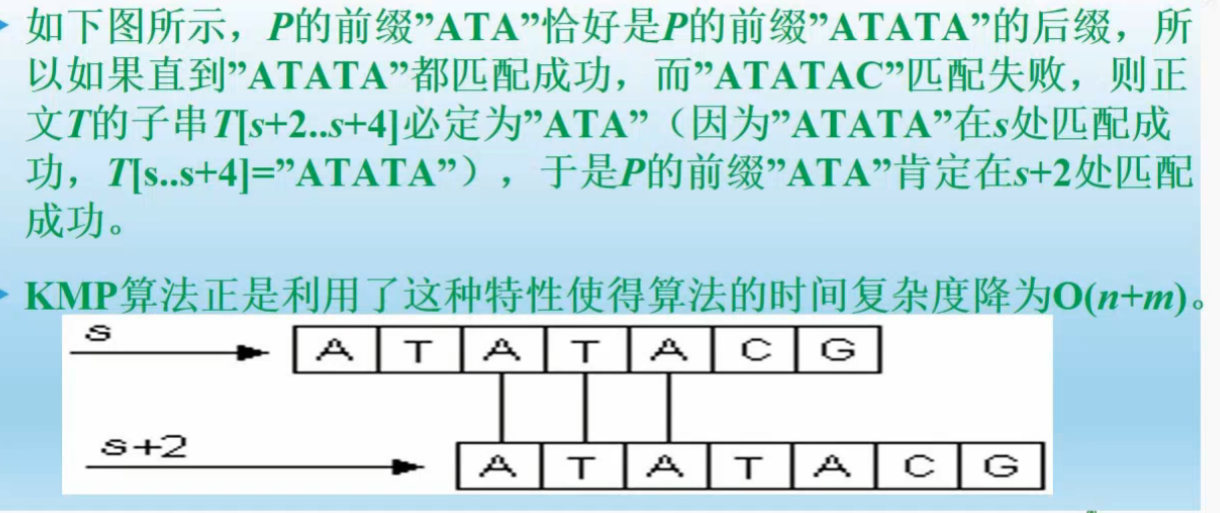
 例：POJ3461 Ouliop

 例：POJ3461　Oulipo

#include <iostream>
#include <cstdio>
#include <cstring>
const int maxn=10005;
using namespace std;
string s,t;
int n,m;
int nex[maxn];
void getnex(){
    int j=0,k=-1;
    nex[0]=-1;
    while(j<n){
        if(k==-1||t[j]==s[k]){
            nex[++j]=++k;
        }else
            k=nex[k];
    }
}
int kmp(){
    int i=0,j=0,cnt=0;
    getnex();
    while(i<m){
        if(j==-1||s[i]==t[j]){
            i++;j++;
        }else
            j=nex[j];
        if(j==n)
            cnt++;
    }
    return cnt;
}
int main()
{
    int c;
    //freopen("Atext.in","r",stdin);
    ios::sync_with_stdio(false);    //加了这个，关闭了输入输出同步就过了，不然超时；
    cin >> c;
    while(c--){
        int ans=0;
        cin >> t >> s;
        n=t.size();
        m=s.size();
        ans=kmp();
        cout << ans << endl;
    }
    return 0;
}