聚类--DBSCN

1、什么是DBSCN

DBSCAN也是一个非常有用的聚类算法。

• 它的主要优点:它不需要用户先验地设置簇的个数，可以划分具有复杂形状的簇，还可以找出不属于任何簇的点。
• DBSCAN比凝聚聚类和k均值稍慢，但仍可以扩展到相对较大的数据集。

1.1算法原理

DBSCAN的原理是识别特征空间的“拥挤”区域中的点，在这些区域中许多数据点靠近在一起。这些区域被称为特征空间中的密集区域。

• DBSCAN背后的思想：簇形成数据的密集区域，并由相对较空的区域分隔开。

在密集区域内的点被称为核心样本（或核心点），它们的定义如下。

• DBSCAN有两个参数：min_samples和eps。
  • 如果在距一个给定数据点eps的距离内至少有min_samples个数据点，那么这个数据点就是核心样本。
  • DBSCAN将彼此距离小于eps的核心样本放到同一个簇中。

一共有三种类型的点：核心点，与核心点的距离在eps之内的点（叫做边界点）和噪声。

• 如果DBSCAN算法在特定数据集上多次运行，那么核心点的聚类始终相同，同样的点也始终被标记为噪声。
  • 但边界点可能与不止一个簇的核心样本相邻。因此，边界点所属的簇依赖于数据点的访问顺序。
  • 一般来说只有很少的边界点，这种对访问顺序的轻度依赖并不重要。

2、应用于模拟数据make_blobs

  X, y = make_blobs(random_state=0,n_samples=12)

  dbscan = DBSCAN()

  clusters = dbscan.fit_predict(X)

  print("Cluster memberships:\n{}".format(clusters))

• 输出：

  Cluster memberships:
  [-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1]
  

因为eps和min_samples设置不当，所有的数据都被标记为噪声

• 可视化

  mglearn.plots.plot_dbscan()
  

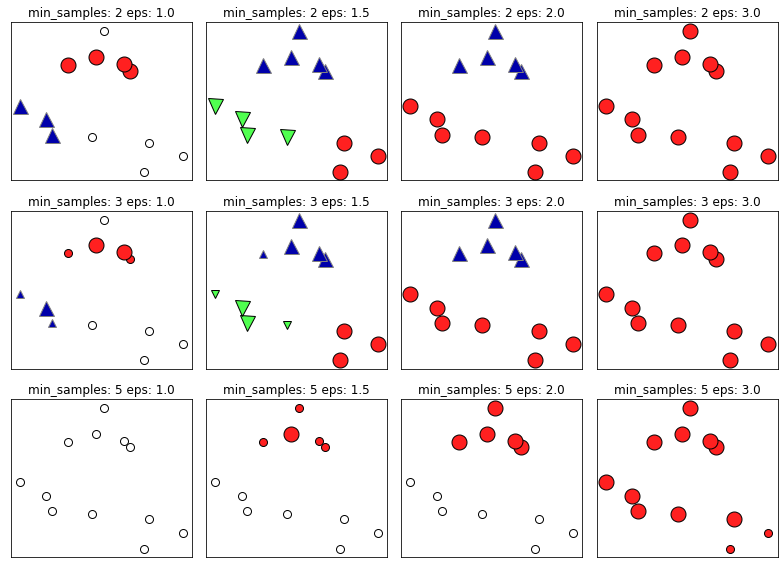
• 在这张图中，属于簇的点是实心的，噪声点为空心。核心样本显示为较大的标记，边界点则显示为较小的标记。
  • 增大eps，扩大核心点的领域，会让一个簇变得更大
  • 增大min_samples会让一个簇中包含更多的点，同时核心点变小，噪声变多

• eps更重要
  • 它决定了点与点之间“接近的含义”。
    • eps过小，没有点是核心样本
    • eps过大，所有点成单个簇
• min_samples是为了判断稀疏区域内的点被标记为异常值还是形成自己的簇
  • 决定了簇的尺寸

3、应用于模拟数据make_moons

虽然DBSCAN不需要显式地设置簇的个数，但设置eps可以隐式地控制找到的簇的个数。使用StandardScaler或MinMaxScaler对数据进行缩放之后，有时会更容易找到eps的较好取值，因为使用这些缩放技术将确保所有特征具有相似的范围.

  from sklearn.datasets import make_moons
  from sklearn.preprocessing import StandardScaler
  from matplotlib import pyplot as plt

  X, y = make_moons(n_samples=200,noise=0.05,random_state=0)

  #将数据缩放成平均值为0，方差为1
  scaler = StandardScaler().fit(X)
  X_scaled = scaler.transform(X)

  dbscan = DBSCAN()
  clusters = dbscan.fit_predict(X_scaled)

  #绘制簇分配

  plt.scatter(X_scaled[:,0],X_scaled[:,1],c=clusters,cmap=mglearn.cm2,s=60)

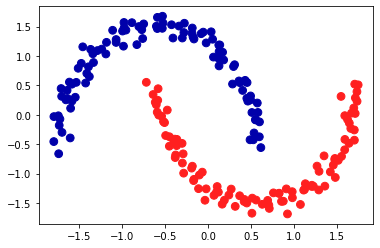
可以看到，利用DBSCAN的默认设置，算法找到了两个半圆形并将其分开。

由于算法找到了我们想要的簇的个数（2个），因此参数设置的效果很好。

• 如果将eps减小到0.2（默认值为0.5），我们将会得到8个簇，这显然太多了。
• 将eps增大到0.7则会导致只有一个簇。

4、参考文献

《python机器学习基础教程》P143-P147