Python数据分析--Numpy常用函数介绍(4)--Numpy中的线性关系和数据修剪压缩

摘要：总结股票均线计算原理--线性关系，也是以后大数据处理的基础之一，NumPy的 linalg 包是专门用于线性代数计算的。作一个假设，就是一个价格可以根据N个之前的价格利用线性模型计算得出。

前一篇，在计算均线，指数均线时，分别计算了不同的权重，比如

和

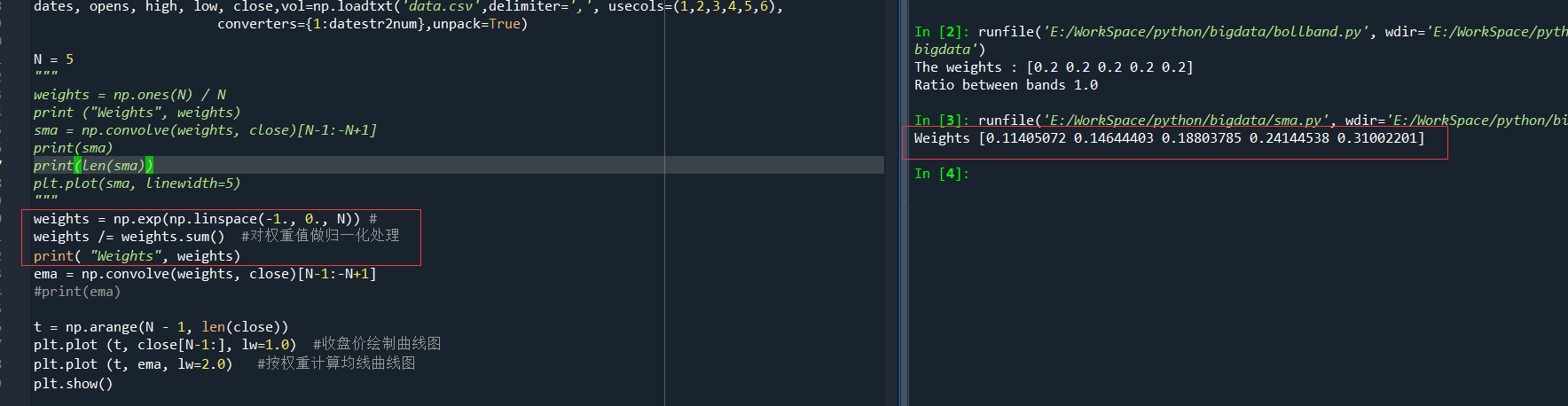
都是按不同的计算方法来计算出相关的权重，一个股价可以用之前股价的线性组合表示出来，也即，这个股价等于之前的股价与各自的系数相乘后再做加和的结果，但是，这些系数是需要我们来确定的，也即一个线性相关的权重。
一、用线性模型预测价格
创建步骤如下：
1）先获取一个包含N个收盘价的向量（数组）：

N=10
#N=len(close)
new_close = close[-N:]
new_closes= new_close[::-1]
print (new_closes)

运行结果：[39.96 38.03 38.5  38.6  36.89 37.15 36.61 37.21 36.98 36.47]

2)初始化一个N×N的二维数组 A ，元素全部为 0

A = np.zeros((N, N), float)
print ("Zeros N by N", A)

3）用数组new_closes的股价填充数组A

for i in range(N):
    A[i,] = close[-N-i-1: -1-i]
print( "A", A)

试一下运行结果，并观察填充后的数组A

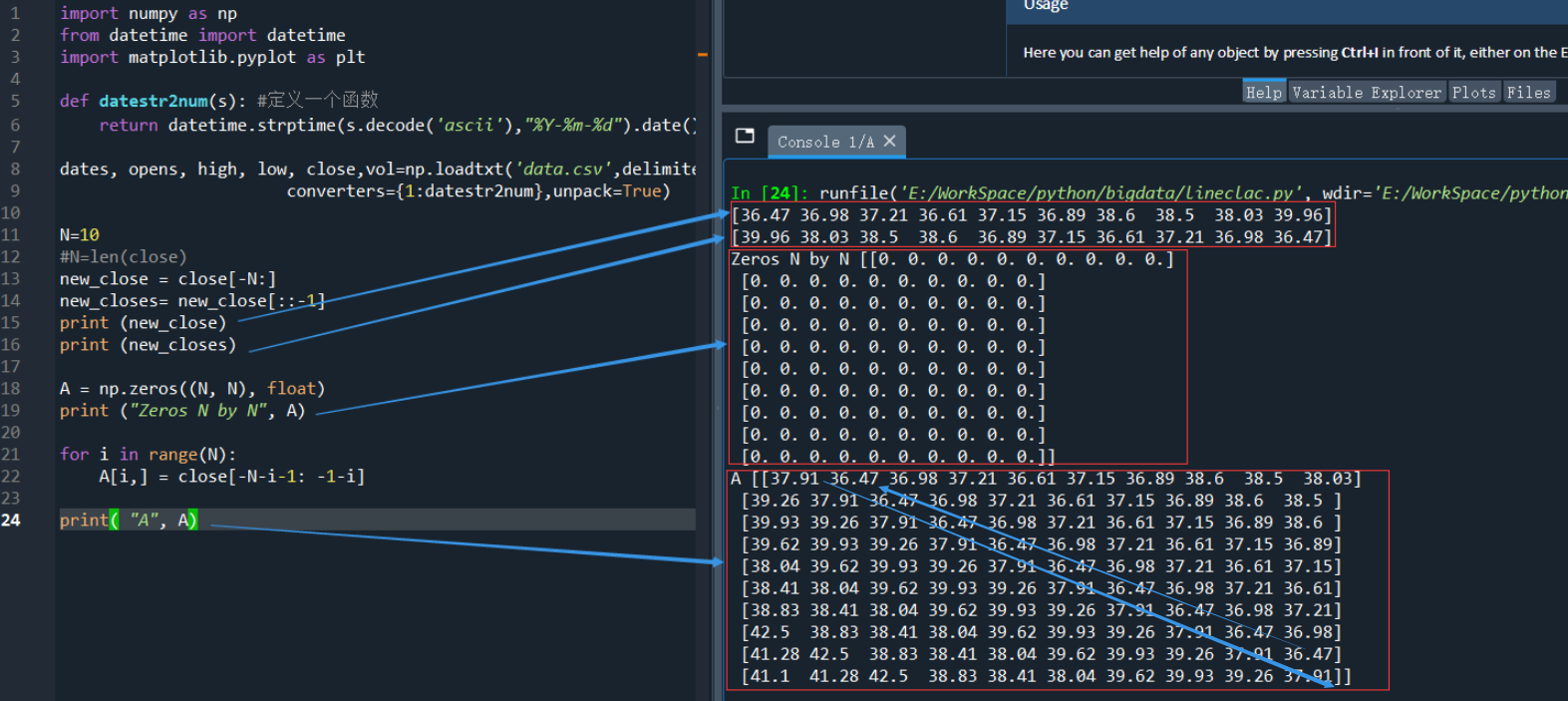
4）选取合适的权重

Weights [0.11405072 0.14644403 0.18803785 0.24144538 0.31002201]和The weights : [0.2 0.2 0.2 0.2 0.2]哪一种权重更合理？用线性代数的术语来说，就是解一个最小二乘法的问题。

要确定线性模型中的权重系数，就是解决最小平方和的问题，可以使用 linalg包中的 lstsq 函数来完成这个任务

(x, residuals, rank, s) = np.linalg.lstsq(A,new_closes)

其中，x是由A,new_closes通过np.linalg.lstsq（）函数，即生成的权重（向量），residuals为残差数组、rank为A的秩、s为A的奇异值。

5)预测股价，用NumPy中的 dot()函数计算系数向量与最近N个价格构成的向量的点积（dot product）,这个点积就是向量new_closes中价格的线性组合，系数由向量 x 提供

print( np.dot(new_closes, x))

完整代码如下：

import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt

def datestr2num(s): #定义一个函数
    return datetime.strptime(s.decode('ascii'),"%Y-%m-%d").date().weekday()

dates, opens, high, low, close,vol=np.loadtxt('data.csv',delimiter=',', usecols=(1,2,3,4,5,6),
                       converters={1:datestr2num},unpack=True)

N=10
#N=len(close)
new_close = close[-N:]
new_closes= new_close[::-1]

A = np.zeros((N, N), float)

for i in range(N):
    A[i,] = close[-N-i-1: -1-i]

print( "A", A)

(x, residuals, rank, s) = np.linalg.lstsq(A,new_closes)
print(x) #权重系数向量 

print('\n')
print(residuals)  #残差数组
print('\n')
print(rank) #A的秩
print(s)
print('\n')#奇异值
print( np.dot(new_closes, x))

运行结果如下：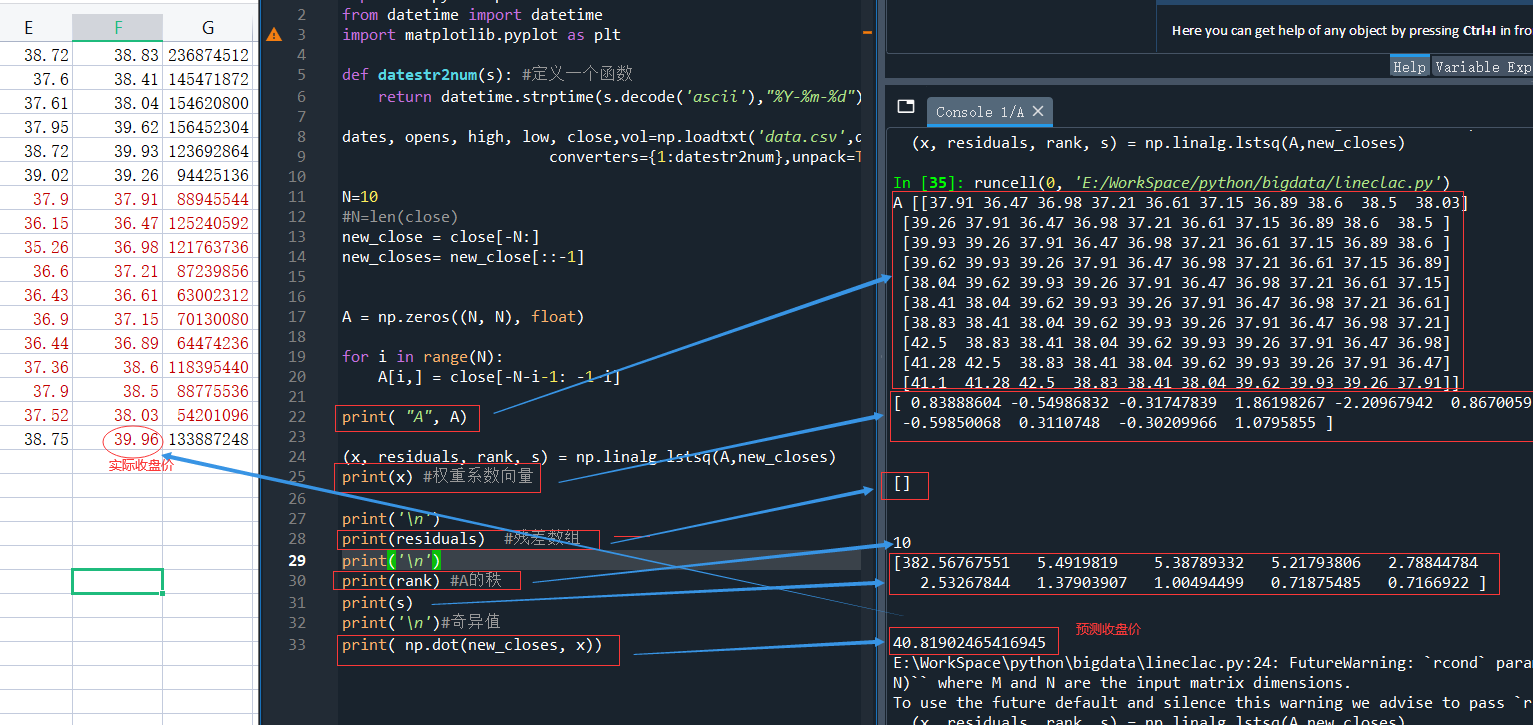

二、趋势线

趋势线，是根据股价走势图上很多所谓的枢轴点绘成的曲线。描绘价格变化的趋势。可以让计算机来用非常简易的方法来绘制趋势线

(1) 确定枢轴点的位置。假定枢轴点位置 为最高价、最低价和收盘价的算术平均值。pivots = (high + low + close ) / 3

从枢轴点出发，可以推导出股价所谓的阻力位和支撑位。阻力位是指股价上升时遇到阻力，在转跌前的最高价格；支撑位是指股价下跌时遇到支撑，在反弹前的最低价格（阻力位和支撑位并非客观存在，它们只是一个估计量）。基于这些估计量，就可以绘制出阻力位和支撑位的趋势线。我们定义当日股价区间为最高价与最低价之差

(2) 定义一个函数用直线 y= at + b 来拟合数据，该函数应返回系数 a 和 b，再次用到 linalg 包中的 lstsq 函数。将直线方程重写为 y = Ax 的形式，其中 A = [t 1] ， x = [a b] 。使用 ones_like 和 vstack 函数来构造数组 A

numpy.ones_like(a, dtype=None, order='K', subok=True) 返回与指定数组具有相同形状和数据类型的数组，并且数组中的值都为1。

numpy.vstack(tup)     [source]  垂直(行)按顺序堆叠数组。  这等效于形状(N,)的1-D数组已重塑为(1,N)后沿第一轴进行concatenation。 重建除以vsplit的数组。如下两小例：

>>> a = np.array([1, 2, 3]) 
>>> b = np.array([2, 3, 4]) 
>>> np.vstack((a,b)) 
array([[1, 2, 3],        
       [2, 3, 4]])

>>> a = np.array([[1], [2], [3]])
>>> b = np.array([[2], [3], [4]])
>>> np.vstack((a,b))
array([[1],
       [2],
       [3],
       [2],
       [3],
       [4]])    

完整代码如下：

import numpy as np
from datetime import datetime
import matplotlib.pyplot as plt

def datestr2num(s): #定义一个函数
    return datetime.strptime(s.decode('ascii'),"%Y-%m-%d").date().weekday()

dates, opens, high, low, close,vol=np.loadtxt('data.csv',delimiter=',', usecols=(1,2,3,4,5,6),
                       converters={1:datestr2num},unpack=True)
"""
N=10
#N=len(close)
new_close = close[-N:]
new_closes= new_close[::-1]

A = np.zeros((N, N), float)

for i in range(N):
    A[i,] = close[-N-i-1: -1-i]

print( "A", A)
(x, residuals, rank, s) = np.linalg.lstsq(A,new_closes)
print(x) #权重系数向量
print(residuals)  #残差数组
print(rank) #A的秩
print(s)
print( np.dot(new_closes, x))
"""
pivots = (high + low + close ) / 3

def fit_line(t, y):
    A = np.vstack([t, np.ones_like(t)]).T
# np.ones_like(t) 即定义一个像t一样，有相同形状和数据类型的数组，并且数组中的值都为1
    return np.linalg.lstsq(A, y)[0]

t = np.arange(len( close)) #按close数列创建一个数列t

sa, sb = fit_line(t, pivots - (high - low)) #用直线y=at+b来拟合数据，该函数应返回系数a(sa) 和 b(sb)
ra, rb = fit_line(t, pivots + (high - low))
support = sa * t + sb     #计算支撑线数列
resistance = ra * t + rb  #计算阻力线数列

condition = (close > support) & (close < resistance)#设置一个判断数据点是否位于趋势线之间的条件，作为 where 函数的参数
between_bands = np.where(condition)

plt.plot(t, close,color='r')
plt.plot(t, support,color='g')
plt.plot(t, resistance,color='y')
plt.show()

运行结果：

三、数组的修剪和压缩

NumPy中的 ndarray 类定义了许多方法，可以对象上直接调用。通常情况下，这些方法会返回一个数组。

ndarray 对象的方法相当多，像前面遇到的 var 、 sum 、 std 、 argmax 、argmin 以及 mean 函数也均为 ndarray 方法。下面介绍一下数组的修前与压缩。

1、  clip 方法返回一个修剪过的数组：将所有比给定最大值还大的元素全部设为给定的最大值，而所有比给定最小值还小的元素全部设为给定的最小值

a = np.arange(10)
print("a =", a)
print("Clipped", a.clip(3, 7))

运行结果：

a = [0 1 2 3 4 5 6 7 8 9]
Clipped [3 3 3 3 4 5 6 7 7 7]

很明显，a.clip(3,7)将数组a中的小于3的设置为3，大于7的全部设置为7.

2、 compress 方法返回一个根据给定条件筛选后的数组

b = np.arange(10)
print (a)
print ("Compressed", a.compress(a >3))

运行结果：

[0 1 2 3 4 5 6 7 8 9]
Compressed [4 5 6 7 8 9]

四、阶乘

prod() 方法，可以计算数组中所有元素的乘积.

c = np.arange(1,5)
print("b =", c)
print("Factorial", c.prod())

运行结果：

b = [1 2 3 4]
Factorial 24

如果想知道1~8的所有阶乘值，调用 cumprod()方法，计算数组元素的累积乘积。

print( "Factorials", c.cumprod())

运行结果：

Factorials [  1   2   6  24 120]

本篇主要介绍了一个通过现在有数据，用函数 y= at + b 来拟合数据进行线性拟合后，用 linalg包中的 lstsq 函数来完成最小二乘相关后，预测股价的实例，来了解了一些numpy的函数及作用；同时介绍 了数据修剪及压缩和阶乘的计算。