怎么理解超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n)
怎么理解超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n)
前言:重在记录,可能出错。
超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n),也就是: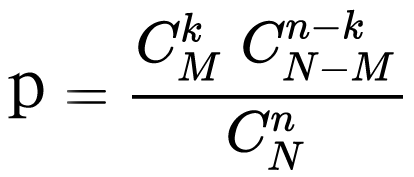
到底要怎么理解呢?
举个例子:
设有N件产品,其中有M件次品,现在从中任取n件,问其中恰有k(k≤M)件次品的概率是多少?
思考:
设N件产品中任取n件为事件A,则事件A共包含 个基本事件。
个基本事件。
设恰好取出k个次品为事件B,此k个次品共有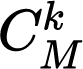 种取法,也就是在M个次品中取k个。接下来,每一种取法对应着需要取出n-k个正品,同理在N-M个正品中取n-k个,有
种取法,也就是在M个次品中取k个。接下来,每一种取法对应着需要取出n-k个正品,同理在N-M个正品中取n-k个,有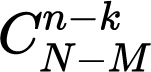 种取法。
种取法。
因此事件B共包含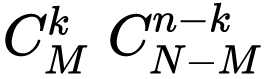 个基本事件。
个基本事件。
根据古典概型的计算方法:P(B)=B事件包含的基本事件数/样本空间中基本事件的总数,因此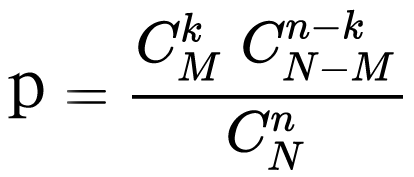
怎么理解超几何分布概率公式:p=C(M,k)C(N-M,n-k)/C(N,n)的更多相关文章
- uva-11021-全概率公式
https://vjudge.net/problem/UVA-11021 有n个球,每只的存活期都是1天,他死之后有pi的概率产生i个球(0<=i<n),一开始有k个球,问m天之后所有球都 ...
- hdu 4762 Cut the Cake概率公式
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=4762 题目大意:一个圆形蛋糕,现在要分成M个相同的扇形,有n个草莓,求n个草莓都在同一个扇形上的概率. ...
- HDU 4326Game(比较难理解的概率dp)
Game Time Limit: 10000/5000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Subm ...
- Chapter 1: 随机事件及其概率
1. 随机试验,样本点,样本空间 若试验具有下列特点: 在相同条件下可重复进行 每次试验的可能结果不止一个,且所有可能结果在实验前是已知的 实验前不能确定哪一个结果会发生 则称该试验为随机试验,常记为 ...
- Hash中的一些概率计算
Hash是把锋利的刀子,处理海量数据时经常用到,大家可能经常用hash,但hash的有些特点你是否想过.理解过.我们可以利用我们掌握的概率和期望的知识,来分析Hash中一些有趣的问题,比如: 平均每个 ...
- ACM - 概率、期望题目 小结(临时)
概率DP求期望大多数都是全期望公式的运用.主要思考状态空间的划分以及状态事件发生的概率.问题可以分为无环和有环两类.无环一类多数比较简单,可以通过迭代或者记忆化搜索完成.有环一类略复杂,可以通过假设方 ...
- poj 2096 Collecting Bugs (概率dp 天数期望)
题目链接 题意: 一个人受雇于某公司要找出某个软件的bugs和subcomponents,这个软件一共有n个bugs和s个subcomponents,每次他都能同时随机发现1个bug和1个subcom ...
- 《A First Course in Probability》-chaper3-条件概率和独立性-贝叶斯公式、全概率公式
设有事件A.B. 下面结合具体的题目进一步理解这种方法: Q1:保险公司认为人可以分为两类,一类易出事故,另一类则不易出事故.统计表明,一个易出事故者在一年内发生事故的概率是0.4,而对不易出事故者来 ...
- 对Kalman(卡尔曼)滤波器的理解
1.简单介绍(Brief Introduction) 在学习卡尔曼滤波器之前,首先看看为什么叫"卡尔曼". 跟其它著名的理论(比如傅立叶变换.泰勒级数等等)一样.卡尔曼也是一个人的 ...
- MLAPP——概率机器学习知识汇总
<机器学习>课程使用Kevin P. Murphy图书<Machine Learning A Probabilistic Perspective>本英语教材,本书从一个独特的数 ...
随机推荐
- 最全面 think php 实现微信公众号回复编号进行投票,自定义菜单功能
前期准备工作 https://developers.weixin.qq.com/doc/offiaccount/Message_Management/Receiving_standard_messag ...
- codeforce F. Multicolored Markers
http://codeforces.com/contest/1029/problem/F 这道题真的一点都不难-------------------- 对于大矩形面积a+b,从差距最小的因数开始遍历, ...
- FTP传大文件又慢又麻烦,有没有更好的替代传输方案?
FTP作为常见的文件传输协议已经具有很长的历史,最早可以追溯到上世纪70年代.至今FTP仍然较为活跃,然而许多企业已经开始不满足于FTP的功能局限性,开始另外寻找合适的文件传输产品. 目前数据正在爆炸 ...
- JAVA丑数
leetcode题目链接 有些数的素因子只有 3,5,7,请设计一个算法找出第 k 个数.注意,不是必须有这些素因子,而是必须不包含其他的素因子.例如,前几个数按顺序应该是 1,3,5,7,9,15, ...
- react项目打包后点击index.html页面出现空白
当本地打包后的文件,直接通过文件路径访问,出现空白或者,提示打包后的build内的js,css文件路径错误,有以下两种方式 方式一(无网络限制的情况下使用): 1.全局安装serve启动本地服务: n ...
- redis底层数据结构之压缩列表(ziplist)
压缩列表(ziplist) 压缩列表(ziplist)是redis 为了节约内存而开发的,由连续内存块组成的顺序型数据结构,适用于长度较小的值 存取的效率高,内存占用小,但由于内存是连续的,在修改的时 ...
- Document.createEvent与new Event区别
Document.createEvent 写法: const e = document.createEvent('HTMLEvents'); e.initEvent('click', true, tr ...
- Unity一键制作预制体Prefab一键修改Prefab属性
1.适用于制作多个预制体(一个模型文件下面几百个子物体,都需要制作成预制体,这一个一个拖不是要炸裂) 模型资源如下图 2.模型先放到Resources文件夹下面方便读取,制作完预制体可以给他拖到其他文 ...
- kubeshpere 相关配置
1.配置maven镜像仓库 1.1.查找ks-devops-agent 平台管理 -> 集群管理 -> 配置中心 -> 配置 -> 检索 ks-devops-agent 1.2 ...
- 添加matlab到右键菜单并从当前目录打开
前言 因为每次打开matlab都得切换一下工作目录,由于目录不固定,所以感觉会很麻烦,所以就想着怎么添加matlab到右键菜单,并从指定目录打开,不过网上没有关于怎么设置这个的,不过却又很多设置cm ...
