数论专项复习（一）扩展欧几里得算法(exgcd)

简介

扩展欧几里得算法（简称扩欧，exgcd），用来求下列方程的一组解：

\[ax+by=(a,b)
\]

算法介绍

1. 裴蜀定理

裴蜀定理（Bézout's lemma）：若 $a\in \mathbb{Z},b \in \mathbb{Z}$ 且 $a,b$ 不全为 $0$，则关于 $x,y$ 的方程 $ax+by=(a,b)$ 一定有整数解。

证明：略（其实是不会）

2. 欧几里得定理

欧几里得定理：$(a,b)=(b,a \bmod b)$。

证明：略（其实还是不会）

用途：著名的辗转相除法就是用欧几里得定理证明的。

3. Exgcd

伪代码：

Integer X,Y // The Solution of AX+BY=(A,B)

Exgcd(Integer A,Integer B)

	If B equals 0

		X = 1

		Y = 0

		Return

	Else

		Exgcd(B,A mod B)

		X = X - A / B * Y

		Swap X,Y

End

证明：

当 $b=0$ 时，显然有 $x=1,y=0$，使得 $xa+yb=(a,b)$。
当 $b>0$，则 $(b,a \bmod b)$。存在整数 $x,y$，满足 $bx+(a\bmod b)y=(b,a\bmod b)$。
令 $x'=y,y'=x-\lfloor\dfrac{a}{b}\rfloor y$，$ax'+by'=(a,b)$。

代码：

int x,y;

void exgcd(int a,int b){

	if(b==0){

		x=1;

		y=0;

	}

	else{

		exgcd(b,a%b);

		int tmp=x;

		x=y;

		y=tmp-a/b*y;

	}

}

时间复杂度 $O(\log n)$。

例题

CF510D Fox And Jumping

给出 $n$ 张卡片，分别有 $l_i$ 和 $c_i$。在一条无限长的纸带上，你可以选择花 $c_i$ 的钱来购买卡片 $i$，从此以后可以向左或向右跳 $l_i$ 个单位。问你至少花多少元钱才能够跳到纸带上全部位置。若不可能，输出 $-1$。

$1 \leq n \leq 300,1 \leq l_i \leq 10^{9},1 \leq c_i \leq 10^{5}$

首先，如果我们可以选出一些个卡片 $(l_i,c_i)$，使得全部的 $c_i$ 互质（我的意思是 $(c_i,(c_{i+1},(c_{i+2},\cdots))) = 1$ ）。因为裴蜀定理 $c_ix+c_jy=1$ 有解，所以一定可以从位置 $x$ 跳到 $x \pm 1$。

一开始，我的思路是能选择 $c = 1$ 就选择，否则选择两个不同的。Hack 数据：

7

15015 10010 6006 4290 2730 2310 1

1 1 1 1 1 1 10

答案应该是 $6$（选择前 $6$ 个）。

然后我们考虑 DP，设 $f_{i,j}$ 为选择前 $i$ 个，选择的数的 $\gcd$ 是 $j$ 的最小代价。显然，最后答案是 $f_{n,1}$。动态转移方程：

\[f_{i,(j,l_i)} = \left\{
\begin{aligned}
& \min(f_{i,(j,l_i)},f_{i-1,j} + c_i) & (j \neq l_i) \\
& \min(f_{i-1,(j,l_i)},c_i) & (j = l_i)
\end{aligned}
\right.
\]

无法通过本题，考虑优化。发现这个动态转移方程很像三角形不等式 $\operatorname{dis}_{u}=\min(\operatorname{dis}_{u},\operatorname{dis}_{v}+W_{u,v})$，想到用最短路优化。

使用堆优化 Dijkstra 算法可以做到 $O(n^{3})$，可以通过本题。

#include <bits/stdc++.h>

#define int long long

#define gcd __gcd

using namespace std;

unordered_map<int, int> dis;

unordered_set<int> vis;

priority_queue<pair<int,int>, vector<pair<int,int> >, greater<pair<int,int> > > pq;

int n,l[305],c[305];

void dijkstra(){

	pq.push({0,0});

	dis[0]=0;

	while(!pq.empty()){

		int x = pq.top().second;

		pq.pop();

		if(x==1){

			break;

		}

		if(vis.find(x) != vis.end()){

			continue;

		}

		vis.insert(x);

		for(int j=1;j<=n;j++){

			int y = gcd(x,l[j]);

			if(dis.find(y) == dis.end()){

				dis[y] = INT_MAX;

			}

			if(dis[y]>dis[x]+c[j]){

				dis[y]=dis[x]+c[j];

				pq.push(make_pair(dis[y],y));

			}

		}

	}

}

signed main(){

	ios::sync_with_stdio(false);

	cin.tie(0);cout.tie(0);

	cin>>n;

	for(int i=1;i<=n;i++){

		cin>>l[i];

	}

	for(int j=1;j<=n;j++){

		cin>>c[j];

	}

	dijkstra();

	if(dis.find(1)==dis.end()){

		// Impossible

		cout<<-1;

	}

	else{

		cout<<dis[1];

	}

	return 0;

}

AC Record

UVA10104 Euclid Problem

多组数据。每组数据给出两个正整数 $A,B$。令 $D = (A,B)$，求出关于 $x,y$ 的方程 $Ax+By=D$ 中 $|x|+|y|$ 最小的整数解。输出 $x,y,D$。

$1 \leq A,B \leq 10^{9}$

Exgcd 的模板题。

代码：

#include <bits/stdc++.h>

#define int long long

using namespace std;

int x,y;

void exgcd(int a,int b){

	if(b==0){

		x=1;

		y=0;

	}

	else{

		exgcd(b,a%b);

		int tmp=x;

		x=y;

		y=tmp-a/b*y;

	}

}

signed main(){

	int a,b;

	while(cin>>a>>b){

		exgcd(a,b);

		cout<<x<<' '<<y<<' '<<__gcd(a,b)<<'\n';

	}

	return 0;

}

AC Record

P1082 [NOIP2012 提高组] 同余方程

求关于 $x$ 的同余方程 $ax\equiv 1\pmod{b}$ 的最小正整数解。数据保证有解。（即，$a$ 在模 $b$ 意义下的最小逆元）

$2 \leq a,b \leq 2 \times 10^{9}$

互质的数才有逆元，所以 $(a,b)=1$。

发现其实就是求 $ax \equiv (a,b) \pmod{b}$，两边同时加上 $by$，得到 $ax+by\equiv (a,b) \pmod{b}$。我们先用 exgcd 求 $ax+by=(a,b)$ 中的 $x$，然后直接求出 $x \bmod b$ 即可。

代码：

#include <iostream>

#define int long long

using namespace std;

int x,y;

void exgcd(int a,int b){

	if(b==0){

		x=1;

		y=0;

	}

	else{

		exgcd(b,a%b);

		int tmp=x;

		x=y;

		y=tmp-a/b*y;

	}

}

signed main(){

	int a,b;

	cin>>a>>b;

	exgcd(a,b);

	cout<<(x%b+b)%b;

	return 0;

}

P2613 【模板】有理数取余

给出一个有理数 $c=\frac{a}{b}$，求 $c \bmod 19260817$ 的值。如果无解，输出 Angry!。

对于所有数据，保证 $0\leq a \leq 10^{10001}$，$1 \leq b \leq 10^{10001}$，且 $a, b$ 不同时是 $19260817$ 的倍数。

显然，若 $b=0$，则无解。否则有解。

\[\begin{aligned}
& \frac{a}{b} \pmod{19260817} \\
& = a \times b^{-1} \pmod{19260817}
\end{aligned}
\]

怎么求逆元，上一题已经告诉大家了。最后注意读入，读入的时候顺便取余以免高精。这样子是正确的（因为同余两边同时模一个与同余式两边互质的数，同余依然成立）

代码：

#include <bits/stdc++.h>

#define int long long

using namespace std;

int x,y;

const int MOD = 19260817;

int a,b;

inline int read() {

	int res = 0, ch = getchar();

	while(!isdigit(ch) and ch != EOF){

		ch = getchar();

	}

	while(isdigit(ch)) {

		res = (res << 3) + (res << 1) + (ch - '0');

		res %= MOD;

		ch = getchar();

	}

	return res;

}

void exgcd(int a,int b) {

	if(b==0) {

		x=1;

		y=0;

	} else {

		exgcd(b,a%b);

		int tmp=x;

		x=y;

		y=tmp-a/b*y;

	}

}

signed main() {

	a=read(),b=read();

	if(b==0) {

		printf("Angry!");

		return 0;

	}

	exgcd(b,MOD);

	x=(x+MOD)%MOD;

	cout<<a*x%MOD<<endl;

	return 0;

}

AC Record

P5656 【模板】二元一次不定方程 (exgcd)

$T$ 组数据，每组数据：

给定不定方程 $ax+by=c$。

若该方程无整数解，输出 $-1$。

若该方程有整数解，且有正整数解，则输出其正整数解的数量，所有正整数解中 $x$ 的最小值，所有正整数解中 $y$ 的最小值，所有正整数解中 $x$ 的最大值，以及所有正整数解中 $y$ 的最大值。

若方程有整数解，但没有正整数解，你需要输出所有整数解中 $x$ 的最小正整数值， $y$ 的最小正整数值。

正整数解即为 $x, y$ 均为正整数的解，$\boldsymbol{0}$ 不是正整数。

整数解即为 $x,y$ 均为整数的解。

$x$ 的最小正整数值即所有 $x$ 为正整数的整数解中 $x$ 的最小值，$y$ 同理。

对于 $100\%$ 的数据，$1 \le T \le 2 \times {10}^5$，$1 \le a, b, c \le {10}^9$。

首先，若 $(a,b) \not\mid c$，则该方程无解。
当 $x$ 变为最小正整数解时，$y$ 最大，若 $y<0$，则没有正整数解。
当 $y$ 变为最小正整数解时，$x$ 最大，若 $x<0$，则没有正整数解。
此外有解。

代码：

#include <bits/stdc++.h>

#define int long long

using namespace std;

int t,a,b,c,x,y;

void exgcd(int a,int b){

	if(b==0){

		x=1,y=0;

		return;

	}

	else{

		exgcd(b,a%b);

		int tmp=x;

		x=y;

		y=tmp-y*(a/b);

	}

}

signed main(){

	cin>>t;

	while(t--){

		cin>>a>>b>>c;

		if(c%__gcd(a,b) != 0){

			cout<<-1<<'\n';

		}

		else{

			int d = __gcd(a,b);

			a/=d;b/=d;c/=d;

			exgcd(a,b);

			x*=c;y*=c;

			if(x<=0){

				int t=-x/b+1;

				x=x%b+b;

				y=y-t*a;

				if(y<=0){

					cout<<x<<' '<<((y%a)+a)<<'\n';

					continue;

				}

			}

			if(y<=0){

				int t=-y/a+1;

				y=y%a+a;

				x=x-t*b;

				if(x<=0){

					cout<<((x%b)+b)<<' '<<y<<'\n';

					continue;

				}

			}

			int t=x/b;

			x%=b;

			if(x==0){

				x=x+b;

				--t;

			}

			y+=t*a;

			int minx=x,maxy=y;

			t=y/a;y%=a;

			if(y==0){

				y+=a;

				t--;

			}

			x+=t*b;

			cout<<((x-minx)/b+1)<<' ';

			cout<<minx<<' ';

			cout<<y<<' ';

			cout<<x<<' ';

			cout<<maxy<<'\n';

		}

	}

	return 0;

}

P2054 [AHOI2005] 洗牌

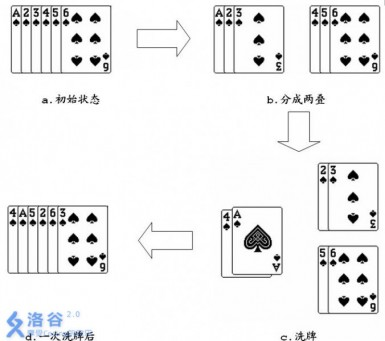
对于扑克牌的一次洗牌是这样定义的，将一叠 $N$（ $N$ 为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。

如果对一叠 $6$ 张的扑克牌 1 2 3 4 5 6，进行一次洗牌的过程如下图所示：

从图中可以看出经过一次洗牌，序列 1 2 3 4 5 6 变为 4 1 5 2 6 3。当然，再对得到的序列进行一次洗牌，又会变为 2 4 6 1 3 5。

如果给定长度为 $N$ 的一叠扑克牌，并且牌面大小从 $1$ 开始连续增加到 $N$（不考虑花色），对这样的一叠扑克牌，进行 $M$ 次洗牌。求经过洗牌后的扑克牌序列中第 $L$ 张扑克牌的牌面大小。

$0＜N≤10^{10},0≤M≤10^{10}$，且 $N$ 为偶数。

对于一张原来在 $n$ 的牌，他现在的位置 $L$：

\[n \times 2^{M} \equiv L \pmod{n+1}
\]

现在反推 $n$：

\[n \equiv L \times (2^{M})^{-1} \pmod{n+1}
\]

用 exgcd 求出 $2^{M}$ 的逆元，然后直接算。需要龟速乘、快速幂和 __int128。

代码：

#include <bits/stdc++.h>

#define int __int128

using namespace std;

int n,m,l,x,y;

inline int read()

{

	int x=0,f=1;char ch=getchar();

	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}

	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}

	return x*f;

}

void exgcd(int a,int b){

	if(b==0){

		x=1,y=0;

		return;

	}

	else{

		exgcd(b,a%b);

		int tmp=x;

		x=y;

		y=tmp-y*(a/b);

	}

}

int pow(int a,int b,int mod) {

	int ans=1;

	for(; b; b>>=1,a=a*a%mod) {

		if(b&1) {

			ans=ans*a%mod;

		}

	}

	return ans;

}

int mul(int a,int b,int mod) {

	int ans=0;

	for(; b; b>>=1,a=(a+a)%mod) {

		if(b&1) {

			ans=(ans+a)%mod;

		}

	}

	return ans;

}

signed main(){

	n=read();m=read();l=read();

	exgcd(pow(2,m,n+1),n+1);

	x=(x%(n+1)+(n+1))%(n+1);

	cout<<(long long)(mul(x,l,n+1))<<'\n';

	return 0;

}

AC Record