方差分析2——双因素方差分析（R语言）

双因素方差分析（Double factor variance analysis) 有两种类型：一个是无交互作用的双因素方差分析，它假定因素A和因素B的效应之间是相互独立的，不存在相互关系；另一个是有交互作用的双因素方差分析，它假定因素A和因素B的结合会产生出一种新的效应。例如，若假定不同地区的消费者对某种品牌有与其他地区消费者不同的特殊偏爱，这就是两个因素结合后产生的新效应，属于有交互作用的背景；否则，就是无交互作用的背景。这里介绍无交互作用的双因素方差分析。

一、双因素方差分析

当方差分析涉及两个分类试验因素对试验指标的影响差异性时，则可称为双因素方差分析。如要检验不用地区的不同品牌商品的市场销售潜力是否相等，或要检验不同区域不同品牌连锁店的服务消费者认可度是否相等，两个例子中均涉及“区域”、“品牌”两个因素，故其属于双因素方差分析。

1.1问题描述

在双因素分析中，所考虑的因素有两个，各因素又包含若干种水平，而不同水平之间有可能存在系统性差异，只是需要通过检验才能验证这种系统差异是否确实存在。在检验过程中，需要分析两种因素下的不同水平间的差异是否显著存在。

例1 设有 n 个工人使用 m 台机器生产同一种产品，记录每个工人使用每台机器的日产量。那么不同工人之间的生产能力是否有差异，不同机器之间的生产性能是否有差异，需要进行检验，这里所要分析的因素既包括“工人”，也包括“机器”。

例2 灯泡厂在 3 个不同技术员操作下，用 4 种不同配料方案制成的灯丝生产了 4 批灯泡，那么不同技术员之间的技术是否有差异，不同配料方案之间的性能是否有差异，需要进行检验，这里所要分析的因素既包括“技术员”，也包括“配料方案”。

为分析需要，在双因素方差分析中，用A表示因素1，用B表示因素2，A因素的k个水平（总体）分别用A1,A2,…,Ak表示，B 因素的 r 个水平（总体）分别用B1,B2,…,Br表示，每个观测值用 xij(i =1,2,…,k; j =1,2,…,r )表示，即 xij表示 A 因素第 i 个水平（总体）和 B 因素第j个水平所组合成的k×r个总体中抽取的样本量为1的样本观测值。

1.2 分析步骤

第一步，提出假设

对A因素提出的假设为

H0：μ1=μ2=…=μk(假设A因素各水平间没有显著差异，也即A因素对试验指标无显著影响)

H1：μi不全相等（i=1,2,…,k）（假设A因素各水平间有显著差异，也即A因素对试验指标有显著影响）

对B因素提出的假设为

H0：μ1=μ2=…=μr(假设B因素各水平间没有显著差异，也即B因素对试验指标无显著影响)

H1：μi不全相等（i=1,2,…,r）(假设B因素各水平间有显著差异，也即B因素对试验指标有显著影响）

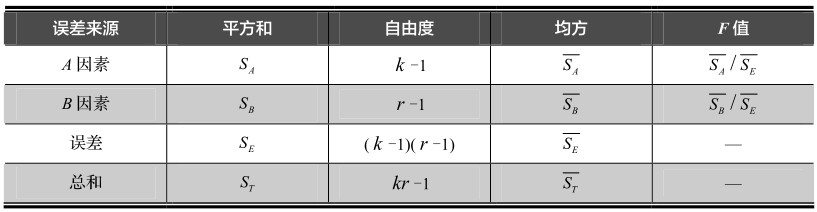
第二步，构造方差分析表

双因素的方差分析表如下表所示：

二、双因素方差分析示例

2.1 问题描述

假设A因子有5个水平，B因子有4个水平，两因子间不存在交互作用。观测值无重复，试进行双因素方差分析。

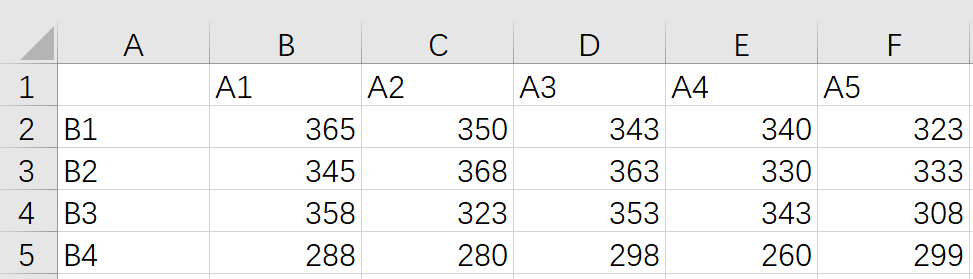
2.2 数据读取并进行预处理

将上述问题中数据整理成数据文件data.csv(参看上图），完了利用R语言整理为tidy-date数据。！！！

dd=read.csv("data.csv",header = T,row.names = NULL)
head(dd)
X  A1  A2  A3  A4  A5
1 B1 365 350 343 340 323
2 B2 345 368 363 330 333
3 B3 358 323 353 343 308
4 B4 288 280 298 260 299

library(tidyr)
names(dd)    #查看列名
colnames(dd)[1] <- 'B'     #修改第一列行名为B
data1<- gather(dd,A,Y,-B)

  B  A   Y
1 B1 A1 365
2 B2 A1 345
3 B3 A1 358
4 B4 A1 288
5 B1 A2 350
6 B2 A2 368

#将字符型变量转化为因子型
data1$A<- factor(data1$A,levels = c("A1","A2","A3","A4","A5"),
                 labels = c(1:5) )
data1$B<- factor(data1$B,levels =c("B1","B2","B3","B4"),
                 labels = c(1:4))

  B A   Y
1 1 1 365
2 2 1 345
3 3 1 358
4 4 1 288
5 1 2 350
6 2 2 368

2.3 对数据进行正态性、方差齐次检验

shapiro.test(data1$Y)      #正态性检验
bartlett.test(data1$Y ~ data1$A, data=data1)   #方差齐次检验
bartlett.test(data1$Y ~ data1$B, data=data1)

#shapiro.test(data1$Y)
	Shapiro-Wilk normality test
data:  data1$Y
W = 0.9358, p-value = 0.1996
#bartlett.test(data1$Y ~ data1$A, data=data1)
	Bartlett test of homogeneity of variances
data:  data1$Y by data1$A
Bartlett's K-squared = 2.44, df = 4, p-value = 0.6554
#bartlett.test(data1$Y ~ data1$B, data=data1)
	Bartlett test of homogeneity of variances
data:  data1$Y by data1$B
Bartlett's K-squared = 0.45668, df = 3, p-value = 0.9283

由P值，数据满足正态性假设，因素A、B均满足方差齐性要求。

2.4 R语言计算

#  进行双因素方差分析
aov_data1<-aov(Y~A+B, data=data1)
#  查看结果
aov_data1
summary(aov_data1)

aov(formula = Y ~ A + B, data = data1)
Terms:
                      A       B Residuals
Sum of Squares   1986.0 12917.4    2925.6
Deg. of Freedom       4       3        12

Residual standard error: 15.6141
Estimated effects may be unbalanced

summary(aov_data1)
            Df Sum Sq Mean Sq F value   Pr(>F)
A            4   1986     497   2.037 0.153021
B            3  12917    4306  17.661 0.000107 ***
Residuals   12   2926     244
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

结果中B这行P值<0.0001，同时自动标注了显著程度，可见B因子之间在0.01%水平上差异显著，A这行P值>0.05，没有任何标注，说明A因子之间差异不显著。*

总结

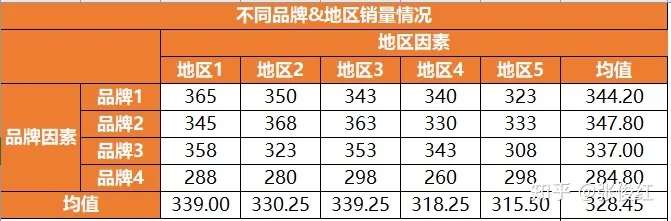
在实际问题的研究中，有时需要考虑两个因素对实验结果的影响。例如饮料销售，除了关心饮料品牌之外，我们还想了解销售地区是否影响销售量，如果在不同的地区，销售量存在显著的差异，就需要分析原因。采用不同的销售策略， 使该饮料品牌在市场占有率高的地区继续深入人心，保持领先地位；在市场占有率低的地区，进一步扩大宣传，让更多的消费者了解、接受该产品。若 把饮料的品牌看作影响销售量的因素A，饮料的销售地区则是影响因素B。对因素A和因素B同时进行分析，就属于双因素方差分析的内容， 双因素方差分析是对影响因素进行检验，究竟是一个因素在起作用，还是两个因素都起作用，或是两个因素的影响都不显著。

参考文献

R语言对完全随机分组实验、拉丁方实验及正交实验进行方差分析

语言数据分析笔记——方差分析