数值分析——插值（一）、Runge现象

在数值分析中，插值方法是基础且重要的。本文将介绍Lagrange插值公式与Newton插值公式。此外，针对Runge现象，本文给出了稍稍详细的讨论。

一、Lagrange插值公式

假设函数 \(y=f(x)\) 在取定的\(n+1\)个互异的基点 \(x_0,x_1,\cdots,x_n\) 处的值已知分别为 \(y_0=f(x_0),y_1=f(x_1),\cdots,y_n=f(x_n)\)，现在要寻找多项式 \(p(x)\) 使得 $$p(x_k)=f(x_k), \quad k=0,1,\cdots,n$$

记

\[l_i(x)=\prod_{j=0, j \neq i}^n \frac{x-x_j}{x_i-x_j},\quad i=0,1,\cdots,n
\]

令

\[p_n(x)=\sum_{i=0}^nf(x_i)l_i(x)
\]

这就是满足条件的多项式。

例 利用等距基点计算函数 \(f(x)=\frac{\sin{e^{-x^2}}}{\sqrt{x+2}}\) 在区间 \([-1,1]\) 上的值。

import math
def fun1(t):
    return math.sin(math.exp(-t**2))/math.sqrt(t+2)

def LagIn(X,P,x):
    Pol=0
    length=len(P)
    count1=0
    while count1 <= length-1:
        lpoly=P[count1]
        count2=0
        while count2 <= length-1:
            if count1 != count2:
                lpoly=lpoly*(x-X[count2])/(X[count1]-X[count2])
            else:
                lpoly=lpoly
            count2=count2+1
        Pol=Pol+lpoly
        count1=count1+1
    return Pol    

n=int(input("输入基点个数："))
A=[]
K=[]
Result=[]
count=0
while count <= n:
    A.append(fun1(-1+count*2/n))
    K.append(-1+count*2/n)
    count=count+1
count=0
print(LagIn(K,A,0.1))

考虑误差问题。记

\[r_n(x)=f(x)-p_n(x)
\]

若\(f(x)\)在包含\(n+1\)个插值基点\(x_0,x_1,\cdots,x_n\)的区间\([a,b]\)上有\(n\)阶连续导数，且在\((a,b)\)内存在\(n+1\)阶有界导数，那么对\([a,b]\)上的每一点\(x\)必存在一点\(\eta \in (a,b)\)使得

\[r_n(x)=\frac{f^{(n+1)}(\eta)}{(n+1)!}\prod_{i=0}^n(x-x_i)
\]

二、均差与Newton插值公式

仍然使用上一节的记号。考虑形如

\[N_n(x)=a_0+a_1(x-x_0)+a_2(x-x_0)(x-x_1)+\cdots+a_n(x-x_0)(x-x_1)\cdots(x-x_{n-1})
\]

的多项式，满足条件

\[N_n(x_i)=f(x_i),\quad i=0,1,\cdots,n
\]

由线性代数的知识容易知道，\(a_0,a_1,\cdots,a_n\)是唯一确定的。考虑这种形式的多项式的好处是，当需要增加基点时，可以减少计算量。

下面引入均差的概念来确定该插值多项式的系数。

\(f(x)\)关于基点\(x_0,x_1,\cdots,x_n\)的n阶均差定义为

\[f[x_0,x_1,\cdots,x_n]=\frac{f[x_1,x_2,\cdots,x_n]-f[x_0,x_1,\cdots,x_{n-1}]}{x_n-x_0}
\]

规定

\[f[x_i]=f(x_i)
\]

是\(f(x)\)关于基点\(x_i\)的零阶均差。

利用数学归纳法可以证明：n阶均差可以写成

\[f[x_0,x_1,\cdots,x_n]=\sum_{i=0}^n\frac{f(x_i)}{\prod_{j=0,j\neq i}^n(x_i-x_j)}
\]

与利用Lagrange插值法得到的多项式比较可知，\(N_n(x)\)的系数

\[a_k=f[x_0,x_1,\cdots,x_k],\quad k=0,1,\cdots,n
\]

三、Runge现象

考虑函数

\[f(x)=\frac{1}{1+x^2},\quad x\in [-5,5]
\]

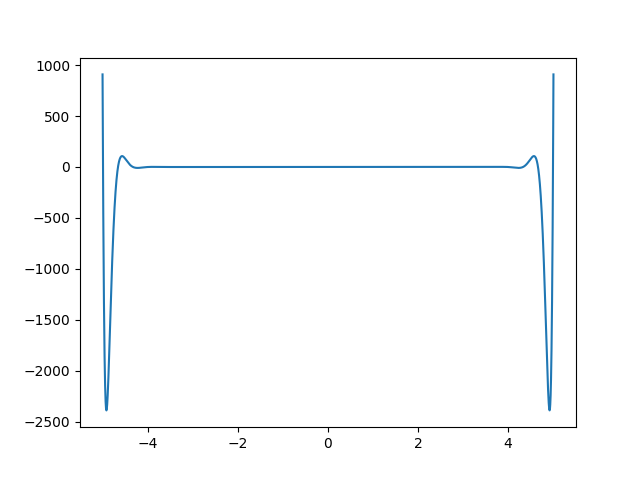
对该函数在等距基点上插值，分别取插值基点个数为5，10，15，20，30，作出误差图像，如下所示：

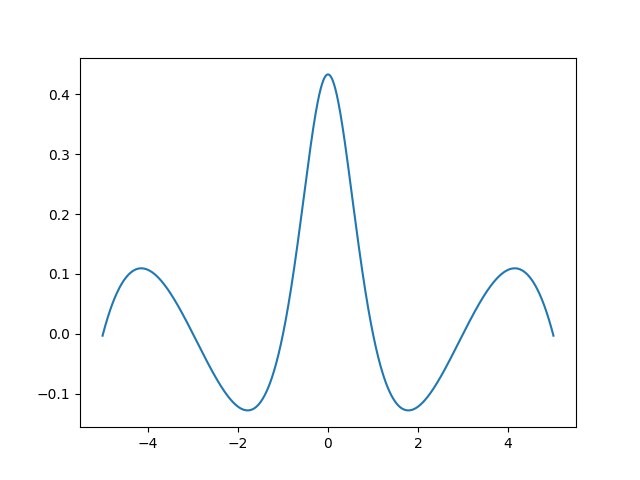
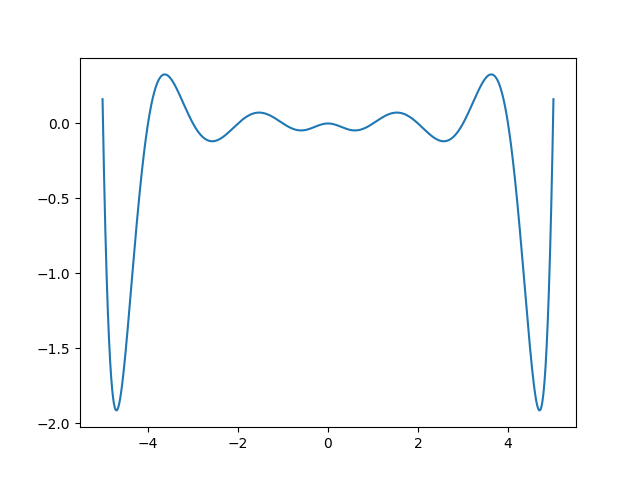
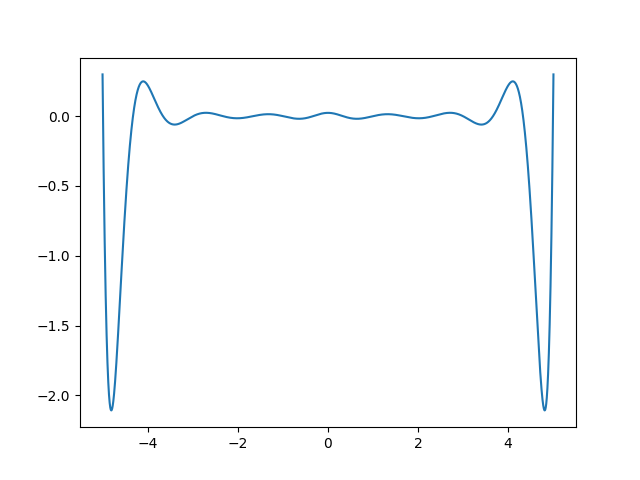
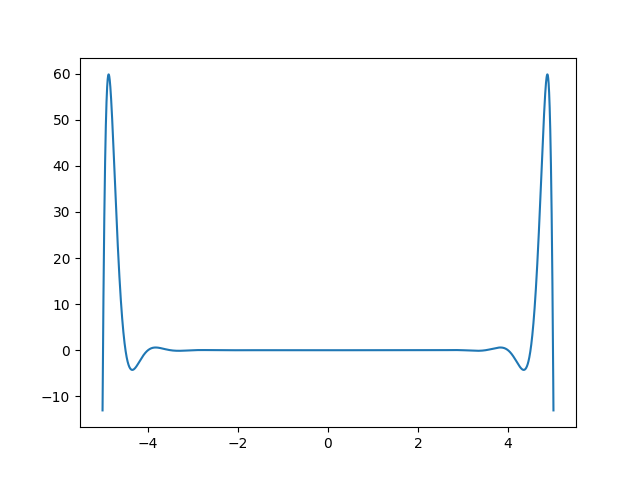
import math
import matplotlib.pyplot as mpl
def fun1(t):
    return (1+t**2)**(-1)

def LagIn(X,P,x):
    Pol=0
    length=len(P)
    count1=0
    while count1 <= length-1:
        lpoly=P[count1]
        count2=0
        while count2 <= length-1:
            if count1 != count2:
                lpoly=lpoly*(x-X[count2])/(X[count1]-X[count2])
            else:
                lpoly=lpoly
            count2=count2+1
        Pol=Pol+lpoly
        count1=count1+1
    return Pol    

n=int(input("输入基点个数："))
A=[]
K=[]
Result=[]
count=0
while count <= n:
    A.append(fun1(-5+count*10/n))
    K.append(-5+count*10/n)
    count=count+1
count=0
B=[]
F=[]
while count <= 10000:
    B.append(-5.01+count*10.02/10000)
    F.append((fun1(B[count])-LagIn(K,A,B[count])))
    count=count+1

mpl.plot(B,F)
mpl.show()

可以看到，插值多项式在端点附近有较大的误差。事实上可以证明

\[\lim_{n \to \infty}\max_{x \in [-5,5]}|f(x)-p_n(x)|= \infty
\]

这就是所谓的Runge现象。下面将进行仔细讨论。

在区间\([a,b]\)上，记插值基点为\(\{x_j^{(n)}\},\quad j=0,1,\cdots,n\)，插值多项式为\(p_n(x)\)。首先估计误差项\(f(x)-p_n(x)\)。

由Newton插值法，在区间\([a,b]\)上取与插值基点相异的一个基点 \(x=t\)，得到

\[p_{n+1}(x)=p_n(x)+f[x_0,x_1,\cdots,x_n,t](x-x_0)(x-x_1)\cdots(x-x_n)
\]

由于\(p_{n+1}(t)=f(t)\)，因此

\[f(x)-p_n(x)=f[x_0,x_1,\cdots,x_n,x]\prod_{j=0}^n(x-x_{j}^{(n)})
\]

下面记

\[\omega_n(x)=\prod_{j=0}^n(x-x_{j}^{(n)})
\]

下面在复平面上考虑问题，插值基点视作实轴上的点，仍保留原来的记号。

由留数定理

\[f[x_0,x_1,\cdots,x_n]=\sum_{i=0}^n\frac{f(x_i)}{\prod_{j=0,j\neq i}^n(x_i-x_j)}=\sum_{i=0}^n\mathrm{Res}(\mathrm{g},x_i)=\frac{1}{2\pi i}\int_Cg(z)\mathrm{d}z
\]

其中

\[g(z)=\frac{f(z)}{\prod_{i=0}^n(z-x_i)}
\]

C是曲线，使得插值基点在它内部，\(f\)在其内部解析。类似可以求得\(f[z,x_0,x_1,\cdots,x_n]\)的表达式。从而得到

\[f(z)-p_n(z)=\frac{1}{2\pi i}\int_C\frac{\omega_n(z)}{\omega_n(\eta)}\frac{f(\eta)}{\eta-z}\mathrm{d}\eta
\]

为了进一步估计，需要先证明以下引理：

引理 假设\(\{x_j^{(n)}\}\)是区间\([a,b]\)上的等距基点，定义

\[\sigma_n(z)=|\omega_n(z)|^{\frac{1}{n+1}}
\]

则

\[\lim_{n\to \infty}\sigma_n(z)=\sigma(z)=\mathrm{exp}\{\frac{1}{b-a}\int_a^b \mathrm{ln}|z-s|\mathrm{d}s\}
\]

证明：

\[\mathrm{ln}\sigma_n(z)=\frac{1}{n+1}\sum_{i=0}^n \mathrm{ln}|z-a-\frac{b-a}{n}i|
\]

由黎曼积分的定义知

\[\lim_{n\to \infty}\mathrm{ln}\sigma_n(z)=\frac{1}{b-a}\int_a^b\mathrm{ln}|z-s|\mathrm{d}s
\]

引理成立。

考虑曲线

\[C(\rho)=\{z \in \mathbb{C}|\sigma(z)=\rho \}
\]

命题 \(\{x_j^{(n)}\}\)是包含在曲线\(C(\rho)\)中的等距插值基点，若\(f\)在\(C(\rho)\)中解析，则\(p_n\)在\(C(\rho'),\rho' < \rho\)上一致收敛于\(f\)。

证明：假设\(z\)在曲线\(C(\rho')\)上，显然\(C(\rho)\)和\(C(\rho')\)是不交的，因此有以下估计：

\[|f(z)-p_n(z)|\leq\frac{1}{2\pi i}\int_{C(\rho)}|\frac{\omega_n(z)}{\omega_n{(\eta)}}||\frac{f(\eta)}{\eta-z}|\mathrm{d}\eta
\]

由于\(|f(\eta)|\)和\(|\eta-z|\)在\(C(\rho)\)上分别由上界和下界，因此

\[|f(z)-p_n(z)|\leq A \max_{\eta \in C(\rho)}|\frac{\omega_n(z)}{\omega_n(\eta)}|
\]

考虑引理中的结果，由\(\lim_{n \to \infty}\sigma_n(z)=\rho'\)及\(\lim_{n \to \infty}\sigma_n(\eta)=\rho\)，对\(\epsilon < \frac{|p-p'|}{3}\)能够取到\(n\)使得

\[|\frac{\omega_n(z)}{\omega_n(\eta)}|^\frac{1}{n+1}=\frac{\sigma_n(z)}{\sigma_n(\eta)}\leq \frac{\rho'+\epsilon}{\rho-\epsilon}<1
\]

从而可以证明一致收敛。

考虑\(f\)在\(C(\rho)\)中并不解析的情况。仅仅讨论一种特殊情况：若只有一个一阶极点\(z^*\)，此时

\[f(z)-p_n(z)=\frac{1}{2\pi i}\int_{C(\rho)}\frac{\omega_n(z)}{\omega_n(\eta)}\frac{f(\eta)}{\eta-z}\mathrm{d}\eta+\frac{1}{2\pi i}\int_{C^*}\frac{\omega_n(z)}{\omega_n(\eta)}\frac{f(\eta)}{\eta-z}\mathrm{d}\eta
\]

其中\(C^*=C(\rho^*)\)是围绕极点的一条路径。由上面的讨论知，第一项趋于零。利用留数定理，第二项可以写成

\[B\frac{\omega_n(z)}{\omega_n(z^*)}
\]

其中

\[B=\lim_{\eta \to z^*}\frac{f(\eta)}{(\eta-z^*)(\eta-z)}
\]

是有界的。

\[|\frac{\omega_n(z)}{\omega_n(z^*)}|^\frac{1}{n+1}=\frac{\sigma_n(z)}{\sigma_n(z^*)}\geq\frac{\rho'-\epsilon}{\rho^*+\epsilon}>1
\]

此时\(f(z)-p_n(z)\)并不收敛。

上面的讨论并没有给出Runge现象的充要条件。当插值区间过大时，可能会出现Runge现象；缩小插值区间，可以避免Runge现象，因此可以考虑分段插值的方法。此外也可以采用Chebyshev基点进行插值，这就不在本文的讨论范围内了。

---

参考

[1]Epperson J. On the Runge Example[J]. The American Mathematical Monthly, 1987, 94(4):329-341.

[2]林成森. 数值计算方法[M]. 科学出版社, 2005.

[3]作者本人的实验报告.