Expm 4_1 多段图中的最短路径问题

 

【问题描述】

建立一个从源点S到终点T的多段图，设计一个动态规划算法求出从S到T的最短路径值，并输出相应的最短路径。

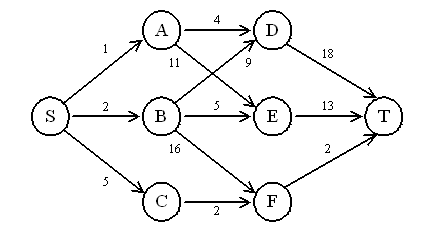
解

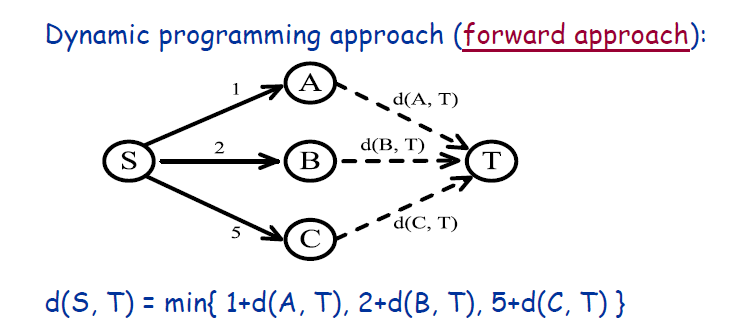
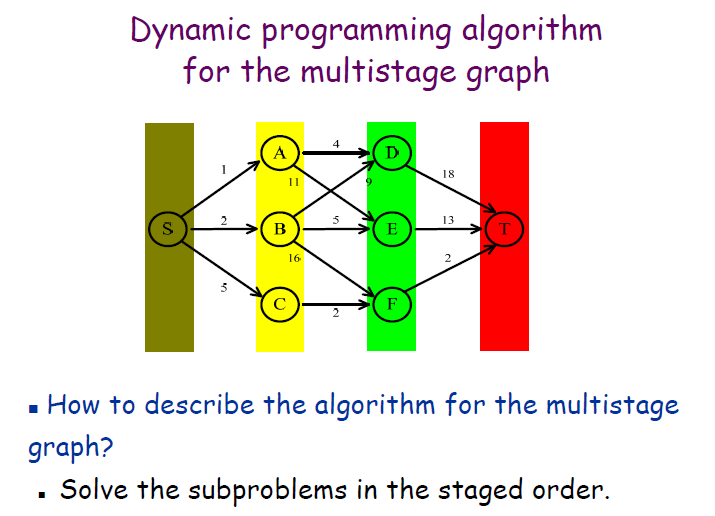
 package org.xiu68.exp.exp4;

 public class Exp4_1 {
     //建立一个从源点S到终点T的多段图，设计一个动态规划算法求出从S到T的最短路径值，并输出相应的最短路径。
     /*
     d[1] = 0
     for j = 2 to n:
     for all <i,j>∈E :
     d[j] = min{ d[i] + wij }
     return d[n]
     */
     public static void main(String[] args) {
         // TODO Auto-generated method stub
         int m=Integer.MAX_VALUE;
         int[][] edges=new int[][]{
             {m,1,2,5,m,m,m,m},
             {m,m,m,m,4,11,m,m},
             {m,m,m,m,9,5,16,m},

             {m,m,m,m,m,m,2,m},
             {m,m,m,m,m,m,m,18},
             {m,m,m,m,m,m,m,13},

             {m,m,m,m,m,m,m,2},
             {m,m,m,m,m,m,m,m},
         };

         MGraph graph1=new MGraph(edges);
         graph1.minMultistageGraphPath(0, 7);

     }

 }

 class MGraph{
     private int[][] edges;        //有向图表示多段图
     private int vexNum;            //顶点数量

     public MGraph(int[][] edges){
         this.edges=edges;
         this.vexNum=edges.length;
     }

     public void minMultistageGraphPath(int start,int end){
         int[] dist=new int[vexNum];        //从源点到该点的路径长度
         dist[start]=0;

         int[] pre=new int[vexNum];        //在最短路径中该点的前一个顶点
         pre[start]=-1;

         for(int j=1;j<vexNum;j++){    

             dist[j]=Integer.MAX_VALUE;
             pre[j]=-1;

             for(int i=0;i<vexNum;i++){
                 if(edges[i][j]!=Integer.MAX_VALUE && dist[j]>dist[i]+edges[i][j]){
                     dist[j]=dist[i]+edges[i][j];
                     pre[j]=i;
                 }
             }
         }

         //打印最短路径
         System.out.println(start+" to "+end+" is "+dist[end]);

         String path=""+end;
         int preVex=pre[end];

         while(preVex!=-1){
             path=preVex+"-->"+path;
             preVex=pre[preVex];
         }
         System.out.println("the path is:"+path);
     }
 }