【做题】TCSRM591 Div1 500 PyramidSequences——数形结合&思维

题意：定义高度为\(x\)的金字塔数列为周期为\(2x-2\)的无限数列。它的每一个周期都是形如\(1,2,...,x-1,x,x-1,...,2\)的形式。记高度为\(x\)的金字塔数列第\(i\)个数为\(p_{x,i}\)

现在给出\(n\)和\(m\)，求集合\(S = \{(x,y) | \, \exists i , x = A_{n,i}, y = A_{m,i}\}\)的大小。

\(n,m \leq 10^9\)

遇到此题似乎无从下手。在于我们无从直接处理数列。

考虑把\((x,y)\)的二元组放在二维坐标系上。那么，一个金字塔数列就是在来回反弹，而两个就是在二维网格图上来回反弹，直至到达四个终点中的任意一个。这个网格图的边长为\(n-1\)和\(m-1\)。于是形成了与坐标轴夹角为\(45^{\circ}\)的折线。

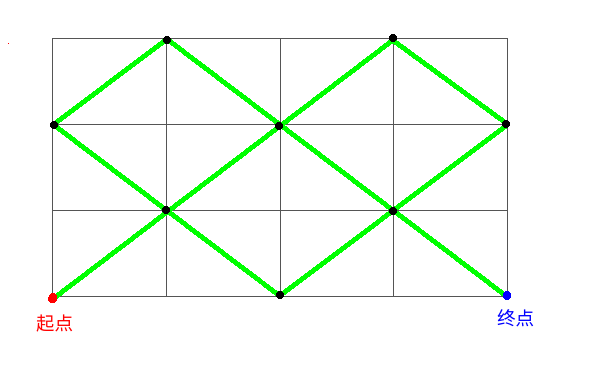
现在，我们要求的就是所到达的格点数量。设图边长分别为\(a\)和\(b\)。

问题在于一个结点到达多次只算一次。否则就通过镜面展开的套路，得到答案为\(\frac {ab} {gcd(a,b)}\)。这也就是我们所能走的路径长度。

考虑\(a,b\)互质的情况。那么，我们走的路径长度为\(ab\)。注意到图上也正好有\(ab\)个网格。因为我们只沿对角线走，所以所有经过结点的横坐标和纵坐标的和的奇偶性是一定的。考虑一个方格，它边上的4个格点中只有两个是有可能经过的，而要穿过这个方格，就只能走那两个格点的连线。显然，路径上的边是不重的。因此，每个方格最多被经过1次，则路径长度小于等于\(ab\)。而它事实上正等于\(ab\)，这说明每个网格都被穿过了，那么，所有可能经过的格点都经过了。于是，经过的格点数就是\(\left\lceil \frac {(a+1)(b+1)} {2} \right\rceil\)。

而当\(a,b\)不互质时，设\(gcd(a,b)=d, \, a = a' d , \, b = b' d\)，那就相当于把原来的网格放大\(d\)倍。每个小网格都变成了一个\(d \times d\) 的大网格。因此，穿过一个大网格时，还会再经过\(d-1\)个格点，它们只会经过1次。所以答案再加上\(a'b' \times (d-1)\)就可以了。

时间复杂度\(O(\log n)\)。

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
class PyramidSequences {
public:
    long long distinctPairs( int N, int M );
};
long long PyramidSequences::distinctPairs(int N, int M) {
  N --;
  M --;
  ll d = __gcd(N,M);
  ll x = N / d, y = M / d;
  ll ret = ((x + 1) * (y + 1) + 1) / 2;
  ret += x * y * (d-1);
  return ret;
}

小结：TC的题目还是很有灵活性的。在数形结合基础上，拓展经典问题，这还是有难度的。