浅谈压缩感知（二十四）：压缩感知重构算法之子空间追踪（SP）

主要内容：

1. SP的算法流程
2. SP的MATLAB实现
3. 一维信号的实验与结果
4. 测量数M与重构成功概率关系的实验与结果
5. SP与CoSaMP的性能比较

一、SP的算法流程

压缩采样匹配追踪(CoSaMP)与子空间追踪（SP）几乎完全一样，因此算法流程也基本一致。

SP与CoSaMP主要区别在于"Ineach iteration, in the SP algorithm, only K new candidates are added, while theCoSAMP algorithm adds 2K vectors."，即SP每次选择K个原子，而CoSaMP则选择2K个原子；这样带来的好处是"This makes the SP algorithm computationally moreefficient,"。

SP的算法流程：

这个算法流程的初始化(Initialization)其实就是类似于CoSaMP的第1次迭代，注意第(1)步中选择了K个原子："K indices corresponding to the largest magnitude entries"，在CoSaMP里这里要选择2K个最大的原子，后面的其它流程都一样。这里第(5)步增加了一个停止迭代的条件：当残差经过迭代后却变大了的时候就停止迭代。

具体的算法步骤与浅谈压缩感知（二十三）：压缩感知重构算法之压缩采样匹配追踪（CoSaMP）一致，只需将第(2)步中的2K改为K即可。

"贪婪类算法虽然复杂度低运行速度快，但其重构精度却不如BP类算法，为了寻求复杂度和精度更好地折中，SP算法应运而生"，"SP算法与CoSaMP算法一样其基本思想也是借用回溯的思想，在每步迭代过程中重新估计所有候选者的可信赖性"，"SP算法与CoSaMP算法有着类似的性质与优缺点"。

二、SP的MATLAB实现(CS_SP.m)

function [ theta ] = CS_SP( y,A,K )
%   CS_SP
%   Detailed explanation goes here
%   y = Phi * x
%   x = Psi * theta
%    y = Phi*Psi * theta
%   令 A = Phi*Psi, 则y=A*theta
%   K is the sparsity level
%   现在已知y和A，求theta
%   Reference:Dai W，Milenkovic O．Subspace pursuit for compressive sensing
%   signal reconstruction[J]．IEEE Transactions on Information Theory，
%   ，()：-.
    [m,n] = size(y);
    if m<n
        y = y'; %y should be a column vector
    end
    [M,N] = size(A); %传感矩阵A为M*N矩阵
    theta = zeros(N,); %用来存储恢复的theta(列向量)
    pos_num = []; %用来迭代过程中存储A被选择的列序号
    res = y; %初始化残差(residual)为y
    for kk=:K %最多迭代K次
        %() Identification
        product = A'*res; %传感矩阵A各列与残差的内积
        [val,pos]=sort(abs(product),'descend');
        Js = pos(:K); %选出内积值最大的K列
        %() Support Merger
        Is = union(pos_num,Js); %Pos_theta与Js并集
        %() Estimation
        %At的行数要大于列数，此为最小二乘的基础(列线性无关)
        if length(Is)<=M
            At = A(:,Is); %将A的这几列组成矩阵At
        else %At的列数大于行数，列必为线性相关的,At'*At将不可逆
            break; %跳出for循环
        end
        %y=At*theta，以下求theta的最小二乘解(Least Square)
        theta_ls = (At'*At)^(-1)*At'*y; %最小二乘解
        %() Pruning
        [val,pos]=sort(abs(theta_ls),'descend');
        %() Sample Update
        pos_num = Is(pos(:K));
        theta_ls = theta_ls(pos(:K));
        %At(:,pos(:K))*theta_ls是y在At(:,pos(:K))列空间上的正交投影
        res = y - At(:,pos(:K))*theta_ls; %更新残差
        if norm(res)<1e- %Repeat the steps until r=
            break; %跳出for循环
        end
    end
    theta(pos_num)=theta_ls; %恢复出的theta
end

三、一维信号的实验与结果

%压缩感知重构算法测试
clear all;close all;clc;
M = ; %观测值个数
N = ; %信号x的长度
K = ; %信号x的稀疏度
Index_K = randperm(N);
x = zeros(N,);
x(Index_K(:K)) = *randn(K,); %x为K稀疏的，且位置是随机的
Psi = eye(N); %x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
Phi = randn(M,N); %测量矩阵为高斯矩阵
A = Phi * Psi; %传感矩阵
y = Phi * x; %得到观测向量y

%% 恢复重构信号x
tic
theta = CS_SP( y,A,K );
x_r = Psi * theta; % x=Psi * theta
toc

%% 绘图
figure;
plot(x_r,'k.-'); %绘出x的恢复信号
hold on;
plot(x,'r'); %绘出原信号x
hold off;
legend('Recovery','Original')
fprintf('\n恢复残差：');
norm(x_r-x) %恢复残差

四、测量数M与重构成功概率关系的实验与结果

clear all;close all;clc;

%% 参数配置初始化
CNT = ; %对于每组(K,M,N)，重复迭代次数
N = ; %信号x的长度
Psi = eye(N); %x本身是稀疏的，定义稀疏矩阵为单位阵x=Psi*theta
K_set = [,,,,]; %信号x的稀疏度集合
Percentage = zeros(length(K_set),N); %存储恢复成功概率

%% 主循环，遍历每组(K,M,N)
tic
for kk = :length(K_set)
    K = K_set(kk); %本次稀疏度
    M_set = *K::N; %M没必要全部遍历，每隔5测试一个就可以了
    PercentageK = zeros(,length(M_set)); %存储此稀疏度K下不同M的恢复成功概率
    for mm = :length(M_set)
       M = M_set(mm); %本次观测值个数
       fprintf('K=%d,M=%d\n',K,M);
       P = ;
       for cnt = :CNT %每个观测值个数均运行CNT次
            Index_K = randperm(N);
            x = zeros(N,);
            x(Index_K(:K)) = *randn(K,); %x为K稀疏的，且位置是随机的
            Phi = randn(M,N)/sqrt(M); %测量矩阵为高斯矩阵
            A = Phi * Psi; %传感矩阵
            y = Phi * x; %得到观测向量y
            theta = CS_SP(y,A,K); %恢复重构信号theta
            x_r = Psi * theta; % x=Psi * theta
            if norm(x_r-x)<1e- %如果残差小于1e-6则认为恢复成功
                P = P + ;
            end
       end
       PercentageK(mm) = P/CNT*; %计算恢复概率
    end
    Percentage(kk,:length(M_set)) = PercentageK;
end
toc
save SPMtoPercentage1000 %运行一次不容易，把变量全部存储下来

%% 绘图
S = ['-ks';'-ko';'-kd';'-kv';'-k*'];
figure;
for kk = :length(K_set)
    K = K_set(kk);
    M_set = *K::N;
    L_Mset = length(M_set);
    plot(M_set,Percentage(kk,:L_Mset),S(kk,:));%绘出x的恢复信号
    hold on;
end
hold off;
xlim([ ]);
legend('K=4','K=12','K=20','K=28','K=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');

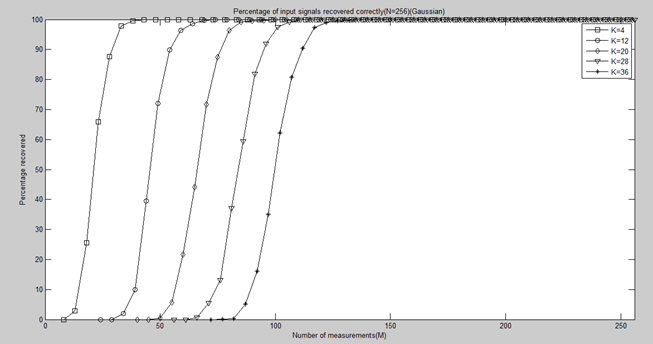
五、SP与CoSaMP的性能比较

分别运行SP和CoSaMP中的"测量数M与重构成功概率关系的实验与结果"后，将相关变量load进来，并画在同一张图上，即可看出孰优孰劣。

clear all;close all;clc;
load CoSaMPMtoPercentage1000;
PercentageCoSaMP = Percentage;
load SPMtoPercentage1000;
PercentageSP = Percentage;
S1 = ['-ks';'-ko';'-kd';'-kv';'-k*'];
S2 = ['-rs';'-ro';'-rd';'-rv';'-r*'];
figure;
for kk = :length(K_set)
    K = K_set(kk);
    M_set = *K::N;
    L_Mset = length(M_set);
    plot(M_set,PercentageCoSaMP(kk,:L_Mset),S1(kk,:));%绘出x的恢复信号
    hold on;
    plot(M_set,PercentageSP(kk,:L_Mset),S2(kk,:));%绘出x的恢复信号
end
hold off;
xlim([ ]);
legend('CoSaK=4','SPK=4','CoSaK=12','SPK=12','CoSaK=20',...
    'SPK=20','CoSaK=28','SPK=28','CoSaK=36','SPK=36');
xlabel('Number of measurements(M)');
ylabel('Percentage recovered');
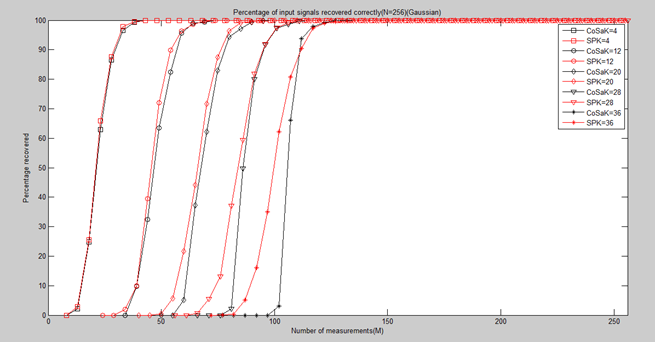
title('Percentage of input signals recovered correctly(N=256)(Gaussian)');

结论：从总体上看，SP优于CoSaMP（尤其是在M较小的时候）

六、参考文章

http://blog.csdn.net/jbb0523/article/details/45441459