混沌的艺术--- YChaos通过数学公式生成混沌图像

艺术真得很难吗?也许如同编程一样容易。我写了一套软件，其功能是通过输入数学方程式，生成艺术图像。一提到数学有人可能会发怵，这里请不要担心，生成混沌的数学公式大都很是简单，基本上只用加、减、乘、除、余、正弦、余弦这七种运算。说到数学，在我心里也留有一大片阴影，别问我阴影面积有多大，因为我算不出来。依然记得当年的数学考试，每次其最后一道BOSS题，我是从来没有做出来过。再说高等数学的微积分，十年前我学得还算可以，但应付完考试就被废了。而现在文档论文上的公式大多都要整几个微积分来提高逼格，我一看到就怵。几年前参加一个面试，问我如何求椭球面上任意两点的距离，我就说你在椭球上给这两点穿个洞，两点的距离就是其直线距离。前些日子我读小说三体，于是也研究了下三体，并写了两个关于三体和N体的小程序。只是我写的程序其精确性是不够的，因为没有使用微积分。本来打算重学下高数，并专门从故纸堆里翻出了当年大学时的高数课本，结果到现在也没翻过几页。

好吧有些跑题了，再拉回来谈混沌。什么是混沌？数学上的混沌和庄子所说的混沌，虽有相似之处但不是一个东西。我的理解是：混沌就是不确定性。你可能知道混沌公式生成值的一个范围，但难以得知其具体为何值。如何实现这种不确定，有两种办法，一个是随机，另一个是迭代。

先讲随机，我曾思考过一个问题：世上有真正的随机吗？我的结论是：莫须有。我对随机的理解是：无法明确计算，它是确定的反义。先说计算机中的随机数rand(),大家都知道这实际上是伪随机数。只有随机数种子不变，其生成的随机数就是固定的。有个关于随机的实验叫沙丘实验，它是从密封空间中的一点向下滴沙粒，其结论是无法得知哪一个沙粒落下后会造成沙丘的崩塌。并有人说沙粒间的碰撞计算量是随沙粒数目呈指数增长的。但计算量大并不代表能造成随机，也许哪天技术一进度，这就能计算出了呢。再说，用数学的推演法看，两个沙粒的碰撞计算是确定的，那么3个沙粒的碰撞计算也是确定的，从而N个沙粒的碰撞计算亦是确定的。比沙粒更微观的实验是布朗运动，它是粒子在液体中随机的运动，但这粒子的运动依然是与其受力有关，所以理论上也是可计算的。再微观到雪花的生成，空气中的一堆水分子，如何组成雪花。雪花本身就是一个随机的东西，据说两片雪花完全相同的概率是一个天文数字分之一，我不知道如果两片雪花生成时所有的参数都一致，其形态是否完全相同。最后微观到原子及量子物理，原子核中电子在质子周围出现，没有明确的轨迹，似乎是随机。可目前不知道其轨迹规律，不代表它没有。倒是数学上每一个无理数其后面出现的数字应该是随机的。

再讲迭代。迭代的意思是自己的输出再做为自己的输入。记得第一次知道迭代是在大学时上的一门课，课名似乎叫工业控制。我连课名都记不清了，可见对这课讲的什么知识已经全忘了。但是对迭代却很有印象，自己的输出再做为自己的输入，这在当时的我看来这有违伦礼，有背道德啊。这不如同自己产的米田共自己再吃了吗，毁三观啊，有木有！另一个让我觉得毁三观的是：递归，自己调用自己Abnormal。后来，经历了岁月的洗礼后，对迭代和递归也就习以为常了，在这个YChaos软件中，混沌的生成就是用的迭代，而数学表达式的解析算法用得则是递归。通常我们用的数学公式是线性的，而有了迭代则出现了非线性数学。如函数x=sin(t+1.0)这是线性的函数,只要给定t值，x值就可以明确得到。而函数x=sin(x+1.0)则是非线性的，因为将这个函数迭代执行若干次后，如果不一步一步地计算，鬼才知道是什么结果。

最后说下艺术，我认为只要觉得好看就是艺术。这算是比较轻松的，我搞混沌算法就是为了生成些漂亮的图像。我不关心洛伦茨的蝴蝶线圈怎么就和天气有了关系，也不想了解为什么逻辑斯蒂映射图和生育繁殖有毛关系，我只生成艺术图像。

混沌图像：

01洛伦茨吸引子

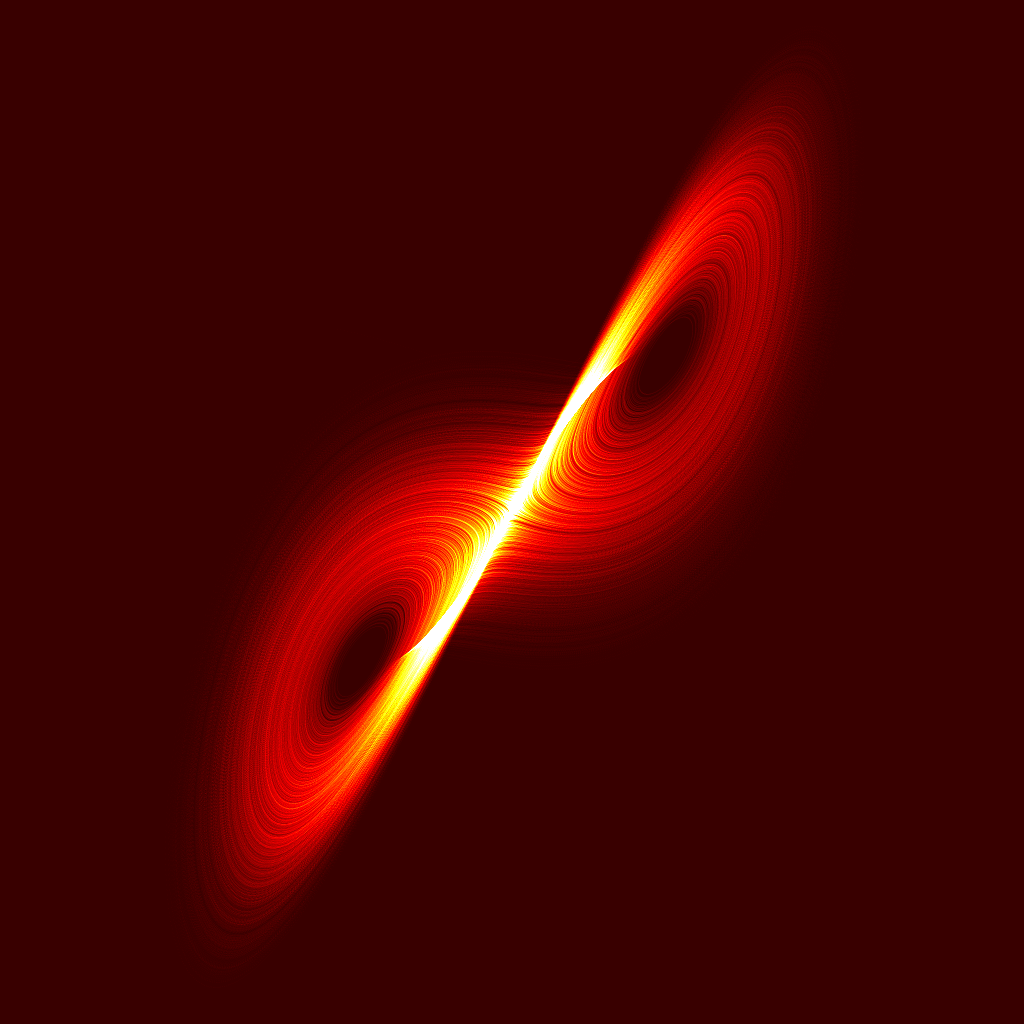
02陈氏吸引子

03吕陈吸引子

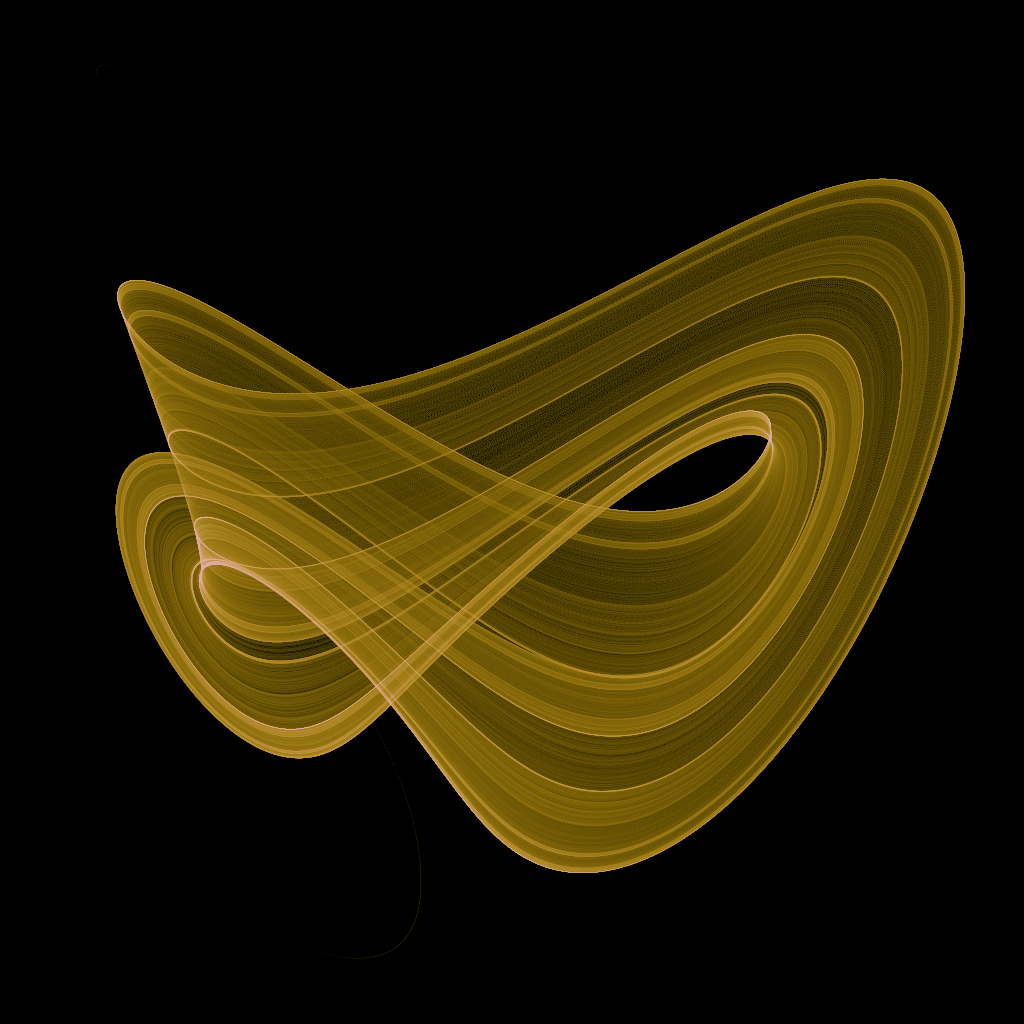
04蔡氏电路

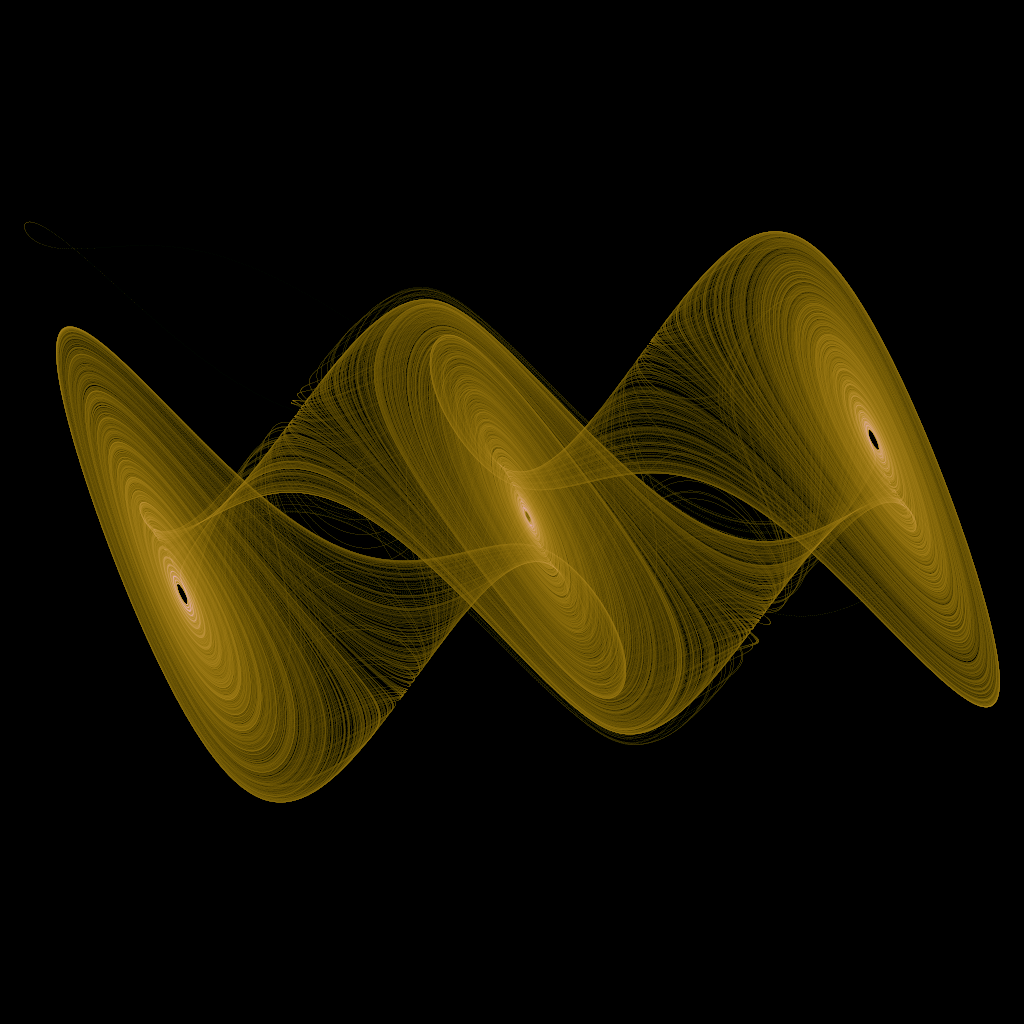
05拉比诺维奇-法布里康特方程

06非线性电路电容中的混沌控制系统

07杜芬方程

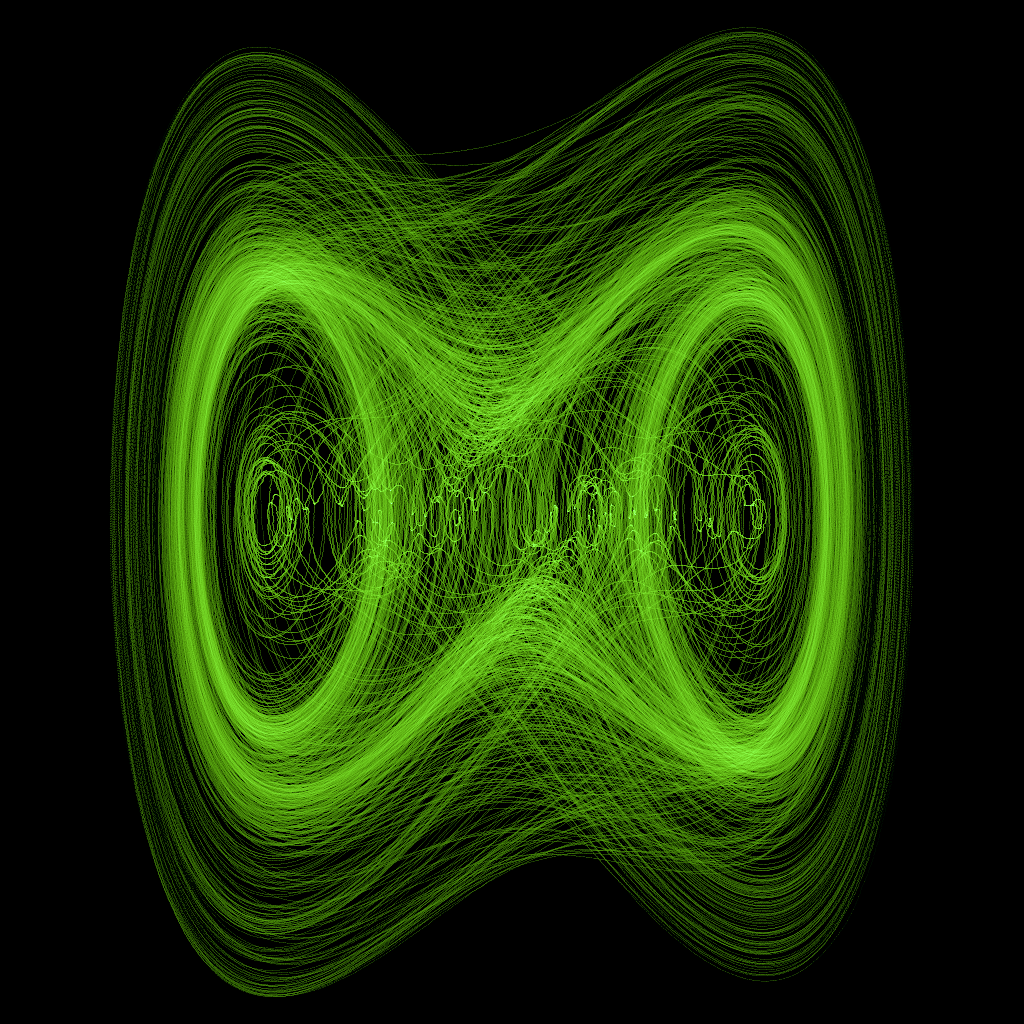
08若斯叻吸引子

09二维离散电路混沌系统

10三体

11玫瑰线

12圆内旋轮线

13圆外旋轮线

14三翅鹰

15国王映射

16马丁迭代

17SinAddCos

18SinMulCos

19SinSubCos

20随机

21谢尔宾斯基

22逻辑斯蒂映射

23曼德勃罗映射

24正弦映射

25标准映射

26标准方程

27埃农映射

28德容吸引子

29Julia

30五星

这里先提供个YChaos软件下载地址和基本使用操作。详细的使用手册容我以后再写。

软件下载地址：http://files.cnblogs.com/files/WhyEngine/YChaos.zip

双击"YChaos图像生成软件.exe"启动软件.

软件有两种模式:编辑模式与图像生成模式。默认打开时为编辑模式，键盘F1用于两种模式的切换。键盘F2用于切换到图像生成模式,并进行图像生成处理。鼠标右键拖动用于设置视口位置，滚轮用于视口的缩放。按下键盘F，会自动设置成最佳视口。按下键盘X则设置成默认大小的视口，这可使图像处于其原始大小显示。

文件夹"images"中存放各种生成图像的配置文件。鼠标将某一配置文件拖入到软件中，即可打开文件。也可以通过菜单项中的文件->打开配置文件...来进行文件选择打开。亦可以使用快捷键CTRL+F来加载配置文件。

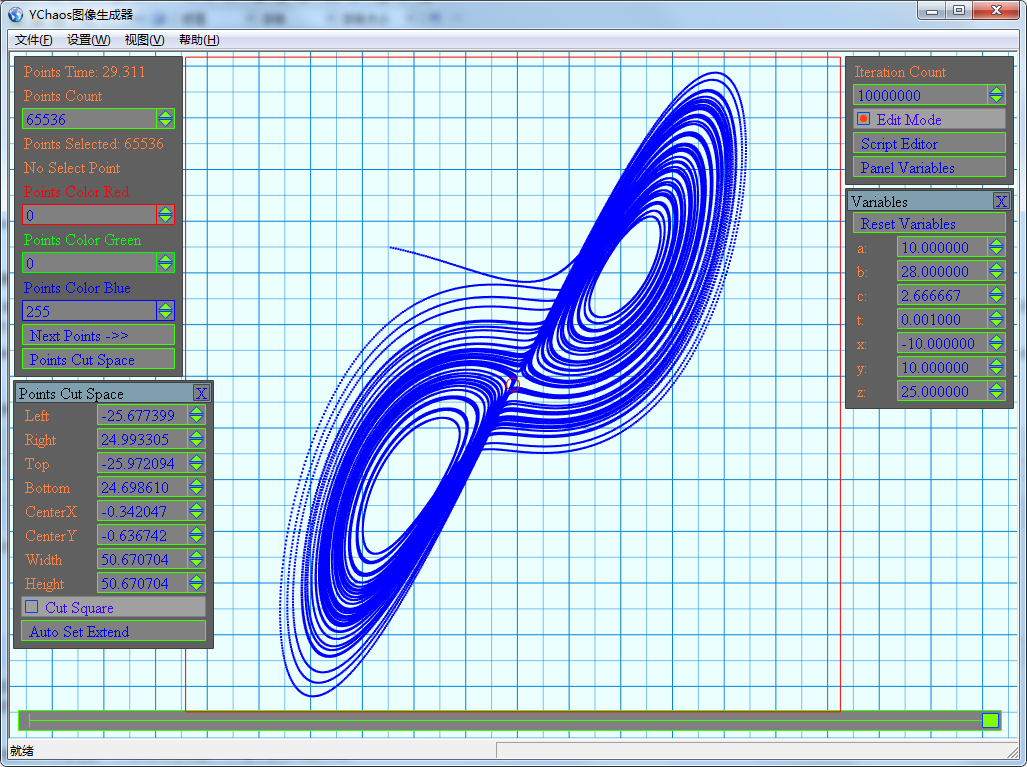
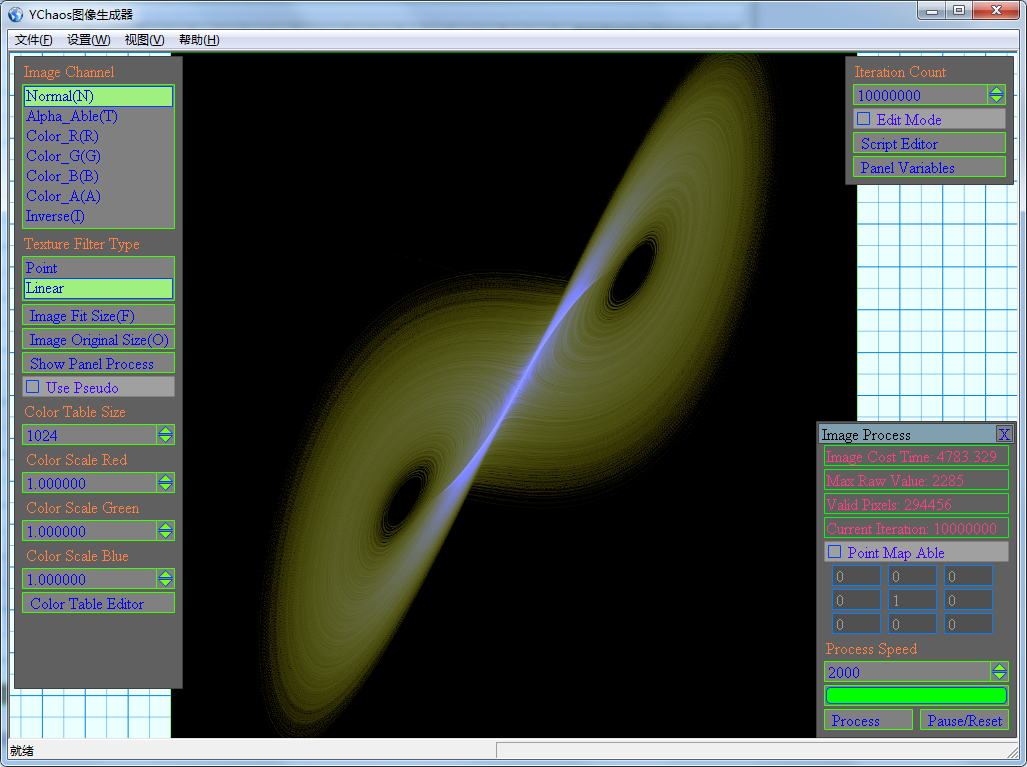
打开某个配置文件后,会切换入编辑模式。按下F2会切换到图像生成模式并生成混沌图像。