POJ 2442 - Sequence - [小顶堆][优先队列]

题目链接：http://poj.org/problem?id=2442

Time Limit: 6000MS Memory Limit: 65536K

Description

Given m sequences, each contains n non-negative integer. Now we may select one number from each sequence to form a sequence with m integers. It's clear that we may get n ^ m this kind of sequences. Then we can calculate the sum of numbers in each sequence, and get n ^ m values. What we need is the smallest n sums. Could you help us?

Input

The first line is an integer T, which shows the number of test cases, and then T test cases follow. The first line of each case contains two integers m, n (0 < m <= 100, 0 < n <= 2000). The following m lines indicate the m sequence respectively. No integer in the sequence is greater than 10000.

Output

For each test case, print a line with the smallest n sums in increasing order, which is separated by a space.

Sample Input

1
2 3
1 2 3
2 2 3

Sample Output

3 3 4

题意：

给出 $m$ 个长度为 $n$ 的序列，在每一个序列中挑选一个数求和，可知有 $n^m$ 个结果，要求给出这些结果中前 $n$ 小的。

题解（参考《算法竞赛进阶指南》）：

首先考虑当 $M=2$ 时的做法，记这两个序列为 $a,b$，先对所有的序列进行升序排序，并且用两个指针 $p,q$ 分别指向这两个序列的头部 $a[0],b[0]$，显然此时就是第 $1$ 小的和 $S_1 = a[0] + b[0]$。

那么，第 $2$ 小的和 $S_2 = \min (a[1] + b[0], a[0] + b[1])$，

如果第 $2$ 小和是 $S_2 = a[1] + b[0]$，那么此时竞争的第 $3$ 小的候选者，除了上面已经存在的 $a[0] + b[1]$ 外还应当再增加 $a[2] + b[0], a[1] + b[1]$，也就是序列一的指针 $ptr_1++$ 或者序列二的指针 $ptr_2++$。

不难想到，可以用一个小顶堆（或者STL的优先队列）来维护所有候选者，不断地扔进去新晋的候选者，再取出堆顶作为答案之一，再由该堆顶求出新的候选者插入堆中，再取出堆顶，反复如此……

候选方案产生方式如图：

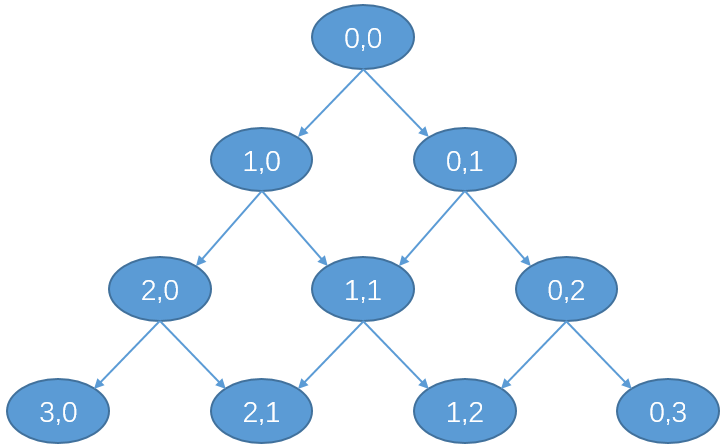
不过，有一点需要注意，例如我们在上述例子中已得 $S_2 = a[1] + b[0]$，那么入堆两个新的候选者之后堆中有三个节点： $a[0] + b[1], a[2] + b[0], a[1] + b[1]$；此时如果 $S_3 = a[0] + b[1]$，会发现又一次产生了候选者 $a[1] + b[1]$，这样就产生了重复，具体表现就是在上图中，就是绝大部分候选方案从 $(0,0)$ 出发可以有多条路径到达。重复方案多次入堆显然是影响正确性的，因此要避免这种情况发生。

不妨增加限定，如果当前选中的方案所产生新的候选者是 $ptr_2++$，那么以后都只能 $ptr_2++$，不能再回到 $ptr_1++$。换句话说，$a[0]+b[0]$ 要走到任何候选方案 $a[i]+a[j]$，必须先移动 $ptr_1 = 0 \sim i$，再移动 $ptr_2 = 0 \sim j$，使得到达备选方案 $a[i]+a[j]$ 的路径的唯一性，这样即可避免产生同一个候选方案重复入队的情况。

增加限定条件后的候选方案产生方式如图（不难看出，已经变为了一棵树）：

考虑到添加了该限定条件后，是否影响到算法的正确性：

考虑原算法在选定 $a[i] + b[j]$ 成为第 $k$ 小之后，原本会产生 $a[i+1] + b[j]$ 和 $a[i] + b[j+1]$ 两个新的候选者。那么增加限定条件后，是否会发生本来第 $k+1$ 小应当是 $a[i+1] + b[j]$ 但是现在却没有生成该候选方案的情况？

根据限定条件，可知 $a[i] + b[j]$ 该方案成为第 $k$ 小，必然是由于 $a[i] + b[j-1]$ 产生了它，往前依次类推必然是在某一时刻选择了 $a[i] + b[0]$，而 $a[i] + b[0]$ 会产生两个候选者 $a[i+1] + b[0]$ 和 $a[i] + b[1]$，由此可知选中方案 $a[i] + b[j]$，只要 $j \ge 1$，那么此时队列里必然曾经出现过 $a[i+1] + b[0]$。

因此，如果说选定 $a[i] + b[j]$ 成为第 $k$ 小同时堆中没有 $a[i+1] + b[j]$，那么此时堆中必然存在 $a[i+1] +b[0],a[i+1] +b[1], \cdots ,a[i+1] +b[j-1]$ 中的某一个。显然，存在比 $a[i+1] + b[j]$ 还小的方案，肯定不会选到 $a[i+1] + b[j]$，因此增加该限定条件不影响算法正确性。

时间复杂度：

由于我们每次获取并删除一个堆顶，最多往堆中插入两个新的元素，因此每一次堆的大小最多增加 $1$，又因为最多只有 $N$ 次出堆操作且堆初始为空，因此堆的规模最大为 $O(n)$。

因此每次push和pop都是 $O(\log n)$ 的复杂度，而最多做 $O(n)$ 次push和pop，因此 $O(n \log n)$ 就能求得两个序列的前 $n$ 小的和。

而对于 $M>2$ 的情况，可以先求出第一个序列和第二个序列的前 $n$ 小的和，作为一个新序列再去和第三个序列求前 $n$ 小的和，以此类推总的时间复杂度为 $O(mn \log n)$。

AC代码：

手写二叉堆版本（500ms）：

#include<cstdio>
#include<iostream>
#include<vector>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int,int> pii;

const int maxm=+;
const int maxn=+;

int m,n;
vector<int> a[maxm];
struct Plan{
    pii ptr;
    bool last; //记录本方案是否是由ptr2++得到的
    int sum;
    Plan(){}
    Plan(int i,int j,pii _ptr,bool _last)
    {
        ptr=_ptr;
        last=_last;
        sum=a[i][ptr.first]+a[j][ptr.second];
    }
}init;

struct Heap
{
    int sz;
    Plan heap[*maxn];
    void up(int now)
    {
        while(now>)
        {
            int par=now>>;
            if(heap[now].sum<heap[par].sum) //子节点小于父节点，不满足小顶堆性质
            {
                swap(heap[par],heap[now]);
                now=par;
            }
            else break;
        }
    }
    void push(const Plan &x) //插入权值为x的节点
    {
        heap[++sz]=x;
        up(sz);
    }
    inline Plan top(){return heap[];}
    void down(int now)
    {
        while((now<<)<=sz)
        {
            int nxt=now<<;
            if(nxt+<=sz && heap[nxt+].sum<heap[nxt].sum) nxt++; //取左右子节点中较小的
            if(heap[now].sum>heap[nxt].sum) //子节点小于父节点，不满足小顶堆性质
            {
                swap(heap[now],heap[nxt]);
                now=nxt;
            }
            else break;
        }
    }
    void pop() //移除堆顶
    {
        heap[]=heap[sz--];
        down();
    }
    void del(int p) //删除存储在数组下标为p位置的节点
    {
        heap[p]=heap[sz--];
        up(p), down(p);
    }
    inline void clr(){sz=;}
}h;

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%d%d",&m,&n);
        for(int i=;i<=m;i++)
        {
            a[i].clear();
            for(int j=,x;j<=n;j++)
            {
                scanf("%d",&x);
                a[i].push_back(x);
            }
            sort(a[i].begin(),a[i].end());
        }

        int i=;
        for(int j=;j<=m;j++,i^=)
        {
            init=Plan(i,j,make_pair(,),);
            h.clr();
            h.push(init);
            a[i^].clear();
            while(h.sz)
            {
                Plan now=h.top(); h.pop();

                a[i^].push_back(now.sum);
                if(a[i^].size()>=n) break;

                if(!now.last && now.ptr.first<n-)
                    h.push(Plan(i,j,make_pair(now.ptr.first+,now.ptr.second),));
                if(now.ptr.second<n-)
                    h.push(Plan(i,j,make_pair(now.ptr.first,now.ptr.second+),));
            }
        }
        for(int k=;k<a[i].size();k++) printf("%d ",a[i][k]);
        printf("\n");
    }
}

优先队列版本（563ms）：

#include<cstdio>
#include<iostream>
#include<vector>
#include<queue>
#include<cstring>
#include<algorithm>
using namespace std;
typedef pair<int,int> pii;

const int maxm=+;
const int maxn=+;

int m,n;
vector<int> a[maxm];
struct Plan{
    pii ptr;
    bool last; //记录本方案是否是由ptr2++得到的
    int sum;
    Plan(){}
    Plan(int i,int j,pii _ptr,bool _last)
    {
        ptr=_ptr;
        last=_last;
        sum=a[i][ptr.first]+a[j][ptr.second];
    }
    bool operator<(const Plan& oth)const{return sum>oth.sum;}
}init;

priority_queue<Plan> Q;

int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%d%d",&m,&n);
        for(int i=;i<=m;i++)
        {
            a[i].clear();
            for(int j=,x;j<=n;j++)
            {
                scanf("%d",&x);
                a[i].push_back(x);
            }
            sort(a[i].begin(),a[i].end());
        }

        int i=;
        for(int j=;j<=m;j++,i^=)
        {
            init=Plan(i,j,make_pair(,),);
            while(!Q.empty()) Q.pop();
            Q.push(init);
            a[i^].clear();
            while(!Q.empty())
            {
                Plan now=Q.top(); Q.pop();

                a[i^].push_back(now.sum);
                if(a[i^].size()>=n) break;

                if(!now.last && now.ptr.first<n-)
                    Q.push(Plan(i,j,make_pair(now.ptr.first+,now.ptr.second),));
                if(now.ptr.second<n-)
                    Q.push(Plan(i,j,make_pair(now.ptr.first,now.ptr.second+),));
            }
        }
        for(int k=;k<a[i].size();k++) printf("%d ",a[i][k]);
        printf("\n");
    }
}