基于mindwave脑电波进行疲劳检测算法的设计(4)

　　上一次的实验做到可以从pc端读取到MindWave传输过来的脑电波原始数据了。

　　我是先定义一个结构体，该结构体对应保存所有能从硬件中取到的原始数据。

 struct FD_DATA
 {
     int battery;//电量
     int poor_signal;//连接质量
     int attention;//专注度
     int meditation;//冥想度
     int raw;//原始数据
     int delta;//δ波段
     int theta;//θ脑波
     int alpha1;//α脑波
     int alpha2;//α脑波
     int beta1;//β脑波
     int beta2;//β脑波
     int gamma1;//γ脑波
     int gamma2;//γ脑波
     int blink;//眨眼强度
 };

　　读取的函数为

 struct FD_DATA FD_GetData(int conID)
 {
     struct FD_DATA data;
     TG_ReadPackets(conID,);//一次读取多个，否则在多线程中会因为某些数据包在缓存中而没有读取
     data.battery=TG_GetValue(conID,TG_DATA_BATTERY);
     data.poor_signal=TG_GetValue(conID,TG_DATA_POOR_SIGNAL);
     data.attention=TG_GetValue(conID,TG_DATA_ATTENTION);
     data.meditation=TG_GetValue(conID,TG_DATA_MEDITATION);
     data.raw=TG_GetValue(conID,TG_DATA_RAW);
     data.delta=TG_GetValue(conID,TG_DATA_DELTA);
     data.theta=TG_GetValue(conID,TG_DATA_THETA);
     data.alpha1=TG_GetValue(conID,TG_DATA_ALPHA1);
     data.alpha2=TG_GetValue(conID,TG_DATA_ALPHA2);
     data.beta1=TG_GetValue(conID,TG_DATA_BETA1);
     data.beta2=TG_GetValue(conID,TG_DATA_BETA2);
     data.gamma1=TG_GetValue(conID,TG_DATA_GAMMA1);
     data.gamma2=TG_GetValue(conID,TG_DATA_GAMMA2);
     data.blink=TG_GetValue(conID,TG_DATA_BLINK_STRENGTH);
     if(data.poor_signal<=)
     {
         ErrorNo=;
         data.poor_signal=;
         return data;
     }
     return data;
 }

　　对于获取数据的时间间隔，就有可能有不同的取法了，理论上是时时刻刻的取值的。但是，这样就太占系统cpu了，那到底是多少时间取一次数据比较好呢，我试着1ms,10ms,100ms,500ms,1s,5s等不同的取数据，然后分析。在TG_BAUD_9600波特率情况下大概每500ms各个值就会有变化。

　　下面这个图是我在100ms取一次数据获得的

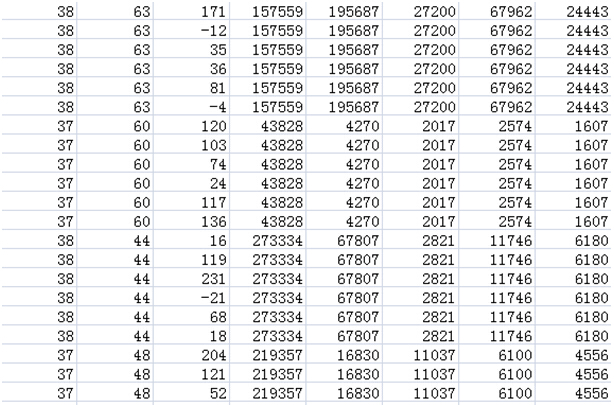
　　分别对应 attention   meditation raw delta  theta  alpha1  alpha2 ... ... 可以可以看到所有有效的数据大概都是5次一次刷新，而其中的raw列就每次都刷新，这个raw波段，我们此次不会涉及到，只是说明每次都是有实际从硬件取到值的。

　　对于取多少比较好呢，我再进行测试的时候是1s取一次。（我觉得如果该算法用于实际，觉得这个取值的时间间隔可以再大一点。）这里我们就会有一个疑问了，每次从硬件中取到的数都不一样，我们1s取一次的话，会不会丢失疲劳信息的有效数据呢。还有就是，按道理人脑是时时刻刻都再发射脑电波的。如果准确的说，1s有无数次采样的话，会有无数种结果。到底为什么可以1s取一次，5s取一次呢？（Ps：这个时间间隔叫做采样间隔）。

　　这个问题困扰我很长时间了，到最近才知道为什么。这个跟时域和频域有关。还有什么傅立叶等等概念有关。

音乐——其实就是时/频分析的一个极好例子，乐谱就是音乐在频域的信号分布，而音乐就是将乐谱变换到时域之后的函数。从音乐到乐谱，是一次傅立叶或小波变换；从乐谱到音乐，就是一次傅立叶或小波逆变换。

　　关于这方面的知识我也似懂非懂的。我也不好解释。反正就是最后对结果的影响不会很大，基本没有影响。还有一点，那个脑电波耳机内部其实还是有做了一些处理的。具体的处理也是上面提到的各种很复杂的级数变换吧。

　　(^-^)?有点跑题了，接下来就是对取到的数据进行绘图分析。为了看图的方便，我这里只画出attention和meditation的曲线，其他的类似。

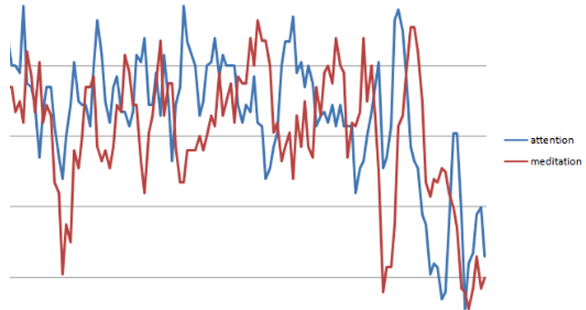
　　我们截取其中的一段，可以看到，这些线波动很大，基本看不到有效的关系。

　　我这里采用两种办法进行预处理。用两种办法是为了反正在进行预处理的时候把有效的信息给处理掉了。所以要两种办法，然后这两种办法再进行一个相关性的假设检验。

　　1.第一种办法是使用常用的办法，就是采用滑动窗口。原理就是这个点的取值是通过计算左右的值的平均值。然后来确定这个值的。这样就能保证是相对稳定的显示了。

　　2.第二种办法是采用自己叫做补偿算法的。原理就是下一个点的值由上一个点来确定，下一个点取当前该点的值减去上一次的值的六十分之一再加上前一个点的值。（思路是这样就能确保每次的增加或减少都是在可控的返回内，每次只是对前一个值的修修补补，不会有大的变化，这一点在接下来的图中可以看出）。还有就是为什么是六十分之一其实百分之一，千分之一。数量级越小，表示受时间影响越大。不同环境该数值应该不同。

　　第二种办法作用是检验attention和meditation在滑动窗口和补偿算法中是否有显著性相关，我们采用 基于成对数据的假设检验(t检验)，来确定滑动窗口这个算法对数据的预处理的有效的，并不会破坏数据的有效信息。如果有显著性相关的话就说明第一种办法是可行的，那么，以后的处理就可以这是一种方法的预处理就可以了。

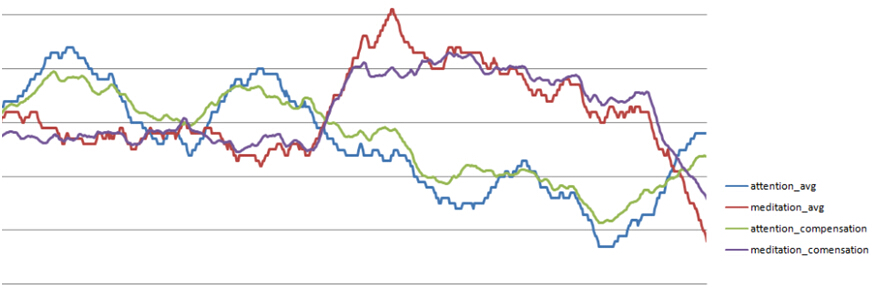
　　得到的是这样的效果，分别是attention两条曲线，meditation两条曲线。这样看就比较正常了，不像上面那样没有规律。我们这样一眼望过去就可以知道两种办法取得的曲线是有点相关性的。作为一个专业的人来说，仅仅靠目测法是不行的。我们要怎样解决呢？这里就要用到t检验了。这个是概率论与数理统计方面的。这个课是大二学的，具体的都忘了，当时也没有怎么认真的学。现在看到这个问题就后悔当初没有认真听课了。（这里插一句，不能不想起当年大一的时候一个ACM的师兄说的一句话“你们是不是觉得大学的高数学了没有用，那是你们还没有到用到它的水平。”当时的理解是这是一个学霸师兄赤果果的嘲讽。现在想想也是有道理的。那个线性代数我是学那个矩阵快速幂算法的时候有用到，而这里的t检验是第一次实际例子中用到数理统计的。而前面提到的傅立叶是在高数中有提到的。如果时间可以倒流，回到那个时候，你还会不会认真的对待这些数学。我肯定的回答，应该还是不会。）

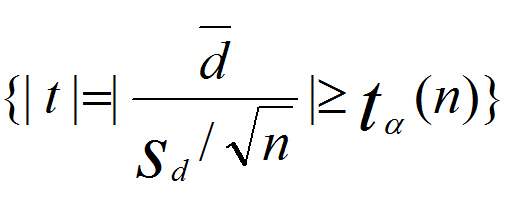
　　d’是样本均值 Sd是样本方差 n是样本个数  α是置信区间 具体其他的就自己看书了。

　　还是给出代码比较好理解吧

 //基于成对数据的假使检验
 double FD_t_check_pair(double * x,double * y,int size)
 {
     double * d;
     double avg=0.0;//用于计算平均数
     double sd=0.0;//用于保存方差
     int i,j;
     d=(double *)malloc(size*sizeof(double));
     for(i=;i<size;i++)
     {
         d[i]=x[i]-y[i];
         avg=avg+d[i];
     }
     avg=avg/size;
     sd=0.0;
     for(i=;i<size;i++)
     {
         sd=sd+((avg-d[i])*(avg-d[i]));
     }
     sd=sd/(size-);
     printf("sd=%lf\n",sd);
     double t;
     t=fabs(avg/(sd/sqrt(size)));
     free(d);
     return t;
 }

　　我得出的结论是在置信区间a=0.025 n=500 是attention和meditation对应的t值都是小于2.4的，说明观察值|t| 不落在拒绝域内，故接受H假使，认为使用两种预处理得到的结果无显著差异。

　　好了，这一节就到这里了，有什么错误欢迎指出。下一节将讲述 αβθ之间的关系，对人体的疲劳状态是否有明显的相关性。这一步将通过这些关系与硬件提供的attention值和meditation值进行相关性检验，来确定硬件给出的值是否有效，还有通过对人的具体实验进行分析。总体代码现在比较乱，就先不给出了，等以后有机会整理完再发吧。

　　参考资料：

　　　　概率论与数理统计及其应用 (高等教育出版社)  (盛 骤  谢式千)

　　　　还有一个音乐的例子，网上都是写转载，但没有给出出处，我就不好写了。

　　本文链接：http://www.cnblogs.com/wunaozai/p/3766779.html